§6.6二阶常系数非齐次线性微分方程 概念 解的 主要 结构 内容 解法
主要 内容 概念 解的 结构 解 法 §6.6 二阶常系数非齐次线性微分方程

二阶常系数非齐次线性微分方程的定义 定义1:形如y"+py'+y=f(x)(1) y"+py'+qy=O (2) 的方程叫做二阶常系数非齐次线性 称为二阶常系数非齐次线性 微分方程.其中P,q为常数,f(x)丰0. 微分方程()对应的齐次方程 课堂训练1:下列是二阶非齐次线性方程的是() (1) dy_dy=I (2) (3) d'y +y=0 dx2 dx dy_dy+y=x dx (4) d'y dr?-x -+y=0 (5) dy_3dy+4y=x (6)y”+2y=0 dx dx
一、 二阶常系数非齐次线性微分方程的定义 定义 1:形如 y py qy f x ( ) (1) 的方程叫做二阶常系数非齐次线性 微分方程其中 p q, 为常数, f (x) 0. 课堂训练 1:下列是二阶非齐次线性方程的是( ) (1) 1 2 2 dx dy dx d y (2) y x dx dy dx d y x 2 2 (3) 0 2 2 xy dx d y (4) 0 2 2 y dx dy x dx d y (5) y x dx dy dx d y 3 4 2 2 (6) y y 2 0 y py qy 0 (2) 称为二阶常系数非齐次线性 微分方程(1)对应的齐次方程
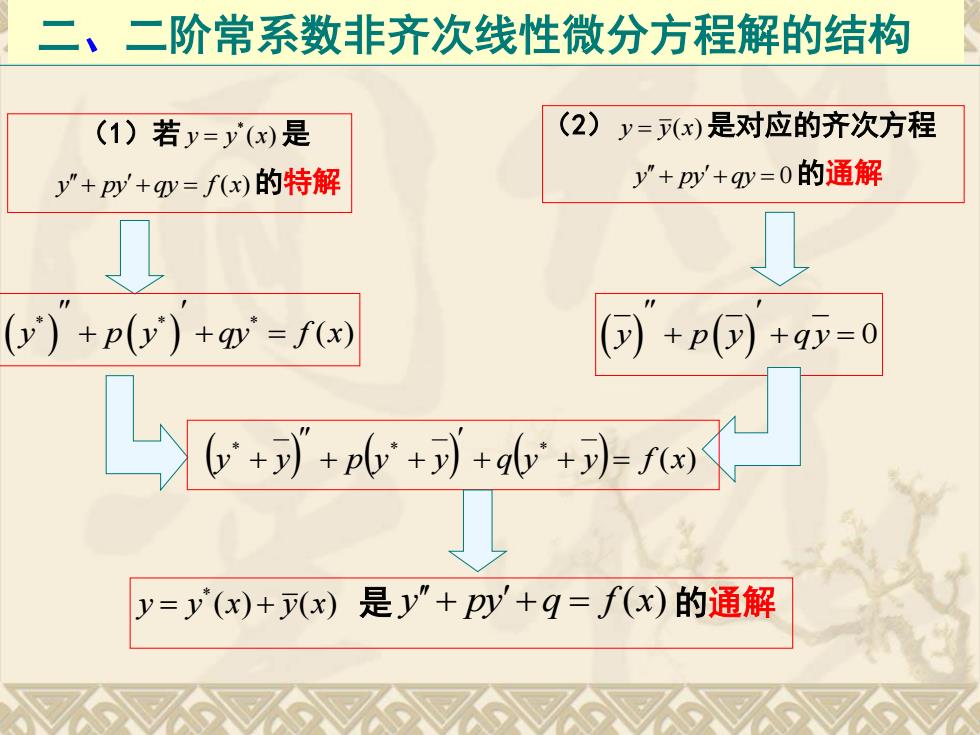
二、二阶常系数非齐次线性微分方程解的结构 (1)若y=y(x)是 (2)y=(x)是对应的齐次方程 y”+py+gy=fx)的特解 y”+py+y=0的通解 (y)+p(y)+p=fx) ⊙)+p()+9=0 +水a y=y(x)+(x)是y”+py+q=f(x)的通解
二、二阶常系数非齐次线性微分方程解的结构 (1)若 * y y x ( )是 y py qy f x ( )的特解 (2) y y x ( )是对应的齐次方程 y py qy 0的通解 * * * y p y qy f x( ) y p y q y 0 ( ) * * * y y p y y q y y f x * y y x y x ( ) ( ) 是 y py q f x ( ) 的通解

二、二阶常系数非齐次线性微分方程解的结构 定理1若y=y(x)是y”+py+y=f(x)的特解 y=(x)是y”+py+缈=0的通解 则y=y(x)+(x)是y”+py+q=f(x)的通解 注记1:求二阶常系数非齐次线性微分方程y”+py+y=f(x) 通解的思路 第一步:求出y”+py+y=0通解y=(x) 第二步:求出y”+py+y=f(x)特解y=y(x) 第三步:求出y”+py'+y=f(x)通解y=(x)+y(x)
定理 1 若 * y y x ( ) 是 y py qy f x ( )的特解 y y x ( ) 是 y py qy 0的通解 则 * y y x y x ( ) ( )是 y py q f x ( ) 的通解 注记 1:求二阶常系数非齐次线性微分方程 y py qy f x ( ) 通解的思路 第一步: 求出 y py qy 0通解 y y x ( ) 第二步: 求出 y py qy f x ( )特解 * y y x ( ) 第三步: 求出 y py qy f x ( ) 通解 * y y x y x ( ) ( ) 二、二阶常系数非齐次线性微分方程解的结构

三、二阶常系数非齐次线性微分方程的特解 定理2:二阶常系数非齐次齐次线性微分方程特解的形式 若f(x)=pn(x)e y”+py+q=f(x)具有下列形式的特解 (1)2不是特征方程的根 (1)y=e(x)e* (2)1是特征方程的单根 (2)y'=xe (x)e (3)1是特征方程的重根 (3)y=x20n(x)e2x f(x)=e (Acosox+Bsin@x) y”+py+q=f(x)具有下列形式的特解 (4)2+io不是特征方程的根 (4)y=eix (acosox+bsin@x) (5)1+io是特征方程的根 (5)y=xe(acosox+bsinox)
三、二阶常系数非齐次线性微分方程的特解 定理 2: 二阶常系数非齐次齐次线性微分方程特解的形式 若 ( ) ( ) x m f x p x e y py q f x ( ) 具有下列形式的特解 (1) 不是特征方程的根 (1) * ( ) x m y Q x e (2) x m y xQ x e ( ) * (2) 是特征方程的单根 (3) 是特征方程的重根 (3) * 2 ( ) x m y x Q x e 若 ( ) cos sin x f x e A x B x y py q f x ( ) 具有下列形式的特解 (4) i不是特征方程的根 (4) cos sin x y e a x b x (5) i是特征方程的根 (5) cos sin x y xe a x b x

三、二阶常系数非齐次线性微分方程的特解 注记2:若f(x)=pm(x)e 注记3:若f(x)=e“(Acos@x+Bsin@x)) 求y”+py+q=f(x)特解的步骤 求y”+py+q=f(x)特解的步骤 1:判断f(x)的类型找出乙,m 1:判断f(x)的类型找出元,o 2:找出入与特征方程的关系 2:找出人+0与特征方程的关系 3:设出该方程的特解表达式 3:设出该方程的特解表达式 4:求出特解表达式中的系数 4:求出特解表达式中的系数
三、二阶常系数非齐次线性微分方程的特解 1:判断 f x( )的类型找出,m 2:找出 与特征方程的关系 第三步: 求出 y py qy f x ( )特解 * y y x y x ( ) ( ) 3:设出该方程的特解表达式 4:求出特解表达式中的系数 注记 2:若 ( ) ( ) x m f x p x e 求 y py q f x ( ) 特解的步骤 2:找出 i 与特征方程的关系 注记 3:若 ( ) cos sin x f x e A x B x 求 y py q f x ( ) 特解的步骤 1:判断 f x( )的类型找出 , 3:设出该方程的特解表达式 4:求出特解表达式中的系数

三、二阶常系数非齐次线性微分方程的特解 例求y-2y-3y=3x+1的一个特解.(1)f(x)=2e是 型,m=0, 解:显然f(x)=3x+1是pn(x)e型 1=_不是2y+y-y=0的特征方程 m=1,元=0 的 根, y"-2y-3y=0的特征方程为 因此2y+y+y=2e*的特解应设 x2-2r-3=0 为y(x)= 显然1=0不是特征方程的根, (2)f(x)=3xex是 型,m=1, 所以原方程的特解为y(x)=bx+b, =是y”+3y+2y=0的特 代入可得-2b,-3(bx+b)=3x+1 征方程 的根 比较两端x同次幂的系数得一弘=3 1-2b-3h=1 因此y"+3y+2y=3xe的特解应 由此求得6,=-1,h=故y(x)=-x+ 设为y(x)=
三、二阶常系数非齐次线性微分方程的特解 例 求 y y y x 2 3 3 1的一个特解 解:显然 f x x ( ) 3 1 是 ( ) x m p x e 型 m 1, 0 y y y 2 3 0的特征方程为 2 r r 2 3 0 显然 0 不是特征方程的根 所以原方程的特解为 * 0 1 y x b x b ( ) 代入可得 0 0 1 2 3( ) 3 1 b b x b x 比较两端x同次幂的系数得 2 3 1 3 3 0 1 0 b b b 由此求得 0 1 1 1, 3 b b 故 * 1 ( ) 3 y x x (1) ( ) 2 x f x e 是 型, m 0, __不是2 0 y y y 的特征方程 的 根, 因此2 2 x y y y e 的特解应设 为 * y x( ) ________ _ ____ (2) ( ) 3 x f x xe 是 型, m 1, _ 是 y y y 3 2 0的特 征方程 的 根, 因此 3 2 3 x y y y xe 的特解应 设为 * y x( ) __________ ____

三、二阶常系数非齐次线性微分方程的特解 3)f(x)=(x+1)e3x是 型,m=1, 因此y"+3y+2y=e-*cosx的特解 1=是y-6y+9y=0的特征方程 应设为y(x)= 的 根, (5)f(x)=3cosx+sinx是 型, 因此y"-6y+9y=(x+1)e3x的特解 w= 显然九+w是 应设为y(x)= y+y=0的特征方程的特征根, (4)f(x)=e-*cosx是 型, =一,w=,显然+w不是 因此y”+y=3cosx+sinx的特解应 y”+3y+2y=0的特征方程的特征根, 设为y(x)=
三、二阶常系数非齐次线性微分方程的特解 (3) 3 ( ) 1 x f x x e 是 型,m 1, __是 y y y 6 9 0的特征方程 的 根, 因此 3 6 9 1 x y y y x e 的特解 应设为 * y x( ) _______ _ ____ (4) ( ) cos x f x e x 是 型, ____,w ____,显然 iw不是 y y y 3 2 0的特征方程的特征根, 因此 3 2 cos x y y y e x 的特解 应设为 * y x( ) ______ _____ (5) f x x x ( ) 3cos sin 是 型, ____,w ____,显然 iw是 y y 0的特征方程的特征根, 因此 y y x x 3cos sin 的特解应 设为 * y x( ) _________ _____ 设为 * y x( ) _________ _____