
§7.7空间曲线及其方程 空间曲线 的一般方程 空间曲线在 空间曲面 坐标面上的投 在坐标面上的 影 投影 空间曲线 的参数方程 OoOD⊙⑧ 凯机动
机动 目录 上页 下页 返回 结束 §7.7 空间曲线及其方程 空间曲线 的一般方程 空间曲线 的参数方程 空间曲线在 坐标面上的投 影 空间曲面 在坐标面上的 投影
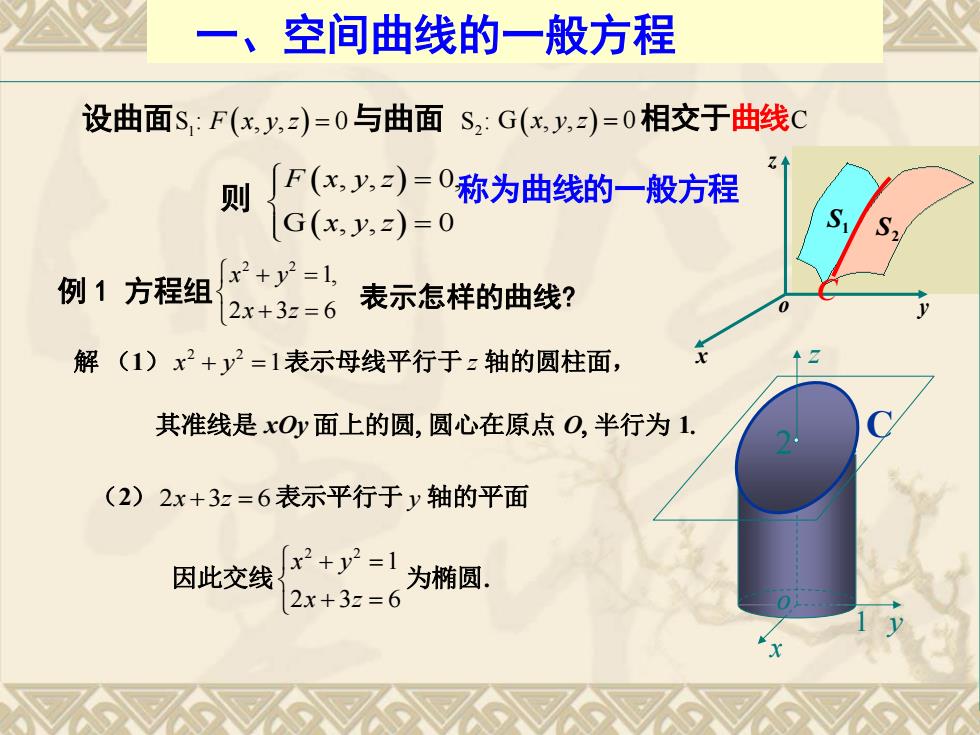
一、空间曲线的一般方程 设曲面S:F(x,y,)=0与曲面S2:G(x,y,)=0相交于曲线C 则 ∫F(x,y,)=0称为曲线的一般方程 G(x,y,z)=0 S S2 例1方程组 2+y=1 2x+3z=6 表示怎样的曲线? 解(1)x2+y2=1表示母线平行于z轴的圆柱面, 其准线是xOy面上的圆,圆心在原点O,半行为1, (2)2x+3z=6表示平行于y轴的平面 因此交线 x2+y2=1 为椭圆。 2x+3z=6
设曲面S:1 F x y z , , 0 与曲面 , , 0, G , , 0 F x y z x y z 称为曲线的一般方程 一、空间曲线的一般方程 则 S:2 G , , 0 x y z 相交于曲线C x o z y S1 S2 例 1 方程组 C 2 2 1, 2 3 6 x y x z 表示怎样的曲线 ? 解 (1) 1 2 2 x y 表示母线平行于 z 轴的圆柱面, 其准线是 xOy 面上的圆 圆心在原点 O 半行为 1 (2)2x 3z 6表示平行于 y 轴的平面 因此交线 2 3 6 1 2 2 x z x y 为椭圆. x z 1 y o C 2

一、空间曲线的一般方程 1.方程组 表示怎样的曲线? z=va2-x2-y 2.方程组 +广=R: 表示怎样的曲线? x2+22=R2 3.方程组 x2+y2+z2=4a 表示怎样的曲线? x2+y2-2ax=0 4.方程组 表示怎样的曲线? z=2-x2-y
1. 方程组 2 2 2 2 2 2 2 2 a a x y z a x y 表示怎样的曲线? 一、空间曲线的一般方程 2. 方程组 2 2 2 2 2 2 x y R x z R 表示怎样的曲线? 3. 方程组 2 2 2 2 2 2 4 2 0 x y z a x y ax 表示怎样的曲线? 4. 方程组 2 2 2 2 2 z x y z x y 表示怎样的曲线?

二、空间曲线的参数方程 将曲线C上的动点的坐标x,y,z表示为参数1的函数: x=x(t) y=y(t) 当给定1=t时,就得到C上的一个点(x,y,) z=2(t) 随着的变动就得到曲线C上的全部点 联想圆的 空间曲线的 例2求曲线 的参数方程 参数方程! 参数方程。 (z=Va2-x2-y2 解设x-号 n0,即x=cos,y=号n0 a cose,y= a a 2 代入球面方程得 =dsin 0 x=a+acos0 22 a y-2sine (0≤0≤2π) 于是所求曲线的参数方程为 -asin
将曲线C 上的动点的坐标x y z , , 表示为参数t 的函数: 二、空间曲线的参数方程 ( ) ( ) ( ) z z t y y t x x t 当给定 1 t t 时,就得到C 上的一个点 x y z 1 1 1 , , 随着t的变动就得到曲线C 上的全部点. 空间曲线的 例 2 求曲线 参数方程. 2 2 2 2 2 2 2 2 a a x y z a x y 的参数方程. 解 设 cos , sin 2 2 2 a a a x y ,即 cos , sin 2 2 2 a a a x y 代入球面方程得 sin . 2 z a 于是所求曲线的参数方程为 cos 2 2 sin (0 2 ). 2 sin 2 a a x a y z a 联想圆的 参数方程

二、空间曲线的参数方程 圆柱螺旋线的参数方程为 x=acos ot, 令0=oL,b=y x=acos0 y=asin ot, 0 y=asin z=bot 螺旋线上升的高度与转过的角度成正比 z=b0 1.试写出曲线 x2+y=3 的参数方程 z=0 2.试写出曲线 Y-少=1的参数方程 z=1 2.试写出曲线 x+y+=3 的参数方程 x=y
二、空间曲线的参数方程 圆柱螺旋线的参数方程为 z b t y a t x a t sin , cos , 令 v t, b z b y a x a sin cos 螺旋线上升的高度与转过的角度成正比 1.试写出曲线 2 2 2 3 0 x y z 的参数方程 2.试写出曲线 2 2 1 1 x y z 的参数方程 2.试写出曲线 2 2 2 2 x y z 3 x y 的参数方程

三、空间曲线在坐标面上的投影 将空间曲线的一般方程: F(x,y,z)=0 依次消去一元,可得 G(x,y,z)=0 F(x,y)=0 F(y,)=0 F(x,)=0 空间曲线对xoy面 空间曲线对y0oz面 空间曲线对xoz面 的投影柱面 的投影柱面 的投影柱面 E(x,y)=0 F(y,z)=0 F(x,2)=0 z=0 x=0 y=0 空间曲线对xoy面 空间曲线对y0z面 空间曲线对x0z面 的投影曲线 的投影曲线 的投影曲线
将空间曲线的一般方程: ( , , ) 0 ( , , ) 0 G x y z F x y z 依次消去一元,可得 三、空间曲线在坐标面上的投影 1 F x y ( , ) 0 2 F y z ( , ) 0 3 F x z ( , ) 0 空间曲线对xoy 面 的投影柱面 1 ( , ) 0 0 F x y z 2 ( , ) 0 0 F y z x 3 ( , ) 0 0 F x z y 空间曲线对 yoz 面 的投影柱面 空间曲线对xoz 面 的投影柱面 空间曲线对xoy 面 的投影曲线 空间曲线对 yoz 面 的投影曲线 空间曲线对xoz 面 的投影曲线

三、空间曲线在坐标面上的投影 注记:求空间曲线 F(x,y,2)=0 在坐标面上投影方程的一般步骤 G(x,y,z)=0 第一步:在 F(x,y,2)=0 中分别消去x,y,z得到该曲线关于三坐标 G(x,y,z)=0 面的投影柱面方程 第二步:将坐标面的投影柱面方程与该坐标面的方程联立可得 空间曲线在坐标面上的投影曲线的方程 x2+y2+z2=1 例3求曲线C: 在yOz面及上Oy面上的投影 x2+(0y-102+(2-1)2=1
注记 :求空间曲线 ( , , ) 0 ( , , ) 0 G x y z F x y z 在坐标面上投影方程的一般步骤 三、空间曲线在坐标面上的投影 第一步:在 ( , , ) 0 ( , , ) 0 G x y z F x y z 中分别消去 x, y,z得到该曲线关于三坐标 面的投影柱面方程 第二步:将坐标面的投影柱面方程与该坐标面的方程联立可得 空间曲线在坐标面上的投影曲线的方程 例 3 求曲线 ( 1) ( 1) 1 1 : 2 2 2 2 2 2 x y z x y z C 在 yoz 面及上 xoy 面上的投影
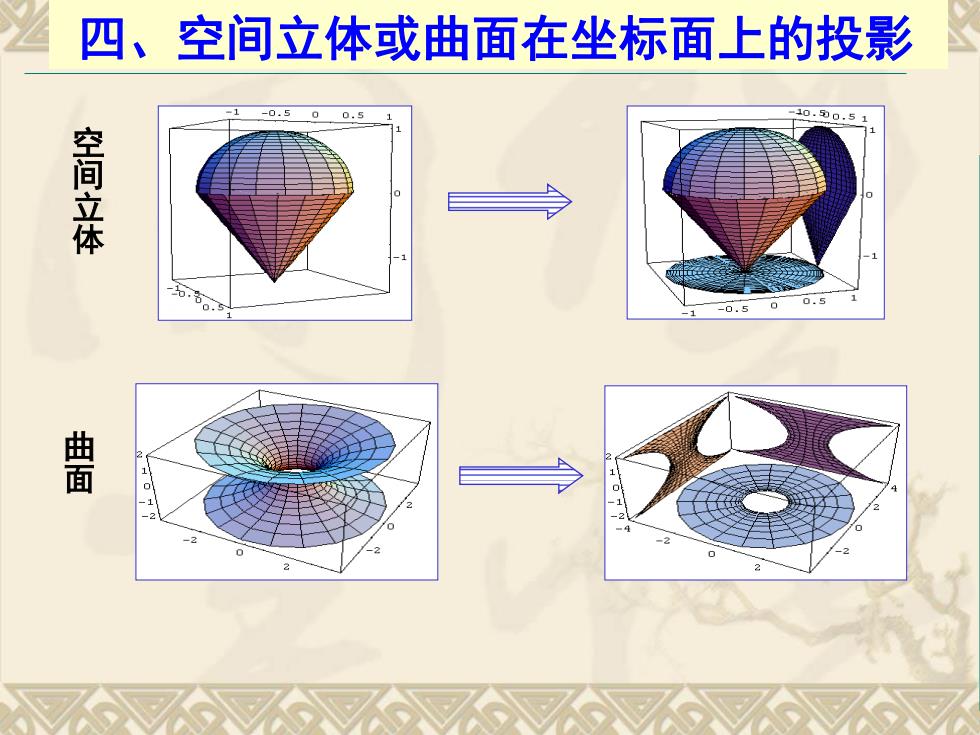
四、空间立体或曲面在坐标面上的投影 0.5 0.5 空间立体 0.5 0.5 曲面
四、空间立体或曲面在坐标面上的投影 空 间 立 体 曲 面

四、空间立体或曲面在坐标面上的投影 例4求由上半球面z=√4-x2-y2和锥面z=V3(x2+y2)围成 的立体在xoy面上的投影, 解半球面和锥面的交线为C: 2=4-x2-y2 2=V3x2+y) 消去z得投影柱面x2+y2=1,则交线C在xOy面上的投影为圆 x2+y2=1 z=0 所求立体在xoy面上的投影为x2+y2≤1
例 4 2 2 求由上半球面 z 4 x y 和锥面 3( ) 2 2 z x y 围成 的立体在 xoy面上的投影. 解 半球面和锥面的交线为 3( ), 4 , : 2 2 2 2 z x y z x y C 1, 2 2 消去 z 得投影柱面 x y 则交线C 在 xoy 面上的投影为圆 0. 1, 2 2 z x y 所求立体在 xoy 面上的投影为 1. 2 2 x y 四、空间立体或曲面在坐标面上的投影

课题训练 1.试写出半球面x2+y2+z2≤a2,z≥0在x0y面上的投影曲线方程 2. 试写出=+r 在xoy面上的投影曲线方程 z=2-x2-y2 3.试写出+广+=4在o面上的投影曲线方程 x2+y2-2ax=0 写出仁在面上的投影抽蛙方程 4.ì
1.试写出半球面 2 2 2 2 x y z a z , 0 在 xoy面上的投影曲线方程 课题训练 2. 试写出 2 2 2 2 2 z x y z x y 在 xoy面上的投影曲线方程 3. 试写出 2 2 2 2 2 2 4 2 0 x y z a x y ax 在 xoy面上的投影曲线方程 4. 试写出 2 2 2 2 2 2 x y R x z R 在xoy面上的投影曲线方程