§10.4函数张开成幂级数 将函数展开成幂级数的背景 主要内容 将国数展成幂级数的条件 将函数展开成幂级数的步骤
§10.4 函数张开成幂级数 将函数展开成幂级数的背景 将函数展成幂级数的条件 主 要 内 容 将函数展开成幂级数的步骤

函数展成幂级数的背景 问 题 计算机是如何计算sinx的函数值的? 函数f(x)在含有x,的开区间内具有直到n+I阶导数, 近似计算 我们希望做找出一个关于x一x,的n次多项式P(x) f(x)≈f(xo)+f"(xx-x) P(x)=ao+a(x-xo)+a(x-xo)2+...a(x-xp)2 误差为 R(x)=f(x)-f(xo)+f(xo)(x-xo)=o(x-xo) 使得 fx)≈P(x) 这种近似表达式精确度不高.作近似计算时 R(x)=f(x)-P.(x)→0(n→0) 不能具体估算出误差大小.为了达到一定精确度显然(1)P(x)就是幂级数的前项部分和s,(x). 的要求,可考虑用n次多项式P(x)近似f(x) (2)R(x)就是幂级数余项(x)
一、 函数展成幂级数的背景 问 题 计算机是如何计算sin x 的函数值的? 近似计算 0 0 0 f x f x f x x x ( ) ( ) ( )( ) 误差为 0 0 0 0 R x f x f x f x x x o x x ( ) ( ) ( ) ( )( ) ( ) 这种近似表达式精确度不高. 作近似计算时 不能具体估算出误差大小为了达到一定精确度 的要求 可考虑用n 次多项式 ( ) P x n 近似 f x( ) 函数 f x( )在含有 0 x 的开区间内具有直到n 1阶导数 我们希望做找出一个关于 0 x x 的n 次多项式 ( ) P x n 2 2 0 1 0 2 0 0 ( ) ( ) ( ) ( ) P x a a x x a x x a x x n n 使得 ( ) ( ) n f x P x ( ) ( ) ( ) 0 ( 0) R x f x P x n n n 显然(1) ( ) P x n 就是幂级数的前 n 项部分和 ( ) n s x . (2) ( ) R x n 就是幂级数余项 ( ) n r x
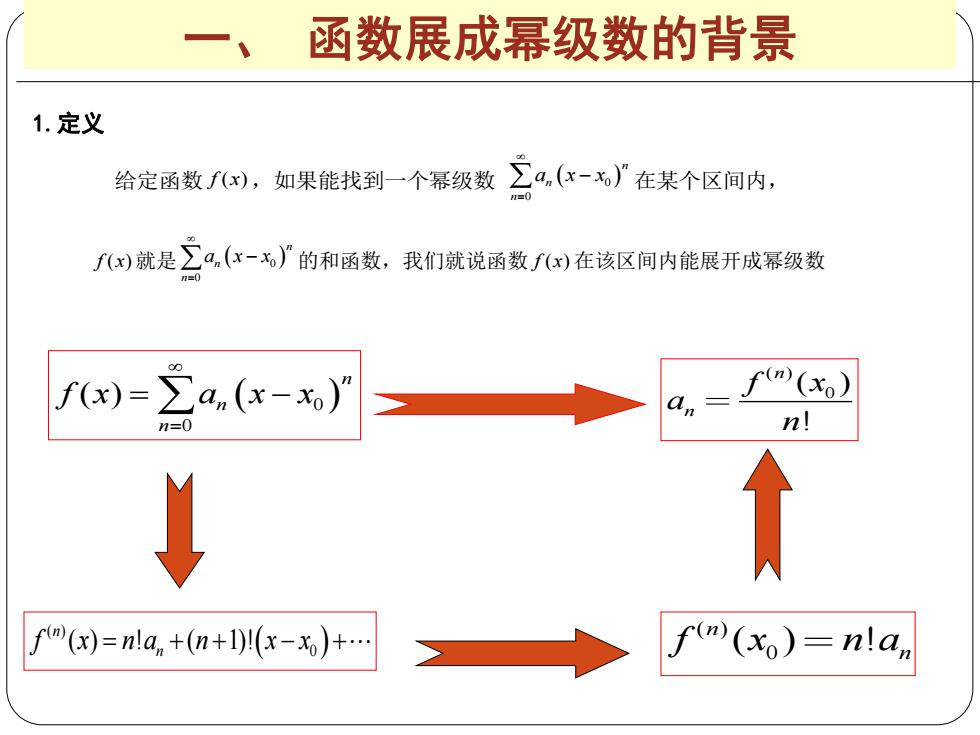
函数展成幂级数的背景 1.定义 给定函数f(x),如果能找到一个幂级数 立a,x-)广在某个区间内, f就是立a,(x-x)的和函数,我们就说函数()在该区间内能展开成幂级数 n fw)=2a.(x-) 0 f”(x) an n=0 n! f(x)=nla,+(n+1)!(x-x)+ f(m(x)=n!an
一、 函数展成幂级数的背景 1.定义 给定函数 f x( ),如果能找到一个幂级数 0 0 n n n a x x 在某个区间内, f x( )就是 0 0 n n n a x x 的和函数,我们就说函数 f x( ) 在该区间内能展开成幂级数 0 0 ( ) n n n f x a x x ( ) 0 ( ) ! ( 1)! n n f x n a n x x ( ) 0 ( ) ! n n f x n a ( ) 0 ( ) ! n n f x a n

二、 函数展成幂级数的条件 1.函数能展开成幂级数的必要条件 2.泰勒级数与麦克劳林级数 如果函数f(x)在含有x,的某邻域内 如果函数f(x)在含有x的某邻域内任意阶可导, 能展开成 侧幂级数-就称为函数)布 n! 幂级数∑a(x-x)》,则 点x处泰勒级数 0 寡级数之(-广就称为函数f八田在 n! f((xo) n=0,1,2… n! 点,=0处麦克劳林级数 注记1:西数在点气处素到极数交。-厂不一定收数于了
二、 函数展成幂级数的条件 1.函数能展开成幂级数的必要条件 2.泰勒级数与麦克劳林级数 如果函数 f x( )在含有 0 x 的某邻域内 幂级数 0 0 n n n a x x ,则 ( ) 0 ( ) , 0,1,2 ! n n f x a n n 则幂级数 ( ) 0 0 0 ( ) ! n n n f x x x n 就称为函数 f x( ) 在 如果函数 f x( )在含有 0 x 的某邻域内任意阶可导, 点 0 x 处泰勒级数 幂级数 ( ) 0 0 0 ( ) ! n n n f x x x n 就称为函数 f x( ) 在 点 0 x 0处麦克劳林级数 能展开成 注记 1:函数 f x( )在点 0 x 处泰勒级数 ( ) 0 0 0 ( ) ! n n n f x x x n 不一定收敛于 f x( )

二、函数展成幂级数的条件 3.函数能展开成幂级数的充分条件 (1)如果函数f(x)在含有x的某邻域 即 空-r-a. 内任意阶可导 R网--- (2) lim R,(x)=0 1→g0 则函数f(x)可以展开成幂级数 R但(x-“称为拉格朗日余项 (n+1)! - R=a包x“ (n+1)! 称为麦克劳林余项
二、 函数展成幂级数的条件 3.函数能展开成幂级数的充分条件 (2) lim ( ) 0 n n R x (1)如果函数 f x( ) 在含有 0 x 的某邻域 内任意阶可导 则函数 f x( )可以展开成幂级数 ( ) 0 0 0 ( ) ! n n n f x x x n . ( ) 0 0 0 ( ) ( ) ( ) ! n i i i n f x x x i R x f x ( 1) 1 0 ( ) ( ) ( 1)! n n n f R x x x n 称为拉格朗日余项 ( 1) 1 ( ) ( ) ( 1)! n n n f R x x n 称为麦克劳林余项 即 ( ) 0 0 0 ( ) ( ) ! n n n f x x x f x n

三、 函数展成幂级数的步骤 1.求函数能展开成麦克劳林级数的步骤 第一步:求f(x)在x=0的处的各阶导数f(O) 第二步:写出f(x)的麦克劳林级数并求其收敛区间 (2)n x∈(-0,+0) 第三步:验证在收敛区间内 2-yew 1=0 lim R (x)=lim f+(00x1=0 n→两(n+1)! e-r on! x∈(-0,t0) n(1+--Ix x∈(-1,1] n=l n 0 sinx= 、(-1) (2k+1)川 x∈(-00,+o0) arctan x∈[-1,1] 2n+1
三、 函数展成幂级数的步骤 1.求函数能展开成麦克劳林级数的步骤 第一步:求 f x( )在 x 0的处的各阶导数 ( ) (0) k f 第三步:验证在收敛区间内 ( 1) 1 ( ) lim ( ) lim 0 ( 1)! n n n n n f x R x x n 第二步:写出 f x( )的麦克劳林级数并求其收敛区间 0 ! n x n x e n = x ( , ) 2 1 0 ( 1) sin 2 1 !! k k k x x k = x ( , ) 0 1 ( 1) 1 n n n x x = x ( 1,1) 2 0 ( 1) cos 2 !! k k k x x k = x ( , ) 2 2 0 1 ( 1) 1 n n n x x = x ( 1,1) 1 1 ( 1) ln 1 n n n x x n = x ( 1,1] 2 1 0 ( 1) arctan 2 1 n n n x x n = x [ 1,1]
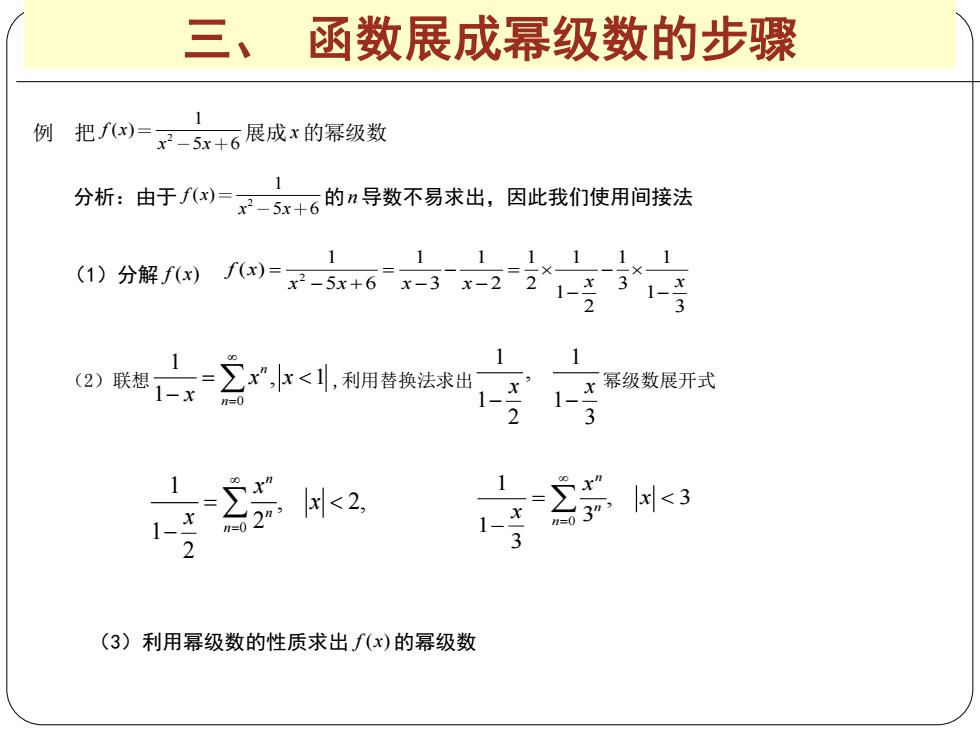
三、函数展成幂级数的步骤 例 把)=F-5x十6展成x的幂级数 分析:由于心)F一5x+6的n导数不易求出,因此我们使用间接法 1 11111 (1)分解fx)f(x)=x2-5x+6x-3x-22 1-x3 1、x 1 1 (2)联想 幂级数展开式 3 1 2 <2, 1 I_r 03 x<3 (3)利用幂级数的性质求出f(x)的幂级数
三、 函数展成幂级数的步骤 例 把 2 1 ( ) 5 6 f x x x 展成 x 的幂级数 分析:由于 2 1 ( ) 5 6 f x x x 的n 导数不易求出,因此我们使用间接法 (1)分解 f x( ) 2 1 1 1 1 1 1 1 ( ) 5 6 3 2 2 3 1 1 2 3 f x x x x x x x (2)联想 0 1 , 1 1 n n x x x ,利用替换法求出 1 1 , 1 1 2 3 x x 幂级数展开式 0 1 , 2, 2 1 2 n n n x x x (3)利用幂级数的性质求出 f x( ) 的幂级数 0 1 , 3 3 1 3 n n n x x x