
第五讲 对称特征值问题 1 Jacobi迭代方法 2 Rayleigh商迭代方法 3 对称QR迭代方法 4 分而治之法 5 对分法和反迭代 6 奇异值分解 7 扰动分析 现代数位分析(数值线性代数),潘建瑜 http://math.ecnu.edu.cn/~jypan
第五讲 对称特征值问题 1 Jacobi 迭代方法 2 Rayleigh 商迭代方法 3 对称 QR 迭代方法 4 分而治之法 5 对分法和反迭代 6 奇异值分解 7 扰动分析 现代数值分析(数值线性代数), 潘建瑜 http://math.ecnu.edu.cn/~jypan

秦 4 分而治之法 分而治之法由Cuppen于1981年首次提出,但直到1995年才出现稳定的实现 方式,是目前计算所有特征值和特征向量的最快算法. 考虑不可约对称三对角矩阵 b1 am-1 bm-1 bm-1 am bm T= bm am+1 bm+1 bm+1 bn-1 bn-1 an http://math.ecnu.edu.cn/~jypan 18/77
4 分而治之法 分而治之法由 Cuppen 于 1981 年首次提出, 但直到 1995 年才出现稳定的实现 方式, 是目前计算 所有特征值和特征向量 的最快算法. 考虑不可约对称三对角矩阵 T = a1 b1 b1 . . . . . . . . . am−1 bm−1 bm−1 am bm bm am+1 bm+1 bm+1 . . . . . . . . . . . . bn−1 bn−1 an http://math.ecnu.edu.cn/~jypan 18/77
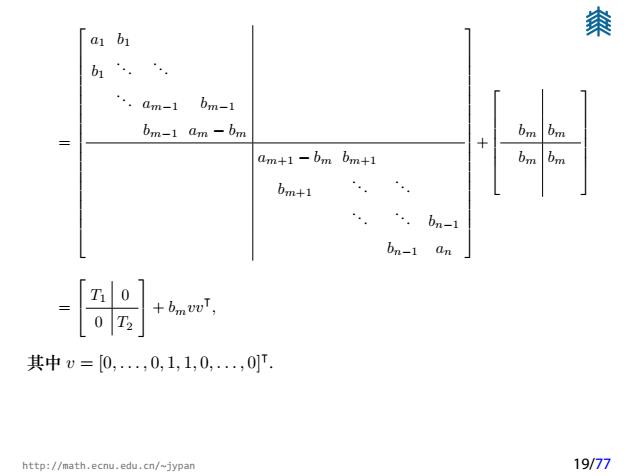
秦 b1 am-1 bm-1 bm-1 am-bm bm bm am+1-bm bm+1 bm bm bm+1 bn-1 bn-1 an 0 +bmwv, 其中v=[0.,0,1,1,0,.,0]T http://math.ecnu.edu.cn/~jypan 19/77
= a1 b1 b1 . . . . . . . . . am−1 bm−1 bm−1 am − bm am+1 − bm bm+1 bm+1 . . . . . . . . . . . . bn−1 bn−1 an + bm bm bm bm = T1 0 0 T2 + bmvv ⊺ , 其中 v = [0, . . . , 0, 1, 1, 0, . . . , 0]⊺ . http://math.ecnu.edu.cn/~jypan 19/77

秦 假定T1和T2的特征值分解已经计算出来 即T=Q1△1Q1,T2=Q2A2Q2,下面考虑T的特征值分解. T 0 T QiAIQI 0 0T2 0 Q242Q5 -ed网e 其中 - Q1的最后一列 令a=bm,D=diag(A1,A2)=diag(d1,d2,.,dn),并假定d1≥d2≥…≥dn. 则T的特征值与D+auuT的特征值相同. http://math.ecnu.edu.cn/~jypan 20/77
假定 T1 和 T2 的特征值分解已经计算出来 即 T1 = Q1Λ1Q ⊺ 1 , T2 = Q2Λ2Q ⊺ 2 , 下面考虑 T 的特征值分解. T = T1 0 0 T2 + bmvv ⊺ = Q1Λ1Q ⊺ 1 0 0 Q2Λ2Q ⊺ 2 + bmvv ⊺ = Q1 0 0 Q2 Λ1 0 0 Λ2 + bmuu ⊺ Q1 0 0 Q2 ⊺ , 其中 u = Q1 0 0 Q2 ⊺ v = Q ⊺ 1 的最后一列 Q ⊺ 2 的第一列 . 令 α = bm, D = diag(Λ1,Λ2) = diag(d1, d2, . . . , dn), 并假定 d1 ≥ d2 ≥ · · · ≥ dn. 则 T 的特征值与 D + αuu ⊺ 的特征值相同. http://math.ecnu.edu.cn/~jypan 20/77

秦 考虑D+auuT的特征值 设入是D+au「的一个特征值,若D一入I非奇异,则 det(D+auuT-入I)=det(D-入I)·det(I+a(D-λI)-1uu) 故det(I+a(D-λI)-1uuT)=0. 引理设x,y∈R”,则det(I+xy)=1+yx. 于是 det(I+a(D-X))=1+ou(D-u=1+a 台4-入 f) 故求A的特征值等价于求特征方程f(入)=0的根。 http://math.ecnu.edu.cn/-jypan 21/77
考虑 D + αuu ⊺ 的特征值 设 λ 是 D + αuu ⊺ 的一个特征值, 若 D − λI 非奇异, 则 det(D + αuu ⊺ − λI) = det(D − λI) · det(I + α(D − λI) −1uu ⊺ ). 故 det(I + α(D − λI) −1uu ⊺ ) = 0. 引理 设 x, y ∈ R n , 则 det(I + xy ⊺ ) = 1 + y ⊺ x . 于是 det(I + α(D − λI) −1uu ⊺ ) = 1 + αu ⊺ (D − λI) −1u = 1 + α Xn i=1 u 2 i di − λ ≜ f(λ) 故求 A 的特征值等价于求特征方程 f(λ) = 0 的根. http://math.ecnu.edu.cn/~jypan 21/77
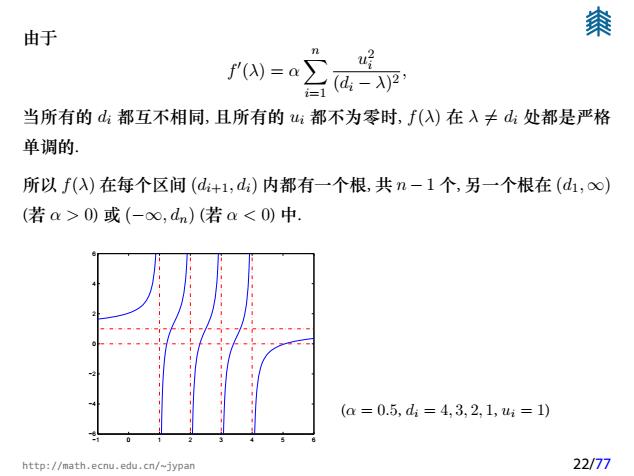
由于 秦 u? ) 当所有的d山都互不相同,且所有的都不为零时,f()在入卡d山:处都是严格 单调的。 所以f()在每个区间(d+1,d)内都有一个根,共n-1个,另一个根在(d1,0o) (若a>0)或(-o,dn)(若a<0)中. (a=0.5,d:=4,3,2,1,u=1) http://math.ecnu.edu.cn/~jypan 22/77
由于 f ′ (λ) = α Xn i=1 u 2 i (di − λ) 2 , 当所有的 di 都互不相同, 且所有的 ui 都不为零时, f(λ) 在 λ ̸= di 处都是严格 单调的. 所以 f(λ) 在每个区间 (di+1, di) 内都有一个根, 共 n − 1 个, 另一个根在 (d1, ∞) (若 α > 0) 或 (−∞, dn) (若 α < 0) 中. −1 0 1 2 3 4 5 6 −6 −4 −2 0 2 4 6 (α = 0.5, di = 4, 3, 2, 1, ui = 1) http://math.ecnu.edu.cn/~jypan 22/77

秦 由于f(A)在每个区间(d+1,d)内光滑且严格单调递增(a>0)或递减(a<0), 所以在实际计算中,可以使用对分法,牛顿法及其变形,或有理逼近等算法来求 解.通常都能很快收敛,一般只需迭代几步即可 因此,计算一个特征值的运算量约为O(n),计算D+auu'的所有特征值的运 算量约为0(n2). 当所有特征值计算出来后,我们用下面的引理来计算特征向量. 引理设D∈Rnxn为对角矩阵,u∈R”,a∈R,若入是D+auuT的特征值, 且入≠d,i=1,2,,n,则(D-入I)-1u是其对应的特征向量 (板书) http://math.ecnu.edu.cn/~jypan 23/77
由于 f(λ) 在每个区间 (di+1, di) 内光滑且严格单调递增 (α > 0) 或递减 (α < 0), 所以在实际计算中, 可以使用对分法, 牛顿法及其变形, 或有理逼近等算法来求 解. 通常都能很快收敛, 一般只需迭代几步即可. 因此, 计算一个特征值的运算量约为 O(n), 计算 D + αuu ⊺ 的所有特征值的运 算量约为 O(n 2 ). 当所有特征值计算出来后, 我们用下面的引理来计算特征向量. 引理 设 D ∈ R n×n 为对角矩阵, u ∈ R n , α ∈ R, 若 λ 是 D + αuu ⊺ 的特征值, 且 λ ≠ di , i = 1, 2, . . . , n, 则 (D − λI) −1u 是其对应的特征向量. (板书) http://math.ecnu.edu.cn/~jypan 23/77

算法4.1计算对称三对角矩阵的特征值和特征向量的分而治之法 1:function [Q,A]dc_eig(T) %T=Q△Q 2:if T is of1×1then 3: Q=1,A T,return 4:end if 5:form T= [0 0T2 6:[Q1,A1]dc_eig(Ti),[Q2,A2]=dc_eig(T2) 7:form D+auuT from A1,A2,Q1,Q2 8:compute the eigenvalues A and eigenvectors Q of D+auuT 0 9:compute the eigenvectors of T with= Q1 0Q2 .0 10:end 西在分而治之法中,计算特征值和计算特征向量是同时进行的
算法 4.1 计算对称三对角矩阵的特征值和特征向量的分而治之法 1: function [Q, Λ] = dc_eig(T) % T = QΛQ ⊺ 2: if T is of 1 × 1 then 3: Q = 1, Λ = T, return 4: end if 5: form T = " T1 0 0 T2 # + bmvv ⊺ 6: [Q1, Λ1] = dc_eig(T1), [Q2, Λ2] = dc_eig(T2) 7: form D + αuu ⊺ from Λ1, Λ2, Q1, Q2 8: compute the eigenvalues Λ and eigenvectors Qˆ of D + αuu ⊺ 9: compute the eigenvectors of T with Q = " Q1 0 0 Q2 # · Qˆ 10: end ✍ 在分而治之法中, 计算特征值和计算特征向量是同时进行的

秦 分而治之法的实施 下面我们详细讨论分而治之算法的几个细节问题: (1)如何减小运算量: (2)如何求解特征方程f(A)=0: (3)如何稳定地计算特征向量。 http://math.ecnu.edu.cn/~jypan 25/77
分而治之法的实施 下面我们详细讨论分而治之算法的几个细节问题: (1) 如何减小运算量; (2) 如何求解特征方程 f(λ) = 0; (3) 如何稳定地计算特征向量. http://math.ecnu.edu.cn/~jypan 25/77

秦 (1)如何减小运算量一收缩技巧(deflation) 分而治之算法的计算复杂性分析如下:用t(n)表示对n阶矩阵调用函数dc_e1g 的运算量,则 t(n)=2t(n/2)递归调用dc_eig两次 +O(n计算D+auuT的特征值和特征向量 +c.n3 计算Q. 如果计算Q时使用的是稠密矩阵乘法,则c=2;若不计O(2)项,则由递归 公式t(n)=2t(n/2)+c.n3可得t(n)≈c.4n3/3. 事实上,由于收缩(deflation)现象的存在,常数c通常比l小得多。 http://math.ecnu.edu.cn/~jypan 26/77
(1) 如何减小运算量 — 收缩技巧 (deflation) 分而治之算法的计算复杂性分析如下: 用t(n) 表示对n 阶矩阵调用函数 dc_eig 的运算量, 则 t(n) = 2 t(n/2) 递归调用 dc_eig 两次 + O(n 2 ) 计算 D + αuu ⊺ 的特征值和特征向量 + c · n 3 计算 Q. 如果计算 Q 时使用的是稠密矩阵乘法, 则 c = 2; 若不计 O(n 2 ) 项, 则由递归 公式 t(n) = 2 t(n/2) + c · n 3 可得 t(n) ≈ c · 4n 3/3. 事实上, 由于收缩 (deflation) 现象的存在, 常数 c 通常比 1 小得多. http://math.ecnu.edu.cn/~jypan 26/77