
南阳师范学院一数学与统计学院 (11)(e严y,=a0e" () 《高等数学》第二章—导数与微分练习题 (12)y=f(x)在x。可微的充要条件是y=fx)在可导 () 练习题(A) 二、填空题(将正痛答案填写在横战上) 一、判断正误题(刺断下列各愿是香正确,正确的划1,帽黄的划×) 1.若fx)=,则(x)=,f'()= (1)若函数f八x)在点x处可导,则 -2g() 2等轴双曲线y=在点山,)处的切战的斜率为一切线方程为一 Ar h (2)若函数f)在点处可导,则∫'()儿=f"() () 4若=,则装 fx,xso (3)设fx)= ,则函数f(x)在点x=0处左导数存在,右导数不存在() "ly=e-1 则心 6.若fx)=a,r+an--+an--2+…+ar+a则o(x)= [Lx>0. (4)若f(x)=sgnx=0,x=0,则f(x)在x=0处可导 () 7.若fx)=xx+1x+2)…(x+99),则f(0)= -lx<0. 8.[2sinx+4cos= 《5)fx)=-x在(←A,+∞)内只有一个不可导的点 () @-- 9.若y=入-x,x=2,Ar=0.002,L2am= () 10.(arctanx+arccotx)'= (7)若y=e产+e,则y-y=2y () 三、选择题(将正确答案的序号填可在括号内) () (1)一物体的运动方程是5=+10,则《) (9)若函数y=f(x)在点无处可导,则当Ax→0时,△y-f'气x)△x是此△r高阶 A:在1=1时的解时速度v=3 的无穷小量 () B:在1=1到1=2时的平均速度T=3 (I0)函数y=fx)在点处可微且f(x)≠0,则f+x)=f八)+f()() C:在t=I时的加速度a= D:在t=1时的加速度a=2 第1页共3页
南阳师范学院—数学与统计学院 第 1 页 共 3 页 《高等数学》第二章-——导数与微分练习题 练习题(A) 一、判断正误题(判断下列各题是否正确,正确的划√,错误的划×) (1)若函数 f ( ) x 在点 0 x 处可导,则 0 0 0 0 00 0 0 0 0 () ( ) ( ) ( ) ( ) ( ) ( ) lim lim lim xx x h f x fx fx x fx fx h fx f x → Δ→ → xx x h − +Δ − + − ′ == = − Δ ( ) (2)若函数 f ( ) x 在点 0 x 处可导,则 0 0 ( )| ( ) x x f x fx = ′ = ′ ( ) (3)设 2 1 3 , 0 ( ) , 0 x x f x x x ⎧ ≤ ⎪ = ⎨⎪⎩ > ,则函数 f ( ) x 在点 x = 0 处左导数存在,右导数不存在 ( ) (4)若 1, 0, ( ) sgn 0, 0, 1, 0. x fx x x x ⎧ > ⎪ === ⎨⎪⎩− < 则 f ( ) x 在 x = 0 处可导 ( ) (5) f () 1 xxx = − 在(, ) −∞ +∞ 内只有一个不可导的点 ( ) (6) 1 [ ln( )] x x − =− ′ ( ) (7)若 2x x y e e− = + ,则 yy y ′′ ′ − = 2 ( ) (8)曲线 sin 2 , cos , t t x e t y e t ⎧ = ⎨⎩ = 在 4 t π= 时相应点处的法线的斜率为 1 ( ) (9)若函数 y = f x( ) 在点 0 x 处可导,则当 Δx → 0时, 0 Δy − Δ fx x ′( ) 是比 Δx 高阶 的无穷小量. ( ) (10)函数 y fx = ( ) 在点 0 x 处可微且 0 f x ′() 0 ≠ ,则 0 00 f ( ) () () x x fx f x x +Δ ≈ + Δ ′ ( ) (11) (100) 100 ( ) ax ax e ae = ( ) (12)) y = f x( ) 在 0 x 可微的充要条件是 y = f x( ) 在 0 x 可导 ( ) 二、填空题(将正确答案填写在横线上) 1. 若 f ( ) x x = ,则 0 f x( ) −′ = , 0 f x( ) +′ = . 2. 等轴双曲线 1 y x = 在点(1,1) 处的切线的斜率为 ,切线方程为 . 3. sin sin lim x a x a → x a − = − 4. 若 sin ( ) x f x e = ,则 x 0 df dx = = 5. 若 1, 1, t t x e y e − ⎧ = + ⎨⎩ = − 则 dydx = 6. 若 1 2 1 2 10 ( ) nn n nn n f x ax a x a x ax a − − = + + ++ + − − " 则 ( ) ( ) n f x = 7. 若 f x xx x x ( ) ( 1)( 2) ( 99) = + + ⋅⋅⋅ + ,则 f ′(0) = 8. [ ](10) 0 2sin 4cos x x x + = = 9. 若 3 0 y x xx x = − = Δ= , 2, 0.002 , 0 2, 0.002 |x x dy = Δ= = 10. (arctan cot ) x + arc x ′ = 三、选择题(将正确答案的序号填写在括号内) (1)一物体的运动方程是 3 s t = +10 ,则( ) A:在t =1时的瞬时速度v = 3 B:在t =1到t = 2时的平均速度v = 3 C:在t =1时的加速度 a =1 D:在t =1时的加速度 a = 2

南阳师范学院一数学与统计学院 (2)下列结论错误的是() C:f但在点x处一定可导 A:当△r→0时,若△y与△r是等价无穷小量,则f"(x)存在且f()=1 g(x) B:当△x→0时,△y与△x是同阶无穷小量,则了(无)存在但(x)≠0 D:sinf(x)在点x处一定可导 C:当△x→0时△y是比△x较高阶的无穷小量,则f(,)存在且f'()=0 (7)函数f(x)=G,下列结论正确的是( D:当△r→0时△y是比△r较阶的无穷小量,则f"(x)存在 A:在(-,+0)内处处连续且可导 B:在(-力,+四)内处处连续但在x=0处不可导 (3)下列结论错误的是() A:若函数f(x)在点x=x处连续,则函数f(x)在点x=x处可导 C:在(-,+四)内处处不可导 B:若函数f(x)在点x=x,处不连续,则函数f(x)在点x=处不可导 D:在(-D,+)内处处不可微 C:若函数fx)在点x=x处可导,则函数f(x)在点x=处连续 (8)设u=(x,v=(x)可微,则下列结论正确的是() D:若函数f(x)在点x=处不可导,则函数f(x)在点x=x处也可能连续 A:d(uv)=vdu+udy B:d(uv)=dudy (4)若函数f八x)在点无,处可导,则() A:函数f(x也在点x处一一定可导B:函数√f八x)在点x处一定可导 6的= D:d(u+1)=du+1 C:函数2f产(x)+1在点x处一定可导D:函数 而在点6处一定可导 四、计算题 (5)下列结论错误的是() 1.已知y=e(sinx-cosx,求y A:函数∫(x)在点无处可导的充分必要条件是左、右导数都存在且相等 2.设y=, (x-1(x-2) (x+1(x+2) ,求y B:函数f(x)在点x。处不可导的充要条件是左、右导数都不存在 C:若左、右导数至少有一个不存在,则函数f(x)在点无处不可导 3.求曲线sin()+n(y-x)=x在点(0,)处的切线与法线方程. D:若左、右导数都存在但不相等,则函数f(x)在点,处不可导 4.参数方程 x=c0s1+1 确定函数y=f(x),求y (6)函数fx)在点处可导,函数g(x)在点x处不可导,则( (y=sint-1 5.设y=f(xsinx).其中fx)可导,求 A:f(x)士g(x)在点处一定可导 6.利用一阶微分的形式不变性求y=an1+x)在x=1处的微分山 B:fx)g(x)在点x处一定可母 第2页共3页
南阳师范学院—数学与统计学院 第 2 页 共 3 页 (2)下列结论错误的是( ) A:当 Δ →x 0时,若 Δy 与 Δx 是等价无穷小量,则 0 f ′( ) x 存在且 0 f x ′()1 = B:当 Δ →x 0时, Δy 与 Δx 是同阶无穷小量,则 0 f ′( ) x 存在但 0 f x ′() 0 ≠ C:当 Δ →x 0时 Δy 是比 Δx 较高阶的无穷小量,则 0 f ′( ) x 存在且 0 f x ′()0 = D:当 Δ →x 0时 Δy 是比 Δx 较低阶的无穷小量,则 0 f ′( ) x 存在 (3)下列结论错误的是( ) A:若函数 f ( ) x 在点 0 x = x 处连续,则函数 f ( ) x 在点 0 x = x 处可导 B:若函数 f ( ) x 在点 0 x = x 处不连续,则函数 f ( ) x 在点 0 x = x 处不可导 C:若函数 f ( ) x 在点 0 x = x 处可导,则函数 f ( ) x 在点 0 x = x 处连续 D:若函数 f ( ) x 在点 0 x = x 处不可导,则函数 f ( ) x 在点 0 x = x 处也可能连续 (4)若函数 f ( ) x 在点 0 x 处可导,则( ) A:函数 f ( ) x 也在点 0 x 处一一定可导 B:函数 f ( ) x 在点 0 x 处一定可导 C:函数 2 2 () 1 f x + 在点 0 x 处一定可导 D:函数 1f ( ) x 在点 0 x 处一定可导 (5)下列结论错误的是( ) A:函数 f ( ) x 在点 0 x 处可导的充分必要条件是左、右导数都存在且相等 B:函数 f ( ) x 在点 0 x 处不可导的充要条件是左、右导数都不存在 C:若左、右导数至少有一个不存在,则函数 f ( ) x 在点 0 x 处不可导 D:若左、右导数都存在但不相等,则函数 f ( ) x 在点 0 x 处不可导 (6)函数 f ( ) x 在点 0 x 处可导,函数 g x( ) 在点 0 x 处不可导,则( ) A: f () () x gx ± 在点 0 x 处一定可导 B: f () () x gx ⋅ 在点 0 x 处一定可导 C: ( ) ( ) f x g x 在点 0 x 处一定可导 D: sin ( ) f x 在点 0 x 处一定可导 (7)函数 3 f ( ) x x = ,下列结论正确的是( ) A:在(, ) −∞ +∞ 内处处连续且可导 B:在(, ) −∞ +∞ 内处处连续但在 x = 0 处不可导 C:在(, ) −∞ +∞ 内处处不可导 D:在(, ) −∞ +∞ 内处处不可微 (8)设u ux v vx = ( ), ( ) = 可微,则下列结论正确的是( ) A: d uv vdu udv ( ) = + B: d uv du dv ( ) = ⋅ C: ( ) u du d v dv = D: d u du ( 1) 1 += + 四、计算题 1. 已知 (sin cos ), x y = − ex x 求 x 0 y = ′ 2. 设 ( 1)( 2) ( 1)( 2) x x y x x − − = + + ,求 y′ . 3. 求曲线sin ln ( xy yx x ) + ( − =) 在点(0,1) 处的切线与法线方程. 4. 参数方程 cos 1 sin 1 x t y t ⎧ = + ⎨⎩ = − 确定函数 y fx = ( ) ,求 y′′ . 5. 设 y fx x = ( sin ) ,其中 f ( ) x 可导,求 y′ . 6. 利用一阶微分的形式不变性求 2 2 y = + tan (1 ) x 在 x =1处的微分 dy
南阳师范学院一数学与统计学院 7.利用一阶微分的形式不变性求e2y-c0s)=e-1的微分山,并求出变 五、证明题 上设清数=r芒兰革瑰本字力办 2.证明:函数f(四={e-山x50 [ax+b,x>0 在x=0处可导的充要条件是a=Lb=0. 3.证明:f(x)={ 上s之0在定义内处处可位 0x=0 第3页共3页
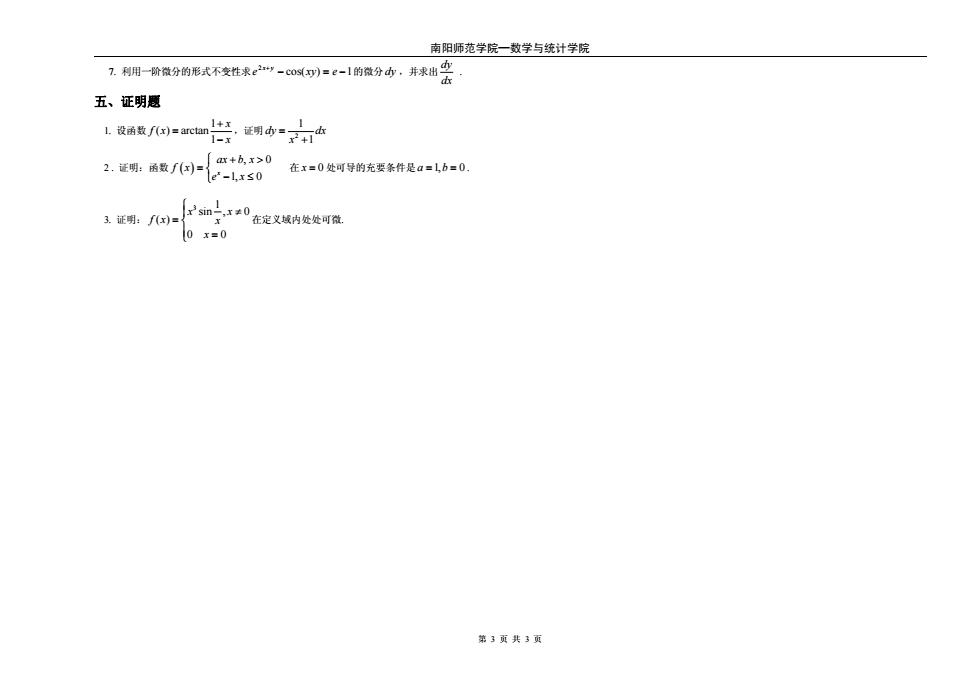
南阳师范学院—数学与统计学院 第 3 页 共 3 页 7. 利用一阶微分的形式不变性求 cos( ) 1 2 − = − + e xy e x y 的微分 dy ,并求出 dydx . 五、证明题 1. 设函数 1 ( ) arctan 1 x f x x + = − ,证明 21 1 dy dx x = + 2 . 证明:函数 ( ) , 0 1, 0 xax b x f x e x ⎧ + > = ⎨⎩ − ≤ 在 x = 0 处可导的充要条件是 a b = = 1, 0 . 3. 证明: 3 1 sin , 0 ( ) 0 0 x x f x x x ⎧⎪ ≠ = ⎨⎪⎩ = 在定义域内处处可微

南阳师范学院—一数学与统计学院 《高等数学》第二章-一导数与徽分 练习题(B) 导的、且有f)= () c(y) 一、判断正误题(州断下列各愿是香正确,正确的划1,帽漫的划X) (13)(sin2x)0=20sin2x () ①若福数国在点6处可琴,则/G)马因--A山 () (14)y=f(x)在x。不可微的充要条件是y=f(x)在无不可导 () ②)若商数)在点气处可绿,则)=四+-山 () (15)连续的曲线上每一点处都有切线 () h 、《3)着函最/)在点玉处可导,则必有Cx儿、= () 二、填空题(将正确答案填写在横线上) 4设f)= x0 ,f'(0)= () 2.若y=3x0+5x2-6x3+4,则o= (5)若f八x)=卜-,则f(x)在x=1处可号 () (6)f(x)=F在(-0,+D)内均可母 () 4若f)5csm子则 (7)若函数fm)可导,则[fnx)=f'(nx) () 在 5.若y=(l+x2)arctanx,则y= (8)若y=x2e2,则y-2y+y=0 (9)曲线+y2=2x在(,)处的法线的斜率为召 6若方程y-sin(πy)=0确定y是x的函数,则 () dx 5 7.设fx)=x(x+1)x+2)小…(x+m)(n22),则f(0)=_ m致=在点丝,且0:则回查-0 () &[e“+cos5r]lw= )当银小时,则一3安1+ () 9.若y=lnl+e)b=L,△r=0.002,dl。as-am= (12)若函数x=(y)在区间L,内单调可导,则它的反函数y=(x)在对应区间1.内总是可 10.d =sec2 4xdr. 第1页共3页
南阳师范学院——数学与统计学院 第 1 页共 3 页 《高等数学》第二章---导数与微分 练习题(B) 一、判断正误题(判断下列各题是否正确,正确的划√,错误的划×) (1)若函数 f ( ) x 在点 0 x 处可导,则 0 0 0 () ( ) ( ) limx f x fx x f x Δ → x − − Δ ′ = Δ ( ) (2)若函数 f ( ) x 在点 0 x 处可导,则 0 0 0 0 ( )( ) ( ) limh f x h fx h f x → h + − − ′ = ( ) (3)若函数 f ( ) x 在点 0 x 处可导,则必有 0 0 d( ) ( )| d x x f x f x x = ′ = ( ) (4)设 , 0 ( ) ln(1 ), 0 x x f x x x ⎧ ,则 f (0) −′ = , f (0) +′ = . 2. 若 10 7 3 yx x x = 3 564 +−+ ,则 (10) y = , (100) y = 3. cos cos lim x a x a → x a − = − 4. 若 ( ) 5arcsin 2x f x = ,则 df dx = 5. 若 2 y = + (1 ) arctan x x ,则 y′′ = 6. 若方程 2 xy y − sin( ) 0 π = 确定 y 是 x 的函数,则 dydx = 7. 设 f x xx x x n n ( ) ( 1)( 2) ( ) ( 2) = + + ⋅⋅⋅ + ≥ ,则 f ′(0) = 8. (20) 3 0 cos 5 x x e x = ⎡ ⎤ + = ⎣ ⎦ 9. 若 2 0 ln(1 ), 1, 0.002 x y ex x = + = Δ= , 0 1, 0.002 |x x dy = Δ= = 10. d = 2 sec 4xdx

南阳师范学院一数学与统计学院 北mm-。 (4)若曲线y=x2+ar+b和y=x+x在点(L,2)处相切(其中a,b是常数) 则a,b之值为( ( A:a=2,b=-1B:a=lb=-3 C:a=0,b=-2 D:a=-3,b=l 三、选择题(将正确答案的序号填写在括号内) (5)下列结论正确的是( ①若四但=1.则在x=0处() A:若左、右导数都存在,则函数f(x)在点无处可导 B:函数(x)在点处不可导的充委条件是左、右导数都不存在 A可导,且f(0)=0B:可导,且f(0)≠0 C:若函数f(x)在点x。处不可导,则函数f(x)在点x。处左、右导数只有一个不存在 C:不可导 D:以上答案都不正确 D:函数f(x)在点x。处可导的充分必要条件是左、右导数都存在且相等 (f (2)若f)可导,f0)=0,f0=0,则Fx)={x x0) (6)若函数x)、g(x)在点x处都不可导,则() 0x=0 A:(x)±g(x)在点x处一定不可号 A:在x=0处连续但不可导 B:在x=0处可号 B:fx小gx)在点处一定不可号 C:在x=0处不连续 D:在x=0处不可导 c:四在点无处一定不可 (3)下列结论错误的是《) g(x) A:函数f(x)在点x。可导是函数f工)在点无连续的充分但非必要条件 D:f土g、f)g、但在点无处可能可导,色可能不可导 g() B:函数f(x)在点x连续是函数f(x)在点x。可导的充分但辈必要条件 (7)设y=fu,=g(x)均为可微函数,则复合函数y=f(g(x》的微分d=() C:函数f(x)在点x可微是函数f(x)在点x。连续的充分但非必要条件 A:f(x)dx B:f(u)du D:函数f(x)在点x。可微是函数f(x)在点无可导的充要条件 C:f(g'(x))d D:f(g(x))g'(x)dr 第2页共3页
南阳师范学院——数学与统计学院 第 2 页共 3 页 11. 2 4 tan 1 lim 4 x x x → π π − = − 12. 1 arctan 1 x x ′ ⎛ ⎞ + ⎜ ⎟ = ⎝ ⎠ − 三、选择题(将正确答案的序号填写在括号内) (1)若 3 0 ( ) lim 1 x f x → x = ,则 f ( ) x 在 x = 0 处( ) A:可导,且 f ′(0) 0 = B:可导,且 f ′(0) 0 ≠ C:不可导 D:以上答案都不正确 (2)若 f ( ) x 可导, f f ′(0) 0, (0) 0 = = ,则 2 ( ) 0 ( ) 0 0 f x x F x x x ⎧⎪ ≠ = ⎨⎪⎩ = ( ) A:在 x = 0 处连续但不可导 B:在 x = 0 处可导 C:在 x = 0 处不连续 D:在 x = 0 处不可导 (3)下列结论错误的是( ) A:函数 f ( ) x 在点 0 x 可导是函数 f ( ) x 在点 0 x 连续的充分但非必要条件 B:函数 f ( ) x 在点 0 x 连续是函数 f ( ) x 在点 0 x 可导的充分但非必要条件 C:函数 f ( ) x 在点 0 x 可微是函数 f ( ) x 在点 0 x 连续的充分但非必要条件 D:函数 f ( ) x 在点 0 x 可微是函数 f ( ) x 在点 0 x 可导的充要条件 (4)若曲线 2 y = x ax b + + 和 3 y = x x + 在点(1, 2) 处相切(其中 a b, 是常数), 则 a b, 之值为( ) A: a b = 2, 1 = − B: a b =1, 3 = − C: a b = 0, 2 = − D: a b = − = 3, 1 (5)下列结论正确的是( ) A:若左、右导数都存在,则函数 f ( ) x 在点 0 x 处可导 B:函数 f ( ) x 在点 0 x 处不可导的充要条件是左、右导数都不存在 C:若函数 f ( ) x 在点 0 x 处不可导,则函数 f ( ) x 在点 0 x 处左、右导数只有一个不存在 D:函数 f ( ) x 在点 0 x 处可导的充分必要条件是左、右导数都存在且相等 (6)若函数 f ( ) x 、 g x( ) 在点 0 x 处都不可导,则( ) A: f () () x gx ± 在点 0 x 处一定不可导 B: f () () x gx ⋅ 在点 0 x 处一定不可导 C: ( ) ( ) f x g x 在点 0 x 处一定不可导 D: f () () x gx ± 、 f () () x gx ⋅ 、 ( ) ( ) f x g x 在点 0 x 处可能可导,也可能不可导 (7)设 y = fu u gx ( ), ( ) = 均为可微函数,则复合函数 y = f gx ( ( ))的微分 dy = ( ) A: f ′( ) x dx B: f ′( ) u du C: f ( ( )) g x dx ′ D: f ( ( )) ( ) g x g x dx ′

南阳师范学院—一数学与统计学院 四、计算题 2设函数f(x) 0x=0 L一儿 证明:(1)当p=1时,f(x)在x=0处连续不可导: 2.设f八x)=sinn.cos"x,n为常数,求y (2)当p≥2时,函数f(x)在x=0处连续且可导,且 ,求: 3.设y=+ f'(x)= 0 x=0 4.设y=(sinx),求y 5曲线F=2sm39c0s8, [In(1-x),x0 不度n心mfaw功种保且/01盘 4.证明:函数fx)在点x可微的充要条件是在点可导,且当在点f(x)可微时,其微 8.已知函数f(u)具有二阶导数,且f四=1.f)=1,函数y=x) 分一定是d山=f'(Ax 由水程-g=1所院设:=0.水经装 9利用阶微分的形式不变性求si)+y-x)=x的微分山,并求出少 10.求arcsin0.5002的近似值, 五、证明题 1.设函数fx,gx)可导,y=√f产(x)+g(x),证明 .ffx)+gxg' dx √f(x)+g() 第3页共3页
南阳师范学院——数学与统计学院 第 3 页共 3 页 四、计算题 1. 设 2 arccos , 1 x y x = − 求 x 0 y = ′ 2. 设 ( ) sin cosn f x nx x = ⋅ , n 为常数,求 y′ 3. 设 1 1 x y x x − = ⋅ + ,求 y′ . 4. 设 tan (sin ) x y x = ,求 y′ . 5. 曲线 2sin 3 cos , 3sin 3 sin , xy θ θ θ θ ⎧ = ⎨⎩ = 上对应于 3π θ = 的点处的切线与法线方程. 7. 设 2 2 ( sin ) ( cos ) x x y fe x fe x = + ,其中 f ( ) x 可导,且 f ′(1) 1 = ,求 x 0 dy dx = . 8. 已知函数 f ( ) u 具有二阶导数,且 f '(1)=1, f ′′(1) 1 = ,函数 y = y x( ) 由方程 1 1 y y xe − − = 所确定. 设 z fy = ( ),求 x 0 dz dx = , 2 2 x 0 d z dx = . 9. 利用一阶微分的形式不变性求sin( ) ln( ) xy yx x + − = 的微分 dy ,并求出 dydx . 10. 求arcsin 0.5002 的近似值. 五、证明题 1. 设函数 f ( ), ( ) x gx 可导, 2 2 y = + f x gx () () ,证明: 2 2 () () () () () () dy f x f x g x g x dx f x gx ′ ′ + = + 2 设函数 ( ) 1 sin , 0 0, 0 p x x f x x x ⎧⎪ ≠ = ⎨⎪⎩ = , 证明:(1)当 p =1时, f ( ) x 在 x = 0 处连续不可导; (2)当 p ≥ 2时,函数 f ( ) x 在 x = 0 处连续且可导,且 ( ) 1 2 1 1 sin cos , 0 0, 0 p p px x x f x x x x ⎧ − − ⎪ − ≠ ′ = ⎨⎪⎩ = . 3. 证明函数 ( ) ln(1 ), 0 0, 0 sin , 0 x x fx x x x ⎧ − 在定义域内只有一个不可导点. 4. 证明:函数 f ( ) x 在点 0 x 可微的充要条件是在点 0 x 可导,且当在点 f ( ) x 可微时,其微 分一定是 0 dy f x x = ′( )Δ

南阳师范学院一数学与统计学院 《高等数学》第二章一导数与微分 自测题(A) 二.单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码填在 题号 四 五总分 题干上的括号内.每小遥2分,共12分) 得分 1.下列结论错误的是() :若函数四低+的型不存在,则函数阳在点:5处不可导 一.判断题(判断下列各题是否正确,正确的划,错误的划×.每小题2分,共20分) h 1若5+--0,则6)=0 B:当△x→0时,若△y是比△r较低阶的无穷小量,则函数f(x)在点x=x () 处不可导 2.若函数fx)在点x处可导,则当△r→0时,fx+△x)-fx)一定是无穷小量. C:若函数f)在点x=的左右导数至少有一个不存在在,则函数fx) () 3.基本初等函数在其定义域上处处可导. () 在点x=无处不可导 x,x0 可导 2.fx)=sin在(-,+切)内不可导点有() 5.可导的偶函数的导数是奇函数 () A:1个B:2个C:3个 D:无数个 6.若函数f(x,g(x)在点x处不可导,则f(x)土g(x)在点x处也不可导.() 3.设山=x,r=r(x)可导,则下列结论正确的是() 7.(aresin x+arccosx)'=(arctanx+arccotx)'. () A:(ury=u'v+un'B:(n)'=u'.v' 8.如果单调函数x=)在某区间内可导,而且)≠0,那么它的反函数 c俏r-号 D:(u+y='+1 y=f(x)在对应的区间内也可导且(x)= 1. () ) 4.设y=f(u,=g(x)均为可微函数,则复合函数y=f八gx)的微分 9.若函数fx)在点x处可导,则当△r→0时,Ay-f'(x)△x是比△x高阶的无穷小. ▣() () A:f广(xtB:f"(adC:f八gx)D:fg(xg'(x)d 10.在区间1上,若fx)=g(x),则必有fx)=(x) () 第1页共2页
南阳师范学院—数学与统计学院 第 1 页 共 2 页 《高等数学》第二章-——导数与微分 自测题(A) 题号 一 二 三 四 五 总分 得分 一.判断题(判断下列各题是否正确,正确的划√,错误的划×。每小题 2 分,共 20 分) 1.若 0 0 0 ( ) () lim 0 x fx x fx Δ → x +Δ − = Δ , 则 0 f x ′()0 = ( ) 2.若函数 f ( ) x 在点 x 处可导,则当Δx → 0时, f ( ) () x x fx +Δ − 一定是无穷小量. ( ) 3.基本初等函数在其定义域上处处可导. ( ) 4.设 , 0 ( ) 0, 0 1, 0 x x fx x x ⎧ ,则 f ( ) x 在点 x = 0 处左、右导数都存在. ( ) 5.可导的偶函数的导数是奇函数. ( ) 6.若函数 f ( ), ( ) x gx 在点 x 处不可导,则 f () () x gx ± 在点 x 处也不可导.( ) 7. (arcsin arccos ) (arctan arc cot ) x + =+ x xx ′ ′ . ( ) 8.如果单调函数 x = ϕ( ) y 在某区间内可导,而且 ϕ′() 0 y ≠ ,那么它的反函数 y fx = ( )在对应的区间内也可导且 1 ( ) ( ) f x ϕ y ′ = ′ . ( ) 9.若函数 f ( ) x 在点 x 处可导,则当Δx → 0时,Δy − Δ fx x ′( ) 是比Δx 高阶的无穷小. ( ) 10.在区间 I 上,若 f ′ ′ () () x gx = ,则必有 f () () x gx = ( ) 二.单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码填在 题干上的括号内。每小题 2 分,共 12 分) 1.下列结论错误的是( ) A:若函数 0 0 0 ( ) () lim h f x h fx → h + − 不存在,则函数 f ( ) x 在点 0 x = x 处不可导 B:当Δx → 0时,若Δy 是比Δx 较低阶的无穷小量,则函数 f ( ) x 在点 0 x = x 处不可导 C:若函数 f ( ) x 在点 0 x = x 的左右导数至少有一个不存在在,则函数 f ( ) x 在点 0 x = x 处不可导 D:若函数 f ( ) x 在点 0 x = x 的左右导数都存在,则函数 f ( ) x 在点 0 x = x 处 可导 2. f ( ) sin x x = 在(, ) −∞ +∞ 内不可导点有( ) A: 1 个 B:2 个 C: 3 个 D:无数个 3. 设u ux v vx = ( ), ( ) = 可导,则下列结论正确的是( ) A: ( ) uv u v uv ′ = ′ ′ + B: ( ) uv u v ′ ′′ = ⋅ C: ( ) u u v v ′ ′ = ′ D: ( 1) 1 u u + =+ ′ ′ 4. 设 y fu u gx = ( ), ( ) = 均为可微函数,则复合函数 y f gx = ( ( ))的微分 dy = ( ) A: f ′( ) x dx B: f ′( ) u du C: f ( ( )) g x dx ′ D: f ( ( )) ( ) g x g x dx ′

南阳师范学院一数学与统计学院 5.下列结论错误的是() 8已知物体的运动规律是h=3+,则该物体在1=2时的加速度 A:若f(x)在点x=x处连续,则f(x)在点x=无处可微 为 B:若f(x)在点x=无处不连续,则fx)在点x=x处不可微 四.计算题(每小题6分,共30分) C:若f(x)在点x=x处可微,则f(x)在点x=无处连续 1.已知y=e(sin2x-cos2x)求y儿o D:若f(x)在点x=处不可微,则fx)在点x=x处也可能连续 ++l,求fo 2.已知函数f=acan- 6.下列结论正确的是() 3.已知y=x,求.(6分) A:函数f(x)=sgnx在定义域内处处连续且可导 B:函数f(x)=max{x,l}在定义域内处处连续且可导 4已知曲线上=cos2 ly=sin'2t ,求该曲线在1=时的切线方程。 C:函数(x)=√G在定义城内处处连续且可导 5.设y=x)是由方程e'+y-x+1=0所确定的隐函数.求微分 D:函数f(x) sm上x0在定义规内处处连续且只有一个不可导的点 五.证明题(共22分) 0,x*0 三.填空题(将正确答案填写在空格上,每小题2分,共16分) 1.证明函数f八(x)=中-在x=1处连续但不可导.(8分) 1000=1.则s- 2.证明函数f(x)= 在定义城内处处可导,并且 2.设f(x)存在,当△x→0时,若Ay与△x是等价无穷小量,则∫(x)= 0, x=0 3.lim Lanx- 。11 T=2 xsin-c0s-于x≠0.(8分】 0, x=0 4若f)=h(m),则丝。 dx 5.fx)=2m,则f(0)=_ 王设证期紧-宁0.《6分》 6.[sinxco 7.函数f(m)可导,并且f)=0.5,y=f八x2)当自变量x在x=1处取得增 △x=0.1时应的函数增量Ay的线性主部为 第2页共2页
南阳师范学院—数学与统计学院 第 2 页 共 2 页 5. 下列结论错误的是( ) A:若 f ( ) x 在点 0 x = x 处连续,则 f ( ) x 在点 0 x = x 处可微 B:若 f ( ) x 在点 0 x = x 处不连续,则 f ( ) x 在点 0 x = x 处不可微 C:若 f ( ) x 在点 0 x = x 处可微,则 f ( ) x 在点 0 x = x 处连续 D:若 f ( ) x 在点 0 x = x 处不可微,则 f ( ) x 在点 0 x = x 处也可能连续 6. 下列结论正确的是( ) A:函数 f ( ) sgn x x = 在定义域内处处连续且可导 B:函数 f ( ) max ,1 x x = { }在定义域内处处连续且可导 C:函数 f ( ) x x = 在定义域内处处连续且可导 D:函数 1 sin , 0 ( ) 0, 0 x x f x x x ⎧⎪ ≠ = ⎨⎪⎩ ≠ 在定义域内处处连续且只有一个不可导的点 三.填空题(将正确答案填写在空格上,每小题 2 分,共 16 分) 1. f f (0) 0, (0) 1 = = ′ ,则 0 ( ) limx f x → x = 2.设 0 f ′( ) x 存在,当Δ →x 0时,若Δy 与Δx 是等价无穷小量,则 0 f x ′( ) = . 3. 4 tan 1 lim 4 x x x → π π − = − . 4.若 f ( ) ln ln x x = ( ),则 df dx = . 5. sin () 2 x f x = ,则 f ′′( ) 0 = 6. (100) 101 99 0 sin cos x x x xe x x = ⎡ ⎤ + ++ + = ⎣ ⎦ 7.函数 f (u) 可导,并且 f ′(1) 0.5 = , ( ) 2 y = f x 当自变量 x 在 x =1处取得增 Δ = x 0.1时应的函数增量Δy 的线性主部为 8.已知物体的运动规律是 1 3 3 2 ht t = + ,则该物体在 t s = 2 时的加速度 为 . 四.计算题(每小题 6 分,共 30 分) 1. 已知 (sin 2 cos 2 ), x y = − ex x 求 x 0 y = ′ . 2. 已知函数 1 ( ) arctan 1 1 x f x x + = + − , 求 f ′(0) . 3. 已知 2 x y x = ,求dy .(6 分) 4. 已知曲线 3 3 cos 2 sin 2 x t y t ⎧ = ⎨⎩ = ,求该曲线在 2 t π= 时的切线方程. 5. 设 y = y x( )是由方程 1 0 y e xy x + − += 所确定的隐函数.求微分dy . 五.证明题(共 22 分) 1.证明函数 f () 1 x x = − 在 x =1处连续但不可导.(8 分) 2.证明函数 2 1 sin , 0 ( ) 0, 0 x x f x x x ⎧⎪ ≠ = ⎨⎪⎩ = 在定义域内处处可导,并且 1 1 2 sin cos , 0 ( ) 0, 0 x x f x x x x ⎧⎪ − ≠ ′ = ⎨⎪⎩ = . (8 分) 3. 设 2 2 x y − =1, 证明 2 2 3 1 ( 0) d y y dx y = − ≠ . (6 分)
南阳师范学院一数学与统计学院 《高等数学》第二章— 导数与微分 () 自测题(B) 10.在区间1上,若fx)=gx),则必有fx)=g(x)+1 题号 五 总分 二.单项选择题(在每小愿的备选答案中选出一个正确答案,并将正确答案的代码填在通于上 得分 的括号内。每小题2分,共2分) 1.下列结论错误的是() 一判断题(判断下列各题是否正确,正确的划,错误的划×,每小题2分,共20分》 :若函数四--山不存在.则函数/在点:气处不可号 1若商数八四在点气处可,则必有经织型 .() dx B:函数fx)在点x=x处可微的充要条件是函数f(x)在点x=x,处可导 2若函数f(x)在点x处可微,则当△r→0时,fr+△r)-fx)一定是无穷小量. C:函数fx)在点x=无处连续是函数f)在点x=x处可导的充分不必要条件 () D:函数f(x)在点x=无处可微是函数f(x)在点x=x,处连续的充分不必要条件 3.初等函数在其定义区间上处处可导 () 2.f(x)=senx.tanx在定义域内不可导点有( [sinx,x0 3.则下列结论正确的是() 五若=以=a可绿,则=,且白=号 () A:可导的偶函数的导数是偶函数 B:可导的奇函数的导数是奇函数 6.若函数f,g)在点x处不可导,则因在点x处也不可导 () g(x) C:可导的偶函数的导数是奇函数 2 7.(arctan x-(arcsin xarccosx)= () D:可导的周期函数的导数不是周期函数 4.设y=f(m,=g(x)均为可微函数,则复合函数y=f八g(x》的微分 8.如果单调函数x=(y)在某区间内可导,那么它的反函数y=f(x)在对应的区间 办=() 内也可导且f闭 1 () A:f(x)dx B:f(u)du C:f(g'(x))dx D:f(g(x))g'(x)d 9.若函数f在点x处可导,则当Ar→0时,4y-∫x)Ar是与△r等价的无穷小.5.若/)=+2x-6+4红+1,则() () A:当k=99时,(x)=99xB:当k=100时,f(x)=0 第1页共2页
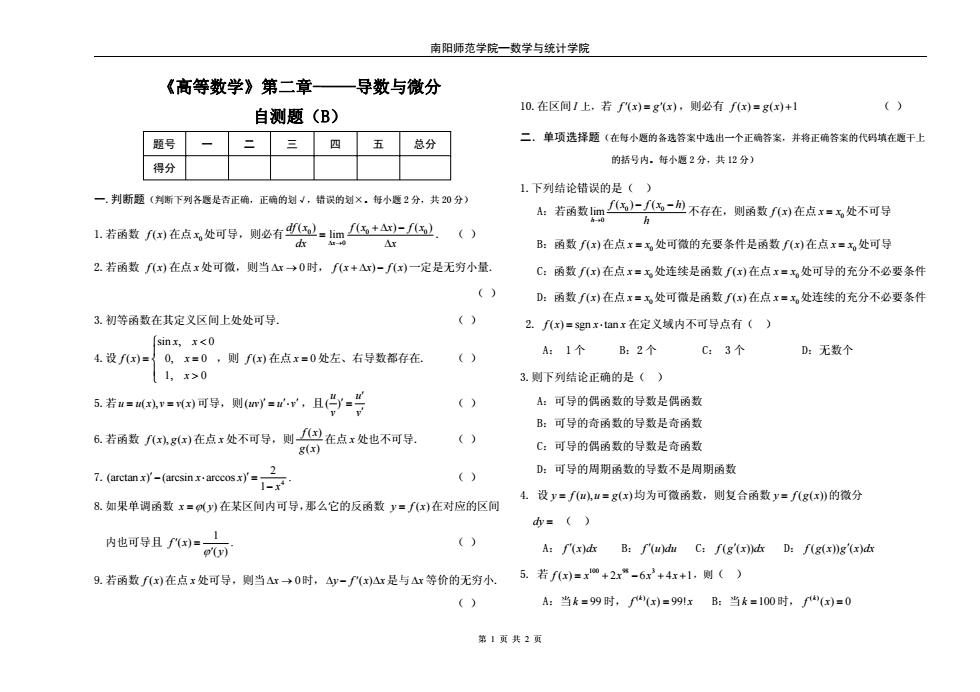
南阳师范学院—数学与统计学院 第 1 页 共 2 页 《高等数学》第二章-——导数与微分 自测题(B) 题号 一 二 三 四 五 总分 得分 一.判断题(判断下列各题是否正确,正确的划√,错误的划×。每小题 2 分,共 20 分) 1.若函数 f ( ) x 在点 0 x 处可导,则必有 000 0 () ( ) () limx df x f x x f x dx x Δ → +Δ − = Δ . () 2.若函数 f ( ) x 在点 x 处可微,则当Δx → 0时, f ( ) () x x fx +Δ − 一定是无穷小量. ( ) 3.初等函数在其定义区间上处处可导. ( ) 4.设 sin , 0 ( ) 0, 0 1, 0 x x fx x x ⎧ ,则 f ( ) x 在点 x = 0 处左、右导数都存在. ( ) 5.若u ux v vx = = ( ), ( ) 可导,则( ) uv u v ′ = ′ ′ ⋅ ,且( ) u u v v ′ ′ = ′ ( ) 6.若函数 f ( ), ( ) x gx 在点 x 处不可导,则 ( ) ( ) f x g x 在点 x 处也不可导. ( ) 7. 4 2 (arctan ) (arcsin arccos ) 1 x xx x ′ ′ −⋅ = − . ( ) 8.如果单调函数 x = ϕ( ) y 在某区间内可导,那么它的反函数 y = f x( )在对应的区间 内也可导且 1 ( ) ( ) f x ϕ y ′ = ′ . ( ) 9.若函数 f ( ) x 在点 x 处可导,则当Δx → 0时,Δy − Δ fx x ′( ) 是与Δx 等价的无穷小. ( ) 10.在区间 I 上,若 f ′() () x gx = ′ ,则必有 f x gx () () 1 = + ( ) 二.单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码填在题干上 的括号内。每小题 2 分,共 12 分) 1.下列结论错误的是( ) A:若函数 0 0 0 () ( ) lim h f x fx h → h − − 不存在,则函数 f ( ) x 在点 0 x = x 处不可导 B:函数 f ( ) x 在点 0 x = x 处可微的充要条件是函数 f ( ) x 在点 0 x = x 处可导 C:函数 f ( ) x 在点 0 x = x 处连续是函数 f ( ) x 在点 0 x = x 处可导的充分不必要条件 D:函数 f ( ) x 在点 0 x = x 处可微是函数 f ( ) x 在点 0 x = x 处连续的充分不必要条件 2. f ( ) sgn tan x xx = ⋅ 在定义域内不可导点有( ) A: 1 个 B:2 个 C: 3 个 D:无数个 3.则下列结论正确的是( ) A:可导的偶函数的导数是偶函数 B:可导的奇函数的导数是奇函数 C:可导的偶函数的导数是奇函数 D:可导的周期函数的导数不是周期函数 4. 设 y fu u gx = ( ), ( ) = 均为可微函数,则复合函数 y f gx = ( ( ))的微分 dy = ( ) A: f ′( ) x dx B: f ′( ) u du C: f ( ( )) g x dx ′ D: f ( ( )) ( ) g x g x dx ′ 5. 若 100 98 3 f () 2 6 4 1 xx x x x = + − ++ ,则( ) A:当k = 99 时, ( ) ( ) 99! k f x x = B:当k =100 时, ( ) () 0 k f x =

南阳师范学院一数学与统计学院 C:当k>100时,()=1D:以上答案都不正确 2.已知函数y=(1+x)arctanx,求f(o.(7分) 6.下列结论正确的是() 3.已知y=(sin),求.(7分) A:函数f(x)=im在定义域内处处连续且可导 4已知=o2,求 B:函数fx)=max{x,l}在定义域内处处连续且可导 ly=sin'2t .(8分) 5.设函数y=f(x)由方程方程y-xe'+1=0所确定,求曲线y=f(x)在点(0,-l)处 xsin C:函数f(x)三 0在定义域内只有一个不可导的点 0, x=0 的法线方程.(8分) D:函数f(x)=x在L,2]处处连续且可导 五.证明题(共20分) 三.填空题(将正确答案填写在空格上,每小题2分,共12分) 1.证明函数f(x)=xsinx在r=0连续且可导(6分) etin:-1,x0 2.若)=0f)=1,则im国 esm:cosxx0 (2ko 3.设函数f八x)在x=1的某邻域内可导,且f()=e9,f)=0,证明: fa(=(n-1)月 (6分) 5.函数f(w可导,y=fx2nx)当自变量x在x=1处取得增量△r=0.1时,相应的 函数增量△y的线性主部为0.1,则0)= 6.若曲线y=am产+b与y=2lnx在点(l,0)处相切,则a=一b=一 四.计算题(共6分) 1.已知y=n[cos1-r小,求y.(6分) 第2页共2页
南阳师范学院—数学与统计学院 第 2 页 共 2 页 C:当k >100 时, ( ) (1) 1 k f = D:以上答案都不正确 6. 下列结论正确的是( ) A:函数 f ( ) sin x x = 在定义域内处处连续且可导 B:函数 f ( ) max ,1 x x = { }在定义域内处处连续且可导 C:函数 ( ) 1 sin , 0 0, 0 x x f x x x ⎧⎪ ≠ = ⎨⎪⎩ = 在定义域内只有一个不可导的点. D:函数 f () [] x x = 在[1, 2]处处连续且可导 三.填空题(将正确答案填写在空格上,每小题 2 分,共 12 分) 1. 设 0 f ′( ) x 存在,当Δ →x 0时,若Δy 与Δx 是高阶无穷小量,则 0 f x ′( ) = . 2. 若 0 0 fx f x ( ) 0, ( ) 1 = = ′ ,则 0 10 0 ( ) lim x x f x → x x = − . 3. ( ) 1 2 x x − =− ′ = . 4. (100) 2 1 x 4 x 0 ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ − = . 5.函数 f (u) 可导, 2 y = fx x ( ln ) 当自变量 x 在 x =1处取得增量Δx = 0.1时,相应的 函数增量Δy 的线性主部为0.1,则 f ′(0) = . 6.若曲线 2 y ax b = + 与 y x = 2ln 在点(1, 0) 处相切,则a = ,b = . 四.计算题(共 36 分) 1. 已知 ( ) 2 y x = − ln cos 1 , ⎡ ⎤ ⎣ ⎦ 求 y′.(6 分) 2. 已知函数 ( ) 2 y = +1 arctan x x , 求 f ′′(0) .(7 分) 3. 已知 ( )tan 2 sin x y x = ,求dy .(7 分) 4. 已知 3 3 cos 2 sin 2 x t y t ⎧ = ⎨⎩ = ,求 2 2 d y dx . (8 分) 5. 设函数 y = f x( ) 由方程方程 1 0 y y xe − + = 所确定,求曲线 y = f x( ) 在点(0, 1) − 处 的法线方程. (8 分) 五.证明题(共 20 分) 1.证明函数 3 f ( ) sin x xx = 在 x = 0 连续且可导(6 分) 2.证明函数 sin 1, 0 ( ) 0, 0 ln(1 ), 0 x e x f x x x x ⎧ − 在定义域内处处可导,并且 sin cos 0 1, 0 ( ) 1 , 0 1 x e xx x f x x x ⎧ ⎪⎩ + . (8 分) 3. 设函数 f () 1 x x 在 = 的某邻域内可导,且 ( ) ( ) ,10 ( ) f x fx e f ′ = = ,证明: ( ) ( ) 1 ( 1)! n f n = − (6 分)