
南阳师范学院一数学与统计学院 《高等数学》第五章一定积分 5)知果广=1则长=号 () 练习题(A) (16)若函数fx)在区同(~,+切)上连续,当f()为奇函数时,函数心f山 一、判断正误题:(判断下列各愿是否正确,正确的划,增视的划×) )=(合子…别 为偶函数.当f)为偶函数时,f边为奇函数 () () 二、选择愿:(将正确答来的序号填写在括号内) (2)=f(uydu. () (1)在闭区间[-L,]上不可积的函数是() (4)若函数f(x)在区间(-0,+m)上连续,a,b,c为任意三个常数.则 xsim,x0, A:f(x)= B:f(x)= fx=fxh+f. () 0,x=0. 0,x=0 (5)fusfin(+s. () C:f(x)=sgnx D:) (6)sin'drs "sin。 () (2)若函数f(x)在闭区间引a,b]上可导,则下列等式不一定成立的是() (7)Isfe'dsse. () B:d(f(ds)=0 国sr=as A:ff达=可fd () (9)当x→0时广sin产山与x2是等价无穷小. () c ea-Caa叫reh=o-a (10)不能直接使用牛顿菜布尼数公式求sg即止 () (3)若函数f(x)和g(x)在闭区间[a,b]上都连续,则下列等式不一定成立的是() (11)若[fth=xnx,则fx)=x+2rnx () A:f(x)g(xyd=广f达grh. )由厂由+o=0角院用=,则空-子( B:∫kfx达=fx)d(居为常数) c:f=-f(ais (13)参数方程 11在1=2时相应点处的法线的斜岸为-2.() D:[fx±gh=∫fx达±grt y=cost. (4)若函数f(x)在闭区间-a,a可上都连续,则下列等式成立的是() (14)若曲线y=r与x=1及y=0所围成的图形的面积为1,则a=2.() A:f(xr=0. B.(=f()+(x. 第1页共3页
南阳师范学院—数学与统计学院 第 1 页 共 3 页 《高等数学》第五章-——定积分 练习题(A) 一、判断正误题:(判断下列各题是否正确,正确的划√,错误的划×) (1) 1 22 2 0 1 2 limn n xdx →+∞ nn n ⎛ ⎞ ⎜ ⎟ + +⋅⋅⋅+ = ⎝ ⎠ ∫ . ( ) (2) () () b b a a f x dx f u du = ∫ ∫ . ( ) (4)若函数 f ( ) x 在区间(,) −∞ +∞ 上连续, abc , , 为任意三个常数,则 () () () b cb a ac f x dx f x dx f x dx = + ∫∫∫ . ( ) (5) 1 1 0 0 xdx x dx ≤ + ln(1 ) ∫ ∫ . ( ) (6) 2 2 sin sin b b a a x dx x dx ≤ ∫ ∫ . ( ) (7) 1 2 0 1 x ≤ ≤ e dx e ∫ . ( ) (8) ( 2 ) 2 2 cos cos x x d t dt x dx = ∫ . ( ) (9)当 x → 0 时 2 0 sin x t dt ∫ 与 2 x 是等价无穷小. ( ) (10)不能直接使用牛顿-莱布尼兹公式求 1 1sgn xdx ∫− . ( ) (11)若 2 0 ( ) ln x f t dt x x = ∫ ,则 f ( ) 2 ln x x xx = + . ( ) (12)由 2 1 1 cos 0 y x t e dt t dt + = ∫ ∫ .确定隐函数 y = f x( ) ,则 2 cosy dy x dx e = .( ) (13)参数方程 1 sin , cos . t u x u y t ⎧ ⎪ = ⎨ ⎪ ⎩ = ∫ 在t = 2时相应点处的法线的斜率为 − 2 . ( ) (14)若曲线 y = ax 与 x =1及 y = 0所围成的图形的面积为 1,则 a = 2 .( ) (15)如果 2 ln 1, e e k xdx x = ∫ 则 2 3 k = ( ) (16)若函数 f ( ) x 在区间(,) −∞ +∞ 上连续,当 f ( ) x 为奇函数时,函数 0 ( ) x f t dt ∫ 为偶函数。当 f ( ) x 为偶函数时, 0 ( ) x f t dt ∫ 为奇函数. ( ) 二、选择题:(将正确答案的序号填写在括号内) (1)在闭区间[ 1,1] − 上不可积的函数是( ) A: 1 sin , 0, ( ) 0, 0. x x f x x x ⎧ ⎪ ≠ = ⎨ ⎪ ⎩ = B: 2 2 1 sin , 0, ( ) 0, 0. x x f x x x ⎧ ⎪ ≠ = ⎨ ⎪ ⎩ = C: f ( ) sgn x x = D: 1 ( ) ( 1) f x x x = − (2)若函数 f ( ) x 在闭区间[,] a b 上可导,则下列等式不一定成立的是( ) A: () () b b a a f x dx f x dx = ∫ ∫ B: ( ) () 0 b a d f x dx = ∫ C: ( ) () () b a d d f x dx f x dx dx dx ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ ∫ ∫ D: () () () b a f ′ x dx f b f a = − ∫ (3)若函数 f ( ) x 和 g x( ) 在闭区间[,] a b 上都连续.,则下列等式不一定成立的是( ) A: ()() () () b bb a aa f x g x dx f x dx g x dx = ∫ ∫∫ . B: () () b b a a k f x dx k f x dx = ∫ ∫ ( k 为常数). C: () ( ) b a a b f t dt f x dx = − ∫ ∫ D: [ ] () () () () b bb a aa f x g x dx f x dx g x dx ±= ± ∫ ∫∫ (4)若函数 f ( ) x 在闭区间[ ,] −a a 上都连续.,则下列等式成立的是( ) A: () 0 a a f x dx − = ∫ . B: [ ] 0 () () ( ) a a a f x dx f x f x dx − = +− ∫ ∫

南阳师范学院一数学与统计学院 C: (=2f D:f(s=f()( B:函数(x)在(-,+o)上无极值点 (5)若函数fx)在闭区间[a,b]上都连续,则下列说法不正确的是() C:曲线y=x)在(-,0)上是凹的,在(0,)上是凸的 A: fh是x的函数 B心f产h是x的函数 D:函数(x)在(-,+D)上无驻点 c:广f0t是x的函数 D:心fh是x的函数 (9)下列各式中错误的是() 心ft是1的函数 A本=0 B.(d=d() E: F:心fx达是需数 (6)若函数fx)在闭区同[ab]上连线,x∈[a,b小.w(x)=fuh,则下 C:tan x =-In2 D:[2 In2dx=1 列说法不一定正确的是() (10)摆线F=-c0s1 A:)在闭区间a,上连续且mx)=广f0d {=1-sin一携(0s1≤2a)的领长是() B:(x)在闭区间[a,b]上可微且d(x)=fx) A:V+-sin旷dh B:+(cost)dr C:若函数风x)在闭区间a,上可导,则例x》在闭区间[a,] c:f店i+cosid D:-cosi di (1I)设r(在a,]上连续.则由曲线r=(0)及射线0=a、日=B(a0,直线x=a,x=b(acosh A:f2x+l在=F2b+)-F2a+ ⑧)设函数0=。a:则下列说法不正确的是() B:e'f(e")dx=F(b)-F(a) c.∫广see2 f(tanx)本=F(tanb)-Fa A:函数(x)在(-9,+0)上单调递增 第2页共3页
南阳师范学院—数学与统计学院 第 2 页 共 3 页 C: 0 () 2 () a a a f x dx f x dx − = ∫ ∫ D: [ ] 0 () () ( ) a a a f x dx f x f x dx − = −− ∫ ∫ (5)若函数 f ( ) x 在闭区间[,] a b 上都连续.,则下列说法不正确的是( ) A: ( ) x a f t dt ∫ 是 x 的函数 B: 2 ( ) bx f t dt ∫ 是 x 的函数 C: 2 ( ) x x f t dt ∫ 是 x 的函数 D: ( ) ba f xt dt ∫ 是 x 的函数 E: ( ) b a f xt dt ∫ 是 t 的函数 F: ( ) ba f x dx ∫ 是常数 (6)若函数 f ( ) x 在闭区间[,] a b 上连续., x∈[ , ]. a b ( ) () x a Φ = x f t dt ∫ ,则下 列说法不一定正确的是( ) A:Φ( ) x 在闭区间[,] a b 上连续且 lim ( ) ( ) b x b a x f t dt → − Φ = ∫ B:Φ( ) x 在闭区间[,] a b 上可微且 d x f x dx Φ() () = C:若函数ϕ( ) x 在闭区间[,] a b 上可导,则Φ( ( )) ϕ x 在闭区间[,] a b 上也可导且( ) ( ( )) ( ( )) ϕ ϕ x f x Φ =′ D:若函数ϕ( ) x 在闭区间[,] a b 上可导,则Φ( ( )) ϕ x 在闭区间[,] a b 上也可导且( ) ( ( )) ( ( )) ( ) ϕ ϕϕ x fx x ′ Φ = ′ (7)根据定积分的几何意义,下列各式中正确的是( ) A: 0 2 1 4 − = x dx π ∫ B: 20 sin 0 xdx π = ∫ C: 0 sin 0 xdx π = ∫ D: 20 2 cos cos xdx xdx π π π > ∫ ∫ (8)设函数 2 2 0 ( ) t x Φ = x e dt ∫ ,则下列说法不正确的是( ) A:函数Φ( ) x 在(,) −∞ +∞ 上单调递增 B:函数Φ( ) x 在(,) −∞ +∞ 上无极值点 C:曲线 y = Φ( ) x 在( ,0) −∞ 上是凹的,在(0, ) ∞ 上是凸的 D:函数Φ( ) x 在(,) −∞ +∞ 上无驻点 (9)下列各式中错误的是( ) A: 1 1 l dx 0 x − = ∫ B: 22 2 2 ( ) () () b b a a xf x dx f t d t = ∫ ∫ C: 3 tan ln 2 xdx π π = − ∫ D: 10 2 ln 2 1 x dx = ∫ (10)摆线 1 cos sin x t y t t ⎧ = − ⎨⎩ = − 一拱(0 2 ≤ ≤t π ) 的弧长是( ) A: 2 2 0 1 ( sin ) t t dt π + − ∫ B: 2 2 0 1 (cos )t dt π + ∫ C: 2 0 1 cost dt π + ∫ D: 20 2 1 cost dt π − ∫ (11)设 r( ) θ 在[, ] α β 上连续. 则由曲线 r = r(θ ) 及射线θ =α 、θ = β (α 、直线 x = ax b , = ( ) a b < 及 x 轴所围成的曲边梯形绕 x 轴旋 转一周而成的旋转体的体积为( ) A: 2 [ ( )] b a f x dx ∫ B: ( ) ba π f x dx ∫ C: ( ) ba f x dx ∫ D: 2 [ ( )] ba π f x dx ∫ (13)如果 F x( )是 f ( ) x 的原函数,则下列式子成立的是( ) A: (2 1) (2 1) (2 1) b a f x dx F b F a + = +− + ∫ B: ( ) () () b x x a e f e dx F b F a = − ∫ C: 2 sec (tan ) (tan ) ( ) b a xf x dx F b F a = − ∫

南阳师范学院一数学与统计学院 :/a)在=Fthj-Fa (9)设n2x是fx)在L,2]上的一个原函数,则寸x本= (4)下列积分中不是反常积分的是() 四、计算题 A杰 B 1.求下列定积分 e )晒 o (3)xlnxds (15)下列反常积分收敏的是() A广psn B:(p w月原a ( )导 c 以 2.求下列极限 frd 三、填空题(将正确答案的序号填写在捂号内) (1)f)=x2在0,上的平均值为 (1)-sinryd @=5层…月 (2)(sin2x+cos2 3.求曲线y=x之与直线y=2x用成的图形的面积 ao 4求函数广四女在区间化x+)的极大值点 五、证明题 1.设fx)在-1,上连续,f)<0.证明方程x-f女=0在(-1,山有且仅有一个 根. of 2.设f(x)在(-,)上有连续的导数,证明 o22 -ie+-0-a 3.若函数f)在闭区间[a,上连线,x∈a,.证明函数(x)=广fh可号 (8)设fx)在[0,上连续,fxh=1,则[f0-x达= 且wx)=f(x) 第3页共3页
南阳师范学院—数学与统计学院 第 3 页 共 3 页 D: 1 (ln ) (ln ) (ln ) b a f x dx F b F a x = − ∫ (14)下列积分中不是反常积分的是( ) A: 1 1 dx x ∞ ∫ B: 2 1 1 dx x ∞−∞ + ∫ C: 1 0 2 1 1 dx − x ∫ D: 2 1ln e dx x x ∫ (15)下列反常积分收敛的是( ) A: 1 l ( 1) p dx p x +∞ ≤ ∫ B: 1 l ( 1) p dx p x +∞ > ∫ C: 1 2 1 l dx x ∫− D: 11 l dx x ∫− 三、填空题(将正确答案的序号填写在括号内) (1) 2 f ( ) x x = 在[0,1] 上的平均值为 (2) ( ) 20 sin 2 cos 2 x x dx π + = ∫ (3) 1 2 0 1 1 4 dx x = + ∫ (4) 2 2 1 2 1 x dx x x + = + ∫ (5) 0 cos 1 sin x dx x π = − ∫ (6) 2 4 0 sin xdx x π = ∫ (7) 1 2 0 1 2 2 dx x x = − + ∫ (8)设 f ( ) x 在[0,1] 上连续, 1 0 f () 1 x dx = ∫ ,则 10 f (1 ) − x dx = ∫ (9)设 2 ln x 是 f ( ) x 在[1, 2] 上的一个原函数,则 21 xf x dx ′( ) = ∫ 四、计算题 1. 求下列定积分 (1) 1 1 x dx ∫− (2) 40 l 1+ dx x ∫ (3) 1 ln e x xdx ∫ (4) 2 2 6 sin 1 cos x dx x π π − ∫ (5) 2 0 1 1 dx x ∞ + ∫ (6) 1 2 0 1 dx x ∫ 2. 求下列极限 (1) 4 0 0 0 lim ( sin ) x x x t dt t t t dt → + − ∫ ∫ (2) 33 3 1 2 limn n →+∞ nn n ⎛ ⎞ ⎜ ⎟ + +⋅⋅⋅+ ⎜ ⎟ ⎝ ⎠ 3. 求曲线 2 y = x 与直线 y x = 2 围成的图形的面积 4. 求函数 1 x sin tdt t ∫ 在区间(1, 1) π + 的极大值点. 五、证明题 1.设 f ( ) x 在[ 1,1] − 上连续, f x( ) 0. < 证明方程 1 () 0 x x f x dx − − = ∫ 在 ( 1,1) − 有且仅有一个 根. 2. 设 f ( ) x 在(,) −∞ +∞ 上有连续的导数,证明: [ ] 2 0 1 lim ( ) ( ) x x x f t x f t x dt x + + → − +− − ∫ 3. 若函数 f ( ) x 在闭区间[,] a b 上连续., x∈[ , ]. a b 证明函数 ( ) () x a Φ = x f t dt ∫ 可导 且Φ′() () x = f x

南阳师范学院一数学与统计学院 《高等数学》第五章—定积分 a=2. () 练习题(B) (14)知果ed=e,则x=l () 一、判断正误题:(判断下列各题是否正确,正确的划,帽提的划X) (15)若函数fx)在区间(-,+o)上连续,当fx)为奇函数时,函数心fd () 为偶函数,当fx)为偶函数时,广fh为奇函数 () (2)=f(uydu. () 二、选择愿:(将正确答案的序号填写在括号内) (3)若函数f(x)在区间(-,+o)上连续,a,b,c为任意三个常数,则 (1)在闭区间[-1,上不可积的函数是() fx=fx+fx女。 () A:f(x)= xsin-0 B:f(x)= (④Indss(nxyds. () 0,x=0. 0,x=0. (5)"cosdr scos () C:f(x)=sgnx D:f()=(-1) o≤直+smhs2z () (2)下列等式正确的是() A:「f'x)=fx) (oxom B.r)-c () c.4r)= D:'f(xyds=f(b)-f(a) (8)当x→0时,l+h与是等价无穷小 () (3)若函数f八x)和g(x)在闭区间[a,b]上都连续,则下列等式不一定成立的是() (9)不能直接使用牛顿菜布尼兹公式求广sin山 A:广fxgr达=广fa[grt (10)若fh=rx2sinx,则fx)=2 xsinx+x2cosx () B:∫fx达=∫fd(k为常数). 设=y-则要-号 () c:f心ft=-fx达 (2)了'山+八snd=0在后0小时相应点处的法线的斜率为-1.() D:[fa±gh=fx±广gxt (4)若函数f(x)在闭区间[-a,d上都连续,则下列等式成立的是() (13)若曲线y=aπ2与x=1及y=0所围成的图形的面积为1,则 A:f(=0. B:Cf=心f+f-x本. 第1页共3页
南阳师范学院—数学与统计学院 第 1 页 共 3 页 《高等数学》第五章-——定积分 练习题(B) 一、判断正误题:(判断下列各题是否正确,正确的划√,错误的划×) (1) 1 0 11 1 1 lim n 12 1 dx →+∞ n n nn x ⎛ ⎞ ⎜ ⎟ + +⋅⋅⋅+ = ⎝ ⎠ ++ + + ∫ . ( ) (2) () () b b a a f x dx f u du = ∫ ∫ . ( ) (3)若函数 f ( ) x 在区间(,) −∞ +∞ 上连续, abc , , 为任意三个常数,则 () () () b cb a ac f x dx f x dx f x dx = + ∫∫∫ . ( ) (4) 2 2 2 1 1 ln (ln ) xdx x dx ≤ ∫ ∫ . ( ) (5) 2 2 cos cos b b a a x dx x dx ≤ ∫ ∫ . ( ) (6) ( ) 5 2 4 4 1 sin 2 x dx π π ≤+ ≤ π π ∫ . ( ) (7) ( ( ) ) 22 2 0 cos 2 cos d x x t dt x x dx = ∫ . ( ) (8)当 x → 0 时, 0 ln(1 ) x + t dt ∫ 与 2 x 是等价无穷小. ( ) (9)不能直接使用牛顿-莱布尼兹公式求 2 0 sin x dx π ∫ . ( ) (10)若 2 0 ( ) sin x f t dt x x = ∫ ,则 2 f ( ) 2 sin cos x x xx x = + . ( ) (11)设 2 0 0 , , t t u x = = e du y u du ∫ ∫ 则 2 t dy e dx t = . ( ) (12) 2 1 sin 0 y x t e dt tdt + = ∫ ∫ 在 ,0 2 ⎛ ⎞ π⎜ ⎟ ⎝ ⎠时相应点处的法线的斜率为 −1. ( ) (13)若曲线 2 y = ax 与 x =1及 y = 0所围成的图形的面积为 1,则 a = 2 . ( ) (14)如果 0 , x t e dt e = ∫ 则 x =1 ( ) (15)若函数 f ( ) x 在区间(,) −∞ +∞ 上连续,当 f ( ) x 为奇函数时,函数 0 ( ) x f t dt ∫ 为偶函数,当 f ( ) x 为偶函数时, 0 ( ) x f t dt ∫ 为奇函数. ( ) 二、选择题:(将正确答案的序号填写在括号内) (1)在闭区间[ 1,1] − 上不可积的函数是( ) A: 1 sin , 0, ( ) 0, 0. x x f x x x ⎧⎪ ≠ = ⎨⎪⎩ = B: 2 2 1 sin , 0, ( ) 0, 0. x x f x x x ⎧⎪ ≠ = ⎨⎪⎩ = C: f ( ) sgn x x = D: 1 ( ) ( 1) f x x x = − (2)下列等式正确的是( ) A: f ′() () x dx f x = ∫ B: ( ) () () d f x dx f x C dx = + ∫ C: ( ) () () ba d f x dx f x dx = ∫ D: () () () ba f ′ x dx f b f a = − ∫ (3)若函数 f ( ) x 和 g x( ) 在闭区间[,] a b 上都连续.,则下列等式不一定成立的是( ) A: ()() () () b bb a aa f x g x dx f x dx g x dx = ∫ ∫∫ . B: () () b b a a k f x dx k f x dx = ∫ ∫ ( k 为常数). C: () ( ) b a a b f t dt f x dx = − ∫ ∫ D: [ ] () () () () b bb a aa f x g x dx f x dx g x dx ±= ± ∫ ∫∫ (4)若函数 f ( ) x 在闭区间[ ,] −a a 上都连续,则下列等式成立的是( ) A: () 0 a a f x dx − = ∫ . B: [ ] 0 () () ( ) a a a f x dx f x f x dx − = +− ∫ ∫

南阳师范学院一数学与统计学院 c.=2f( D:(s=ff()-f() 9)设f=-1sr0)上相应于从变到的-一段孤与极轴所围成的图形的面积() B: 2c以m2x C:F(i=f() D:F(=f()-f(a) )清线7=(宁子写引黄新国成的图线:装美联一周商成的度装体销体银 (6)若函数f)在闭区同[a,上连线…x∈[a,o(x)=ft,则下 为() 列说法不一定正确的是() A:(x)在闭区同a,上连续且m中x)=广f边 A B: (12)下列反常积分收敛的是() B:x)在闭区间[a,]上可微且dx)=fxdk C:若函数网x)在闭区间[a,]上可导,则④例x》在驱间[a,] A:"sind 上也可导且(④((x》'=f八x) c D:e'ds D:若函数(x)在闭区间[a,b]上可导,则④(x)》在周区间[a,b] 三、填空题(将正确答案的序号填写在塘号内) 上也可导且(((x)=f八x)p'(x) (1)f(x)=e在0,】上的平均值为 (7)根据定积分的几何意义,下列各式中正确的是() (2)(sin3x+cos3= A:-天h=牙 B值sh=cosh 2 oi c∫sind=0 w… ③商最=导h在-肚有() 6 A:极大值 B:极小值 C驻点D:拐点 第2页共3页
南阳师范学院—数学与统计学院 第 2 页 共 3 页 C: 0 () 2 () a a a f x dx f x dx − = ∫ ∫ D: [ ] 0 () () ( ) a a a f x dx f x f x dx − = −− ∫ ∫ (5)设函数 f ( ) x 是连续函数且 f () () x dx F x C = + ∫ ,则必有( ) A: () ( ) x a f t dt F x = ∫ B: () ( ) xa F t dt F x ′ ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ ∫ C: () ( ) x a F t dt f x ′ = ∫ D: () ( ) ( ) xa F t dt f x f a ′ ⎡ ⎤ ′ = − ⎢ ⎥ ⎣ ⎦ ∫ (6)若函数 f ( ) x 在闭区间[,] a b 上连续., x∈[ , ]. a b ( ) () x a Φ = x f t dt ∫ ,则下 列说法不一定正确的是( ) A:Φ( ) x 在闭区间[,] a b 上连续且 lim ( ) ( ) b x b a x f t dt → − Φ = ∫ B:Φ( ) x 在闭区间[,] a b 上可微且 d x f x dx Φ() () = C:若函数ϕ( ) x 在闭区间[,] a b 上可导,则Φ( ( )) ϕ x 在闭区间[,] a b 上也可导且( ) ( ( )) ( ( )) ϕ ϕ x f x Φ =′ D:若函数ϕ( ) x 在闭区间[,] a b 上可导,则Φ( ( )) ϕ x 在闭区间[,] a b 上也可导且( ) ( ( )) ( ( )) ( ) ϕ ϕϕ x fx x ′ Φ = ′ (7)根据定积分的几何意义,下列各式中正确的是( ) A: 0 2 1 4 − = x dx π ∫ B: 3 2 2 2 2 cos cos xdx xdx π π π π − = ∫ ∫ C: 0 sin 0 xdx π = ∫ D: 0 20 2 cos cos xdx xdx π π − 上相应于从变到的一段弧与极轴所围成的图形的面积( ) A: 4 2 3 3 a π B: 3 2 3 4 a π C: 2 3 a π D: 2 3 2a π (11)曲线 cos 2 2 yx x ⎛ ⎞ π π = − ≤≤ ⎜ ⎟ ⎝ ⎠ 与 x 轴所围成的图形绕 x 轴旋转一周而成的旋转体的体积 为( ) A: 2 3 π B: 2 2 π C: 2 π D: 2 2π (12)下列反常积分收敛的是( ) A: 0 sin xdx +∞ ∫ B: 01 2 l 1 dx x − − ∫ C: 1 1 l dx x ∫− D: 0 x e dx − ∫−∞ 三、填空题(将正确答案的序号填写在括号内) (1) ( ) x f x e = 在[0,1] 上的平均值为 (2) ( ) 20 sin 3 cos3 x x dx π + = ∫ (3) 1 2 0 1 1 9 dx x = + ∫ (4) 2 2 3 1 3 1 1 x dx x x + = + − ∫ (5) 2 0 sin 1 cos x dx x π = − ∫

南阳师范学院一数学与统计学院 o5。 当s1时上可女发盖 (8)设f)在0,上连续,frt=1,则f-2x= (9)sinrds= 四、计算题 1.求下列定积分 )-地 hng (3)e5 ④e2产cosd o上4 (6( 2.求下列极限 e2}水p>0 3.求曲线y=x之与x=y2围成的图形的面积 4求函数F(x)=1-4山在[-L,5]上的增减性、极值、凹向及拐点, 五、证明愿 1.设f)在-1,上连线,f)1时,广义积分 a本收缘: 第3页共于页
南阳师范学院—数学与统计学院 第 3 页 共 3 页 (6) 2 4 0 cos xdx x π = ∫ (7) 1 2 0 1 4 5 dx x x = − + ∫ (8)设 f ( ) x 在[0,1] 上连续, 1 0 f () 1 x dx = ∫ ,则 10 f (1 2 ) − x dx = ∫ (9) 2 x sin xdx π −π = ∫ 四、计算题 1. 求下列定积分 (1) 3 1 2 x dx − − ∫ (2) 2 1 11 ln e dx x + x ∫ (3) 41 x e dx ∫ (4) 2 2 0 cos x e xdx π ∫ (5) 2 12 2 dx x x +∞−∞ + + ∫ (6) 1 2 1 1 (ln ) e dx x x − ∫ 2. 求下列极限 (1) 2 2 0 2 0 lim x t x e dt x − → ∫ (2) 1 1 2 lim ( 0) pp p p n n p n →+∞ + ⎛ ⎞ + ++ ⎜ ⎟ > ⎝ ⎠ " 3. 求曲线 2 y = x 与 2 x = y 围成的图形的面积 4. 求函数 0 ( ) ( 4) x F x t t dt = − ∫ 在[−1,5] 上的增减性、极值、凹向及拐点. 五、证明题 1.设 f ( ) x 在[ 1,1] − 上连续,f x( ) 0. 1时,广义积分 2 1 (ln )k dx x x +∞ ∫ 收敛; 当 k ≤1时, 2 1 (ln )k dx x x +∞ ∫ 发散
南阳师范学院一数学与统计学院 《高等数学》第五章一定积分 二。单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码 自测题(A) 填在题干上的括号内.每小题2分,共10分) 题号 五总分 1.设函数fx)在a,上连续,a≤xsb,则下列各式中正确的是() 得分 点孟上a油=国 县f0h=e-. 一.判断题(判断下列各题是否正确,正确的划人,错误的划×,每小题2分,共24分) c&0h=2fe D:dff()=f(d l.若函数f)在a,上连续,x∈a,则fx)迹=。f+C.() 2.若函数fx)在闭区间[a,b上可导,x∈a,b1,则下列等式不一定成立 2.4-Fd=x () 的是() A:ffs达=[/xd B:(ads=/(b)-f(a) 3.曲线y=edh在(-0,0)上是四的,在(0,)上是凸的. () 4.积分sg如迹可以直接使用牛倾莱布尼兹公式求出 C: () 法e=国 D:C-f四 3.阿基米德螺线p=a(a>0)上0=0到0=2π的弧长是() s=(传…引a () A:a+odo B:["aodo &0 sffiomous得 () C:av+o do D:+0d0 7如果矿点女=1则=2 () 4若x和是f)的一个原函数,则fx达=() &.如果Fm是f)的原函数,则efe)在=Fb-Fa. () A:1+e B:I-e C:e D:-e 9当P≤1时,反常积分广女与女都收敛 5.若函数f(x)在闭区间[-a,a上都连续,则下列等式成立的是() () 10.若函数f)在[a,上连线,则心2x本=fud0. A:f(xyix=0.B:f(xix=[[f(x)+f(x () C:f(=2[f(x D:(s=f(x)-f(-x) l.当x→0时,sind是r的高阶无穷小, () () 第1页共2页
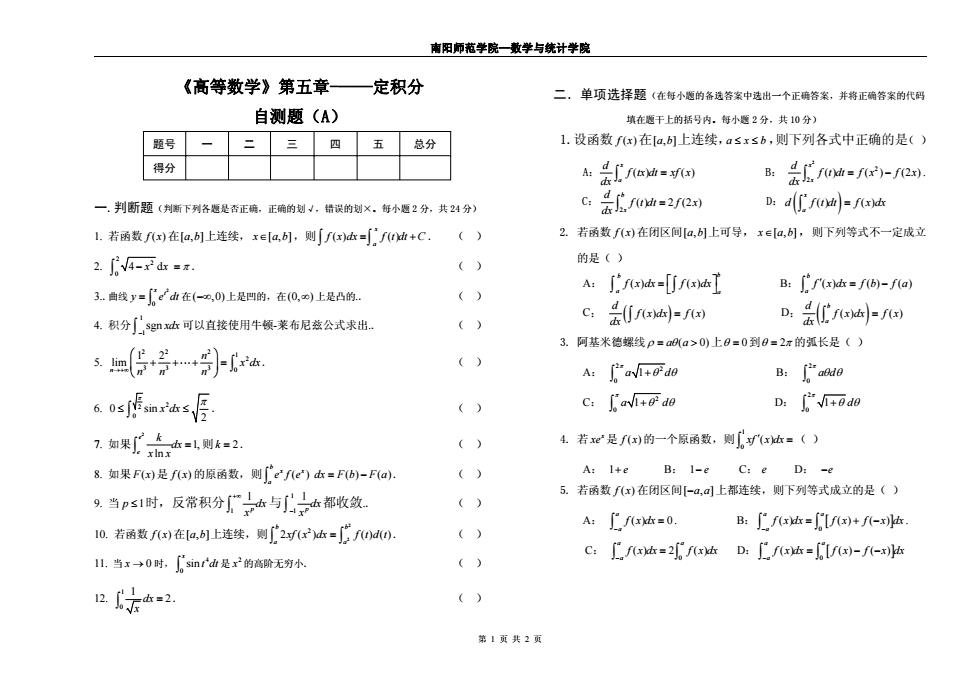
南阳师范学院—数学与统计学院 第 1 页 共 2 页 《高等数学》第五章-——定积分 自测题(A) 题号 一 二 三 四 五 总分 得分 一.判断题(判断下列各题是否正确,正确的划√,错误的划×。每小题 2 分,共 24 分) 1. 若函数 f ( ) x 在[,] a b 上连续, x∈[,] a b ,则 ( ) () x a f x dx f t dt C = + ∫ ∫ . () 2. 2 2 0 4 d − = x x π ∫ . () 3..曲线 2 0 x t y = e dt ∫ 在( , 0) −∞ 上是凹的,在(0, ) ∞ 上是凸的.. () 4. 积分 1 1sgn xdx ∫ − 可以直接使用牛顿-莱布尼兹公式求出.. () 5. 22 2 1 2 33 3 0 1 2 lim n n x dx →+∞ nn n ⎛ ⎞ ⎜ ⎟ + +⋅⋅⋅+ = ⎝ ⎠ ∫ . () 6. 2 2 0 0 sin 2 x dx π π ≤ ≤ ∫ . () 7. 如果 2 1, ln e e k dx x x = ∫ 则k = 2 . () 8. 如果 F x( )是 f ( ) x 的原函数,则 ( ) () () b x x a e f e dx F b F a = − ∫ . () 9. 当 p ≤1时,反常积分 1 lp dx x +∞ ∫ 与 11 lp dx x ∫ − 都收敛.. () 10. 若函数 f ( ) x 在[,] a b 上连续,则 2 2 2 2 ( ) () () b b a a xf x dx f t d t = ∫ ∫ . () 11. 当 x → 0 时, 4 0 sin x t dt ∫ 是 2 x 的高阶无穷小. () 12. 1 0 1 dx 2 x = ∫ . () 二.单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码 填在题干上的括号内。每小题 2 分,共 10 分) 1.设函数 f ( ) x 在[,] a b 上连续,axb ≤ ≤ ,则下列各式中正确的是( ) A: ( ) () x a d f tx dt xf x dx = ∫ B: 2 2 2 ( ) ( ) (2 ) xx d f t dt f x f x dx = − ∫ . C: 2 ( ) 2 (2 ) b x d f t dt f x dx = ∫ D: ( ) () ( ) xa d f t dt f x dx = ∫ 2. 若函数 f ( ) x 在闭区间[,] a b 上可导, x∈[,] a b ,则下列等式不一定成立 的是( ) A: () () b b a a f x dx f x dx = ⎡ ⎤ ∫ ∫⎣ ⎦ B: () () () ba f ′ x dx f b f a = − ∫ C: ( () () ) d f x dx f x dx = ∫ D: ( ) () () ba d f x dx f x dx = ∫ 3. 阿基米德螺线 ρ = a a θ ( 0) > 上θ = 0到θ = 2π 的弧长是( ) A: 2 2 0 a d 1 π +θ θ ∫ B: 20 a d π θ θ ∫ C: 2 0 a d 1 π +θ θ ∫ D: 20 1 d π +θ θ ∫ 4. 若 x xe 是 f ( ) x 的一个原函数,则 10 xf x dx ′( ) = ∫ ( ) A: 1+ e B: 1− e C: e D: −e 5. 若函数 f ( ) x 在闭区间[ ,] −a a 上都连续,则下列等式成立的是( ) A: () 0 a a f x dx − = ∫ . B: [ ] 0 () () ( ) a a a f x dx f x f x dx − = +− ∫ ∫ . C: 0 () 2 () a a a f x dx f x dx − = ∫ ∫ D: [ ] 0 () () ( ) a a a f x dx f x f x dx − = −− ∫ ∫

南阳师范学院一数学与统计学院 三.填空题(将正确答案填写在空格上,每小题2分,共2分) 4.设函数(x)=[(1-1h.求 1.f(x)=sinx在-x,]上的平均值为 (1)求函数④(x)的单调区间(5分) du J。1+L= (2)求函数D(x)的极值(3分) (3)求函数(x)在0,2]上的最值(3分) 五求参数方程-<在1=0时相胺点处的切线方程(5分) 4.若fx)在0,上连续,fx达=l,则f0-x达= y=cost. 5.若∫fxd=e+C,则f(sinx)cosxd= 五、证明题(共16分) 1.设f田)在-1,川上连线,f田)<0.证明方程x-工fh=0在(-1,山有且仅 有一个根.(5分) 2.若函数fx)在闭区间[a,b]上连续.,x∈a,小.证明D(x)=f(是函数 四、计算题(共38分) f(x)的原函数,且D'(x)=fx)(5分) 1.求下列定积分(每小题3分,共12分) 3.若函数f(x)在区间(-力,+m)上连续,证明: )sim妆 (1)当f(x)为奇函数时,函数f出为偶函数.(3分) (3)[xlnxdr ④子 (2)当f)为偶函数时,f0出为奇函数.(3分) t-sint)dt 2.求极限Iim三 (5分) arcsintd 3.求曲线y=x之与直线y=2x围成的图形的面积(5分) 第2页共2页
南阳师范学院—数学与统计学院 第 2 页 共 2 页 三.填空题(将正确答案填写在空格上,每小题 2 分,共 12 分) 1. f ( ) sin x x = 在[ ,] −π π 上的平均值为 2. 0 1 1 lim x x du u → x + = ∫ 3. 999 1 2 11 x dx x − = + ∫ 4. 若 f ( ) x 在[0,1] 上连续, 1 0 f () 1 x dx = ∫ ,则 10 f (1 ) − x dx = ∫ 5.若 2 ( ) x f x dx e C = + ∫ ,则 20 f (sin ) cos x xdx π = ∫ 6. 1 4 0 2 1 1 4 dx x = − ∫ . 四、计算题(共 38 分) 1. 求下列定积分(每小题 3 分,共 12 分) (1) sin x dx π∫−π (2) 2 2 4 36 cos xdx x π ∫ π (3) 1 ln e x xdx ∫ (4) 2 0 1 1 dx x ∞ + ∫ 2. 求极限 2 0 0 0 ( sin ) lim arcsin x x x t t t dt tdt → + − ∫ ∫ (5 分) 3. 求曲线 2 y = x 与直线 y x = 2 围成的图形的面积(5 分) 4. 设函数 1 ( ) ( 1) x Φ= − x t t dt ∫ .求 (1)求函数Φ( ) x 的单调区间(5 分) (2)求函数Φ( ) x 的极值(3 分) (3)求函数Φ( ) x 在[0, 2]上的最值(3 分) 5. 求参数方程 2 0 , cos . t u x e du y t ⎧⎪ = ⎨⎪⎩ =∫ 在t = 0时相应点处的切线方程. (5 分) 五、证明题(共 16 分) 1.设 f ( ) x 在[ 1,1] − 上连续,f x( ) 0. < 证明方程 1 () 0 x x f t dt − − = ∫ 在( 1,1) − 有且仅 有一个根. (5 分) 2. 若函数 f ( ) x 在闭区间[,] a b 上连续., x∈[ , ]. a b 证明 ( ) () x a Φ = x f t dt ∫ 是函数 f ( ) x 的原函数,且Φ′() () x = f x (5 分) 3. 若函数 f ( ) x 在区间(, ) −∞ +∞ 上连续,证明: (1)当 f ( ) x 为奇函数时,函数 0 ( ) x f t dt ∫ 为偶函数.(3 分) (2)当 f ( ) x 为偶函数时, 0 ( ) x f t dt ∫ 为奇函数. (3 分)
南阳师范学院一戴学与统计学院 二单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码 《高等数学》第五章一定积分 填在题干上的括号内。每小题2分,共10分) 自测题(B) L.设函数fx)在Ia,b]上连续,asx≤sb,则下列各式中正确的是() 题号 三四 五总分 A云引ah=e 云0h=f-2, 得分 c孟oh=2 D:d(f.f)=f(ds 一.判断题(判新下列各题是香正确,正确的划,错误的划×,每小题2分,共24分) 2.若函数fx)在闭区间[a,上可导,x∈a,,则下列等式不一定成立 1.若函数f)在a,上连续,x∈a,,则町fx达=fh+C.() 的是() 2.V9-子山=9z () A∫fx达=可fx[ B:f(x)d=f(b)-f(a) 3.曲线y=d山在(-,0)上是四的,在0,+)上是凸的, () C: (fr)) C 4.积分广kos女可以直接使用牛顿-莱布尼兹公式求出, () 3.摆线-c:一损0≤1s2的长是() y=t-sint 5=(告品别p> () 广+e-md B:V+(cos吓ah 6.Inxdes (Inds. () C:cosidr D:cosi dr 五如果广三女=则k=子 () 4.若fm的导数是e,则心fx达=() 8.如果F)是f)的原函数,则efe)d=Fb)-Fa. () A:Ite B:1-e C:e D:e g当p>1时,反常积分子女收敛 () 5.若函数f(x)在闭区间[-a,a上都连续,则下列等式成立的是() 10.若函数fx)在a,上连续,则广3x2f2d=心fud). () A:f(=0. B:=f[f(3)+f( 11.当x→0时,smd是2的高阶无穷小 () C:f(=2(D:f(s=f[f(x)-/( 22 () 第1页共2页
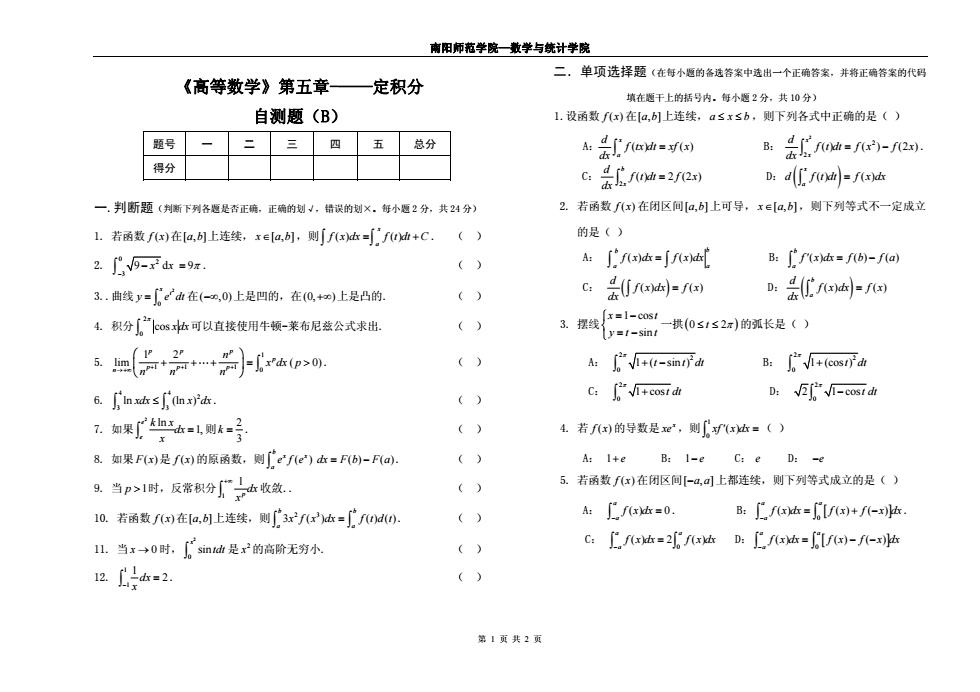
南阳师范学院—数学与统计学院 《高等数学》第五章-——定积分 自测题(B) 第 1 页 共 2 页 题号 一 二 三 四 五 总分 得分 一.判断题(判断下列各题是否正确,正确的划√,错误的划×。每小题 2 分,共 24 分) 1. 若函数 f ( ) x 在 上连续, [,] a b x[,] a b ,则 ( ) () x a f x dx f t dt C . ( ) 2. 0 3 9 d2 x x 9 2t y ( (0, ) . ( ) 3..曲线 dt 在 上是凹的,在 0 x e ,0) 上是凸的. ( ) 4. 积分 2 0 cos xdx 可以直接使用牛顿-莱布尼兹公式求出. ( ) 5. 1 1 0 ( 0) p x dx p 2 (ln ) 1 1 1 2 lim pp p pp p n n nn n . ( ) 6. 4 4 3 3 ln xdx x dx . ( ) 7. 如果 2 e e ln dx x 1, k x 则 23 k () ( . ( ) 8. 如果 是 F x f x) ( ) () ( x x e dx F b F a 1 的原函数,则 ) . ( ) b a e f 9. 当 p 时,反常积分 1 lp dx x ( ) 收敛.. ( ) 10. 若函数 f x [ , 2 3 在 上连续,则 a b] 3 ( ) () ( ) b b a a x f x dx f t d t 2 0 sin x tdt 2 . ( ) 11. 当 时, 是 x 0 x 的高阶无穷小. ( ) 12. 1 1 1 dx 2 x ( ) . ( ) 二.单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码 填在题干上的括号内。每小题 2 分,共 10 分) f x 在[ , a b]上连续,a x b ,则下列各式中正确的是( ) 1.设函数 A: ( ) ( x a d f tx dt xf x) dx B: 2 2 2 ( ) ( ) (2 ) xx d f t dt f x f x dx . C: 2 b x d f ( ) 2 (2 ) t dt f x () ( ) xa d f t dt f x ( ) dx D: dx 2. 若函数 f x 在闭区间[ , a b]上可导, x[,] a b ,则下列等式不一定成立 的是( ) A: ( ) b a ( ) b a f x d x f x dx () () ( ba B: f x dx f b f a ) C: () () d f x dx f x dx D: () ( ba d f x dx f x) dx 1 cos sin x t 3. 摆线 y t t 一拱0 2 t 的弧长是( ) A: 2 2 0 1 ( sin ) t t dt B: 2 2 0 1 (cos )t d t C: 2 0 1 cost dt D: 20 2 1 cost dt ( ) x xe 1 0 4. 若 f x 的导数是 ,则 xf x dx ( ) 1 e ( ) B: 1 e C: e D: e ( ) A: f x 在闭区间[ , a a]上都连续,则下列等式成立的是( ) 5. 若函数 A: ( ) 0 a a f x 0 () () ( ) a a a dx . B: f x dx f x f x dx 0 2 () . C: ( ) a a a f x d x f x dx 0 () () ( ) a a a D: f x dx f x f x dx

南阳师范学院一数学与统计学院 三.填空题(将正确答案填写在空格上,每小题2分,共12分) 4.设函数(x)=[广1-1h.求 1.f(x)=cosx在-x,x]上的平均值为 (1)求函数④x)的单调区间(5分) In(1+u)du (2)求函数D(x)的极值(3分) 2. (3)求函数(x)在0,2】上的最值(3分) 3 5.求由c山+cosd=0所确定的隐函数在(子n2]处的切线方程 4.若f)在0,上连续,fx本=l,则f-xk= (5分) 5.若∫fx)=e+C,则后f(cosx)sin xd= 五、证明愿(共16分) 6 上证期方程3-品-0在0)有隆一的实是(6分》 2.若函数fx)在闭区间[a,上连续.,x∈a,b1 四、计算题(共38分) 证明:(x)=f0)h是函数f)的原函数,且Φ)=f田)(5分) 1.求下列定积分(每小题3分,共12分) 3.若函数fx)在区间(-中,+o)上连续。 (1)[sgnsd (2)[e5 证明:当fx)为奇函数时,函数f出为偶函数.当fx)为偶函 (3)e产sint (4) 数时,f)h为奇函数.(6分) t(t-sint)dr (5分) 3.求曲线y=x2与x=y2围成的图形的面积(5分) 第2页共2页
证明: ( ) () x a x f t dt 是函数 f ( ) x 的原函数,且 () () x f x (5 分) 5. 求由 0 0 cos 0 y x t e dt tdt 所确定的隐函数在 ,ln 2 2 处的切线方程. (5 分) 证明:当 f ( ) x 为奇函数时,函数 0 ( ) x f t dt 为偶函数。当 f ( ) x 为偶函 数时, 0 ( ) x f t dt 为奇函数.(6 分) 南阳师范学院—数学与统计学院 第 2 页 共 2 页 三.填空题(将正确答案填写在空格上,每小题 2 分,共 12 分) 1. f ( ) cos x x 在[ , ]上的平均值为 2. 0 2 0 ln(1 ) lim x x u du x 3. 2013 1 2 11 x dx x 4. 若 f ( ) x 在 上连续, [0,1] 10 f () 1 x dx ,则 10 f (1 ) x dx 5.若 2 ( ) x f x dx e C ,则 20 f (cos )sin x xdx 6. 1 6 0 2 1 1 9 dx x . 四、计算题(共 38 分) 1. 求下列定积分(每小题 3 分,共 12 分) (1) 1 1sgn xdx (2) 41 x e dx (3) (4) 2 2 0 sin x e xdx 2 12 2 dx x x 2. 求极限 2 0 0 0 ( sin ) lim arcsin x x x t t t dt tdt (5 分) 3. 求曲线 2 y x 与 2 x y 围成的图形的面积(5 分) 4. 设函数 1 ( ) ( 1) x x t t dt .求 (1)求函数( ) x 的单调区间(5 分) (2)求函数( ) x 的极值(3 分) (3)求函数( ) x 在 上的最值(3 分) [0,2] 五、证明题(共 16 分) 1.证明:方程 2 0 3 1 0 1x dt x t 在 有唯一的实根. (5 分) (0,1) 2. 若函数 f ( ) x 在闭区间 上连续., [,] a b x[ , ]. a b 3. 若函数 f ( ) x 在区间(,) 上连续,