
第一节定积分的概念与性质 问题的提出 二、定积分的定义 三、定积分的几何意义 四、定积分的性质
第一节 定积分的概念与性质 一、问题的提出 二、定积分的定义 三、定积分的几何意义 四、定积分的性质
问题的提出:怎么求不规则几何图形的面积? 化整为零化不规则为规则物罐方法 曹冲称象法 v=x2 爱迪生测灯泡法 求极限 一天, 巴一只灯泡交给他的助手阿普 顿,要他 4=im∑矩形容积,阿普顿拿着灯炮琢磨 了好长时间,于是用皮尺在灯泡上左右、上下量了一 阵,又在纸上画了好多的草图,写满了各种尺寸,列 了许多道算式,算来算去还未有个结果。爱迪生见他 算得满头大汗,就对他说:“我的上帝,你还是用这 个方法算吧!”他在灯泡里倒满了水递给阿普顿说: “把这些水倒进量杯里,看一看它的体积,就是灯泡 的容积了
面积=? 0 a 曲边三角形 y=x2 怎么求不规则几何图形的面积? 曹冲称象法 爱迪生测灯泡法 化整为零 化不规则为规则 数学方法 物理 求极限 一天,发明家爱迪生把一只灯泡交给他的助手阿普 顿,要他算出玻璃灯泡的容积,阿普顿拿着灯炮琢磨 了好长时间,于是用皮尺在灯泡上左右、上下量了一 阵,又在纸上画了好多的草图,写满了各种尺寸,列 了许多道算式,算来算去还未有个结果。爱迪生见他 算得满头大汗,就对他说:“我的上帝,你还是用这 个方法算吧!”他在灯泡里倒满了水递给阿普顿说: “把这些水倒进量杯里,看一看它的体积,就是灯泡 的容积了。” 一、问题的提出: n i A i 1 矩 形 n i A i 1 lim 矩 形
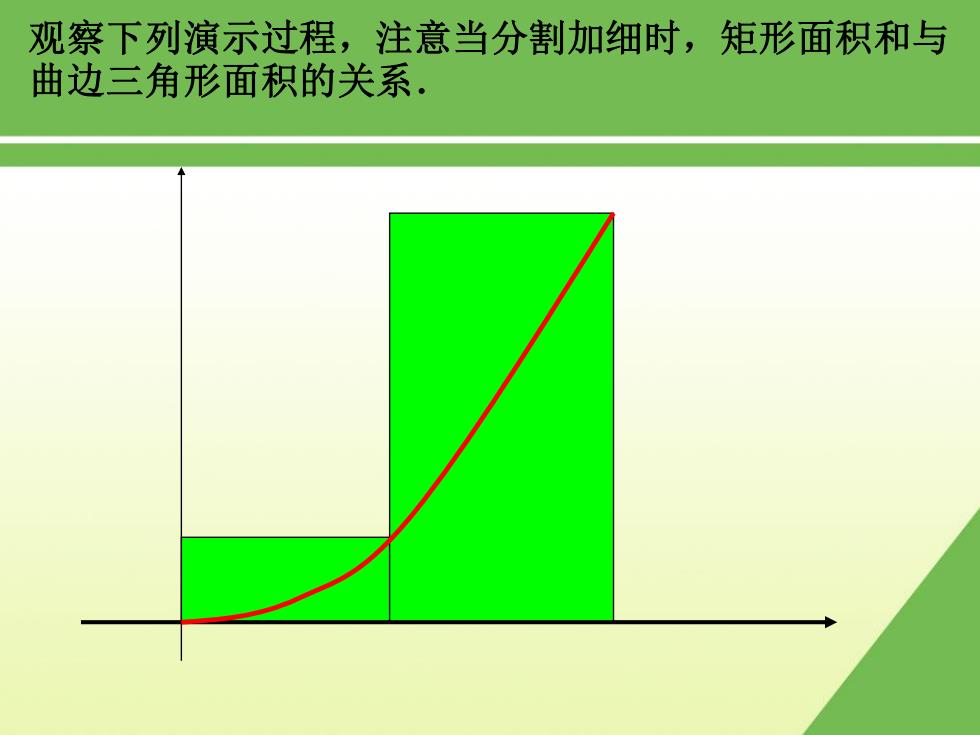
观察下列演示过程,注意当分割加细时,矩形面积和与 曲边三角形面积的关系
观察下列演示过程,注意当分割加细时,矩形面积和与 曲边三角形面积的关系.
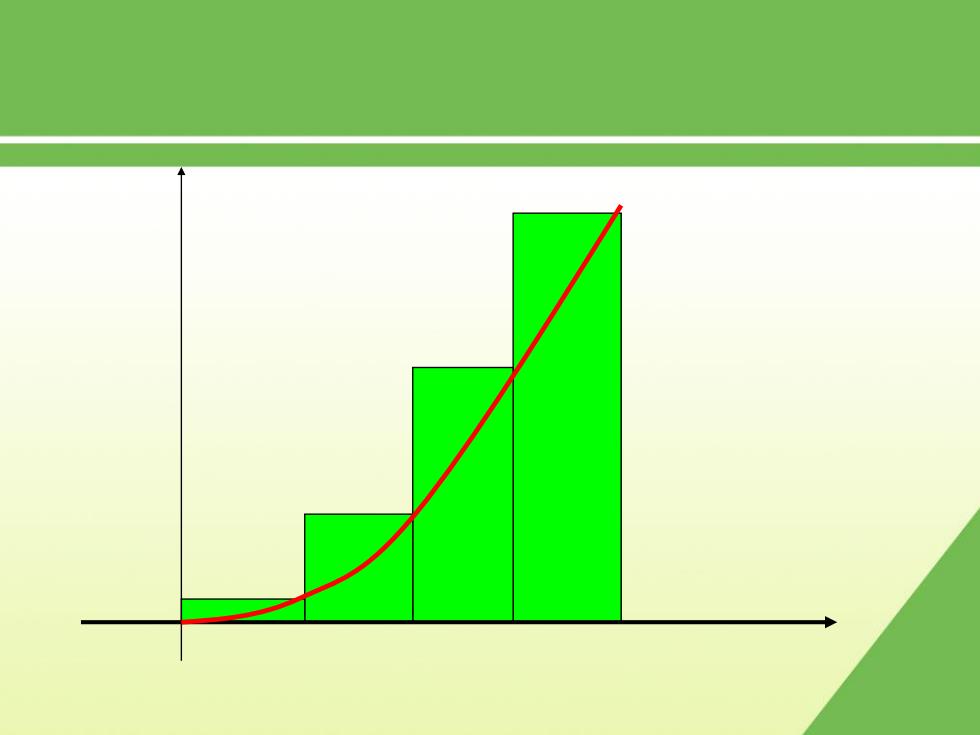
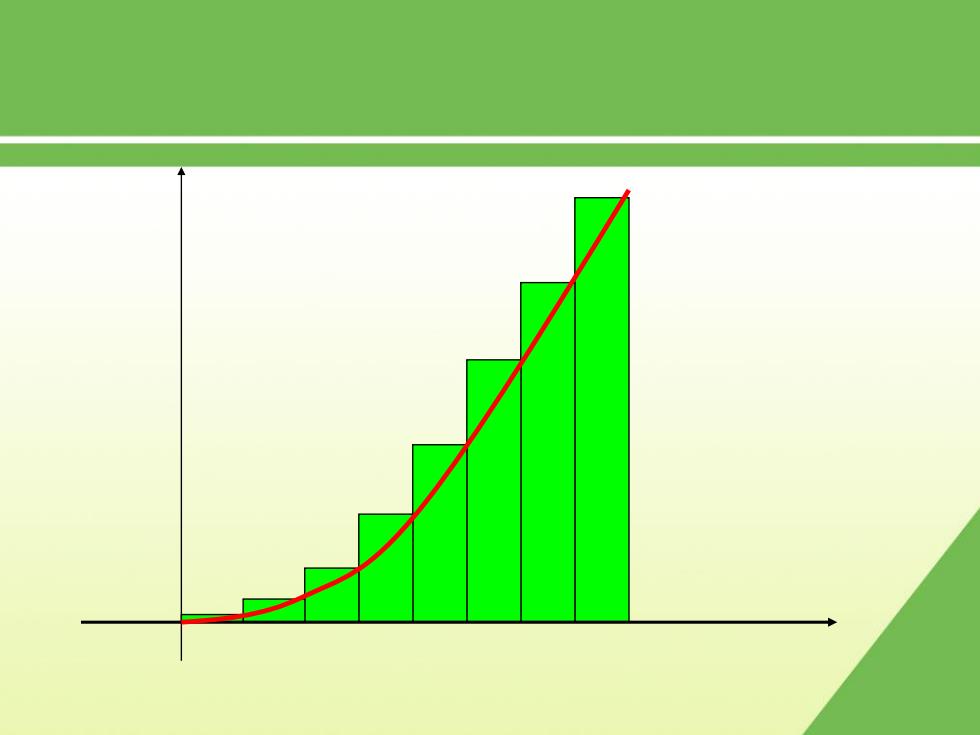
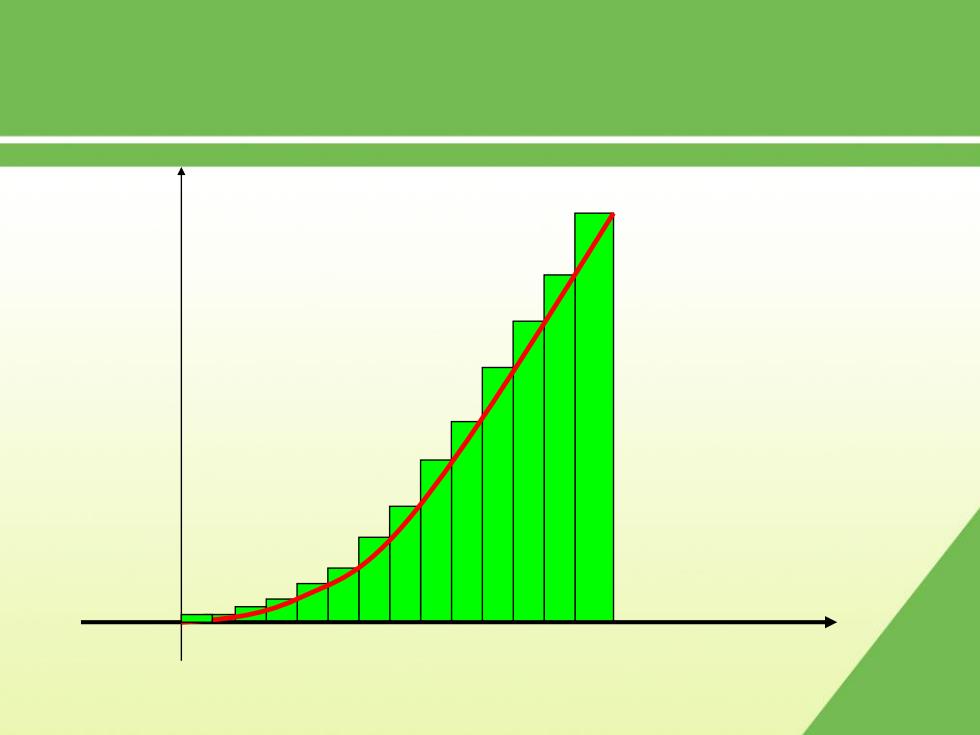

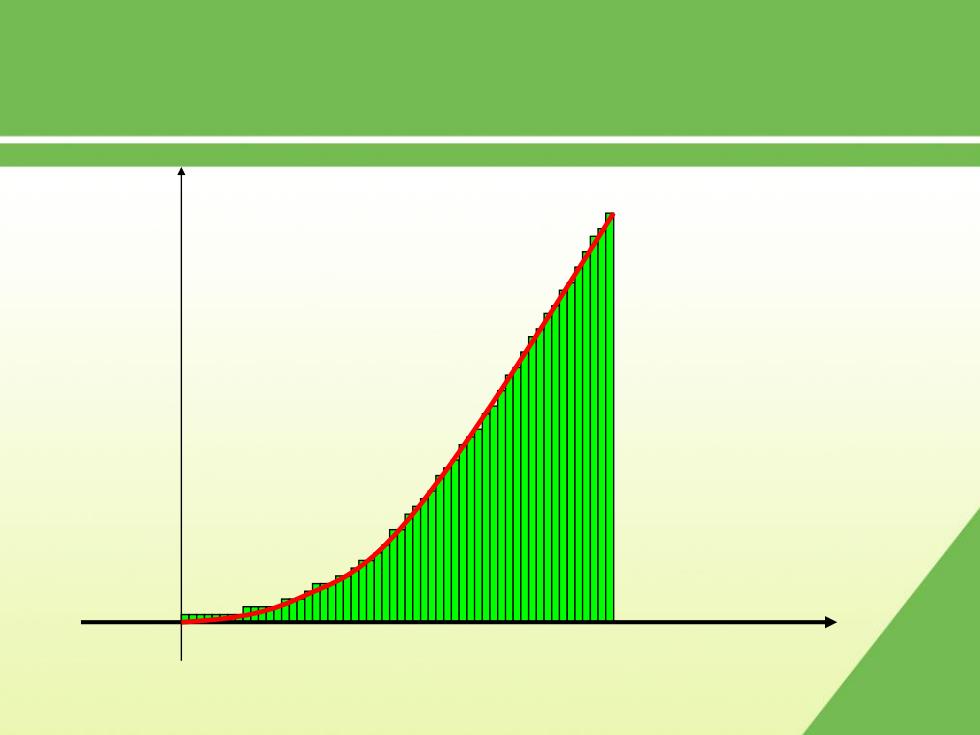
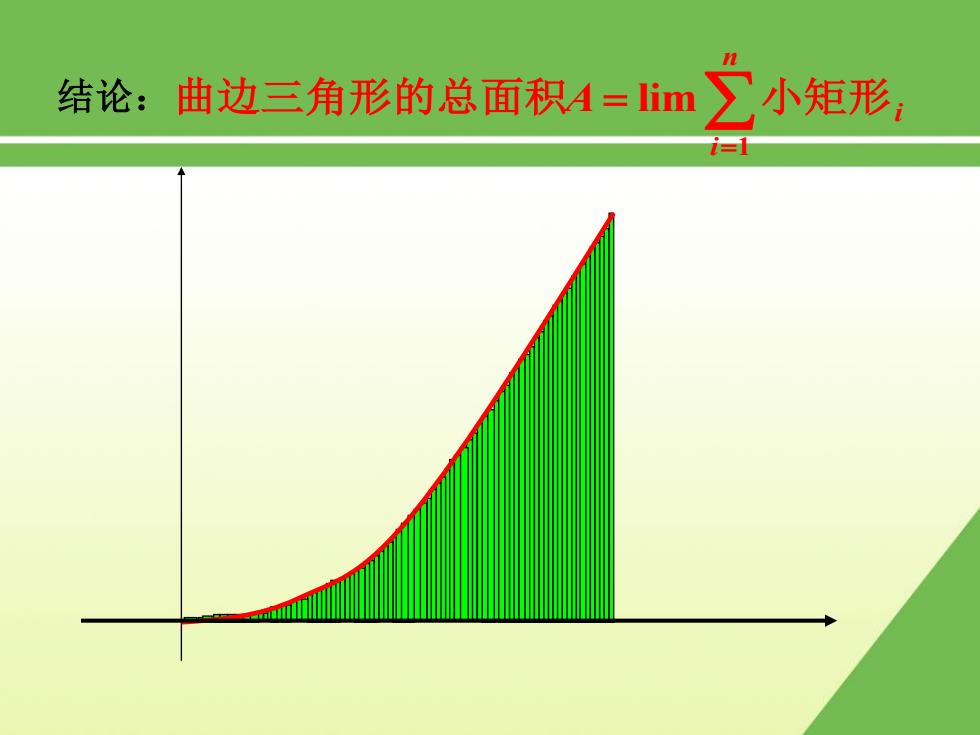
结论:曲边三角形的总面积A=im 小矩形: i=1
n i A i 1 结论: 曲边三角形的总面积 lim 小矩形
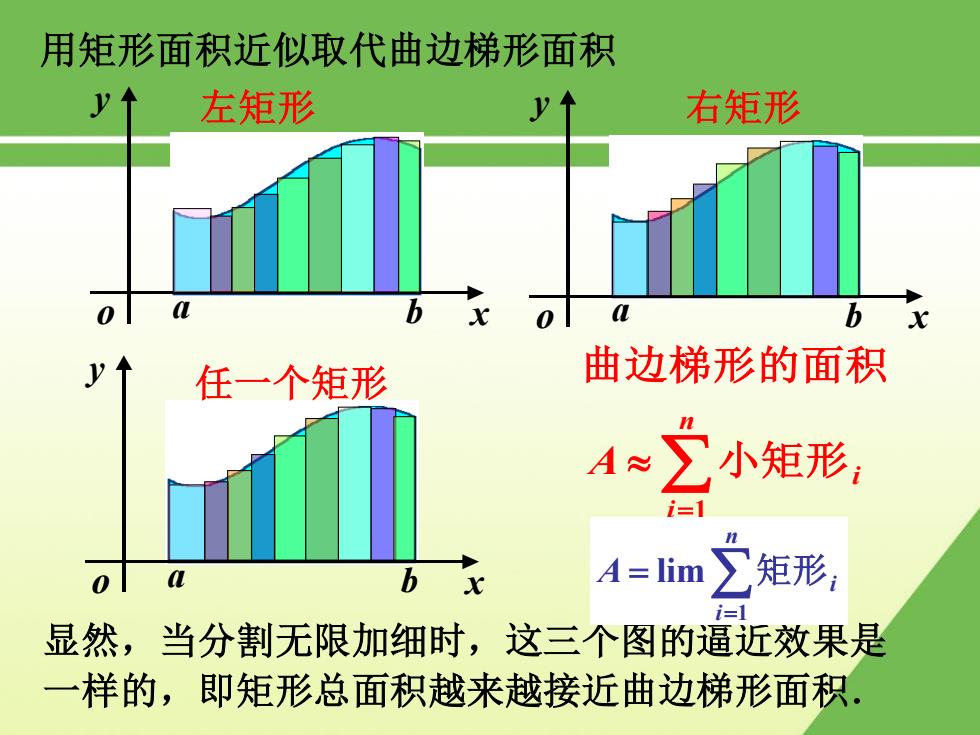
用矩形面积近似取代曲边梯形面积 左矩形 右矩形 0 L 任一个矩形 曲边梯形的面积 A≈ ∑小矩形, i= 0 L 4=lim 矩形 i=1 显然,当分割无限加细时,这三个图的逼近效果是 一样的,即矩形总面积越来越接近曲边梯形面积
a b x y o 用矩形面积近似取代曲边梯形面积 显然,当分割无限加细时,这三个图的逼近效果是 一样的,即矩形总面积越来越接近曲边梯形面积. a b x y o a b x y o 左矩形 右矩形 任一个矩形 n i A i 1 小矩形 曲边梯形的面积 n i A i 1 lim 矩形