
第三节格林公式及其应用 一、格林公式 二、平面上曲线积分与路径无关的条件 三、二元函数的全微分求积
一、格林公式 二、平面上曲线积分与路径无关的条件 三、二元函数的全微分求积 第三节 格林公式及其应用
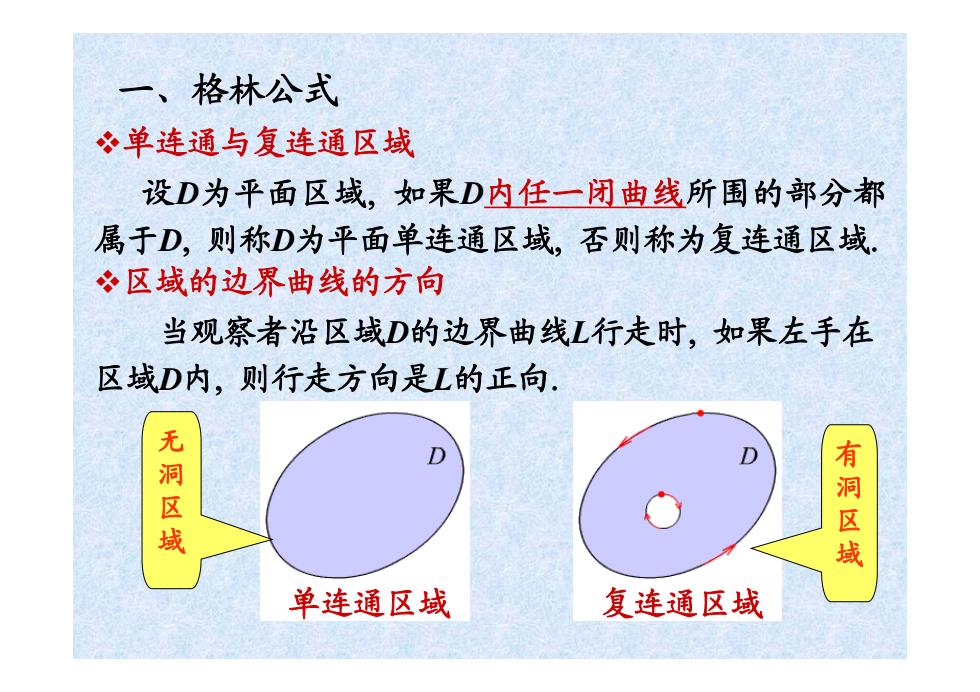
一、格林公式 ·单连通与复连通区域 设D为平面区域,如果D内任一闭曲线所围的部分都 属于D,则称D为平面单连通区域,否则称为复连通区域。 ?区域的边界曲线的方向 当观察者沿区域D的边界曲线L行走时,如果左手在 区域D内,则行走方向是L的正向 无洞区域 D D 有洞区域 单连通区域 复连通区域
一、格林公式 单连通与复连通区域 区域的边界曲线的方向 当观察者沿区域D的边界曲线L行走时, 如果左手在 区域D内, 则行走方向是L的正向. 单连通区域 复连通区域 设D为平面区域, 如果D内任一闭曲线所围的部分都 属于D, 则称D为平面单连通区域, 否则称为复连通区域. 无 洞 区 域 有 洞 区 域

必定理1 设闭区域D由分段光滑的曲线L围成,函数P,y及 2,以在D上具有一阶连续偏导数,则有 小器器hPh+0一格林公式 其中L是D的取正向的边界曲线: 注:格林公式反映的是二重积分和第二类曲线积 分的关系
∫∫ ∫ = + ∂∂ − ∂∂ L D dxdy Pdx Qdy y P x Q( ) , 定理1 设闭区域D由分段光滑的曲线L围成, 函数P(x, y)及 Q(x, y)在D上具有一阶连续偏导数, 则有 其中L是D的取正向的边界曲线. ——格林公式 注:格林公式反映的是二重积分和第二类曲线积 分的关系

证明:1)若D既是X型区域,又是Y型区域,且 p1(x)≤y≤p2(x) ↑y E d a≤x≤b 4(y)≤x≤W2(y) C c≤y≤d 2a,-装 则 -Q(v2().y)dy-[Q((y).y)dy -ae0xMy-∫cac(x,Hy =∫eQx,y+∫acx,y
证明: 1) 若D 既是 X 型区域 , 又是 Y 型区域 , 且 ⎩ ⎨ ⎧ ≤ ≤ ≤ ≤ a x b x y x D ( ) ( ) : ϕ1 ϕ 2 ⎩ ⎨ ⎧ ≤ ≤ ≤ ≤ c y d y x y D ( ) ( ) : ψ 1 ψ 2 则 x y x Q D d d ∫∫ ∂ ∂ ∫ = d c Q ( ( y), y ) d y ψ 2 ∫ ∂ ( ) ∂ ( ) 2 1 d y y x x ψ Q ψ ∫ = CBE Q ( x, y ) d y ∫ − CAE Q ( x, y ) d y ∫ = CBE Q ( x, y ) d y ∫ + EAC Q ( x, y ) d y ∫ − d c Q ( ( y), y ) d y ψ 1 ∫ = d c d y d c y o x E C A B a b D

即 儿器dd. ① 同理可证 -d-,a ② ①、②两式相加得: n是adv-fH+
即 x y x Q D d d ∫∫ ∂∂ ∫ = LQ(x, y)dy 同理可证 x y y P D d d ∫∫ ∂∂ − ∫ = L P(x, y)dx ① ② ①、②两式相加得: ( ) ∫∫ ∫ = + ∂∂ − ∂∂ D L x y P x Q y yP xQ d d d d

2)若D不满足以上条件,则可通过加辅助线将其分割 为有限个上述形式的区域,如图 U(是 -2n器影, k=1 X 2ma+QaaD表示D,的正向边剂 =f Pdx+Qdy
y o x L 2) 若D不满足以上条件, 则可通过加辅助线将其分割 D1 Dn D2 ∑ ( ) ∫∫ = ∂ ∂ − ∂ ∂ = n k D x y y P x Q k 1 d d ( ) x y y P x Q D d d ∂ ∂ − ∂ ∂ ∫∫ ∑∫ = ∂ = + n k Dk P x Q y 1 d d ∫ = + L Pdx Qdy 为有限个上述形式的区域 , 如图 ( 表示 的正向边界) Dk Dk ∂
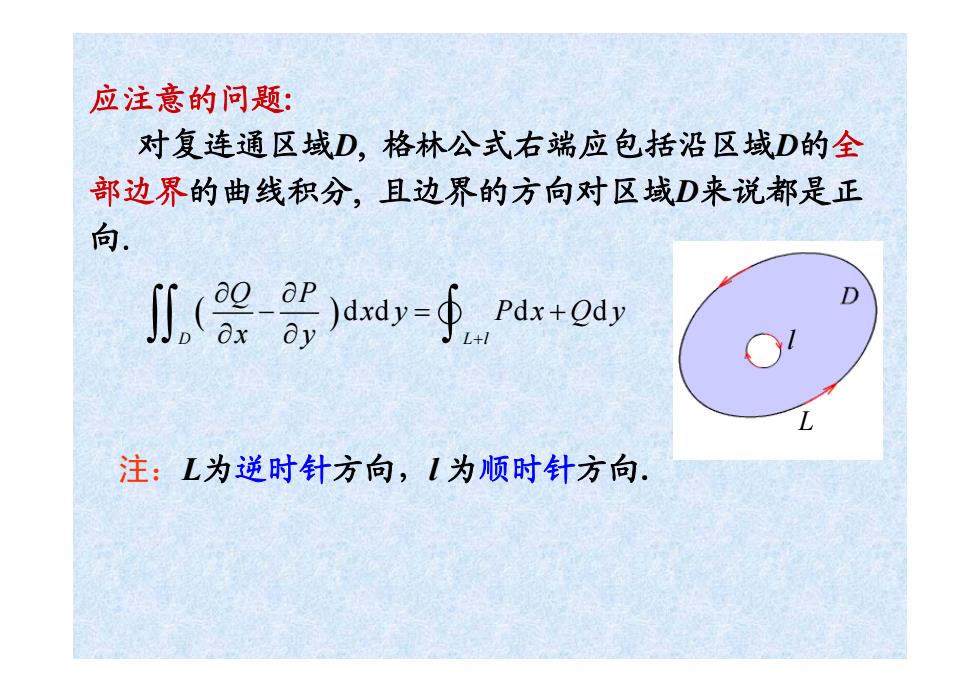
应注意的问题: 对复连通区域D,格林公式右端应包括沿区域D的全 部边界的曲线积分,且边界的方向对区域D来说都是正 向 八(晨udvf,Pr+ou D 注:L为逆时针方向,1为顺时针方向
应注意的问题: 对复连通区域D, 格林公式右端应包括沿区域D的全 部边界的曲线积分, 且边界的方向对区域D来说都是正 向. L l ( ) dd d d D Ll Q P xy Px Qy x y + ∂ ∂ − =+ ∫∫ ∫ ∂ ∂ v 注:L为逆时针方向,l 为顺时针方向

格林公式: I小器d-fr+ow 冬用格林公式计算区域的面积 设区域D的边界曲线为L,则D的面积为 A-5-d 提示:在格林公式中,令P=y,Q=x,则有 重-+d=2可,或A川=-
提示: 格林公式: 用格林公式计算区域的面积 ∫∫ ∫ = + ∂∂ − ∂∂ L D dxdy Pdx Qdy y P x Q( ) . 设区域D的边界曲线为L, 则D的面积为 ∫ ∫∫ − + = D L ydx xdy 2 dxdy , 在格林公式中, 令P=−y, Q=x, 则有 ∫ = − L A xdy ydx 21 . 或 ∫∫ ∫ = = − L D A dxdy xdy ydx 21

?用格林公式计算区域的面积 A=5- 例1求椭圆=cos8,Jy=bsin0所围成图形的面积A. 解设L是由椭圆曲线,则 A(absin20+abcos20do -abfdo-abz
例1 求椭圆x=acosθ, y=bsinθ 所围成图形的面积A. 解 设L是由椭圆曲线, 则 ∫ = − L A xdy ydx 21 θ π = ab d ∫2 2 0 1 ∫ = + π θ θ θ 20 2 2 ( sin cos ) 21 ab ab d =abπ . 用格林公式计算区域的面积 ∫ = − L A xdy ydx 21

例2计算jedd,其中D是以00,0,A1,1),B0,1) D 为顶,点的三角形闭区域。 B 00_op=ey 解令P=0,Q=xey,则xy D 因此,由格林公式有 j∬erdd-∫xerd 0A+AB+BO ∫xedy-ek=l-e 提示: 要使0邓=e,只需P-0,Q=ey. Ox Oy
因此, 由格林公式有 解 提示: 要使 2 y e y P x Q − = ∂ ∂ − ∂ ∂ , 只需 P=0, 2 y Q xe− = . 为顶点的三角形闭区域. 例 2 计算∫∫ − D y e dxdy 2 , 其中D 是以O(0, 0), A(1, 1), B(0, 1) 1 0 2 − =∫ xe dx x (1 ) 21 −1 = −e . 令P=0, 2 y Q xe− = , 则 2 y e yP xQ − = ∂∂ − ∂∂ . ∫ ∫∫ + + − − = OA AB BO y D y e dxdy xe dy 2 2 2 e d y OA x y − = ∫