
目录 第三章矩阵的初等变换与线性方程组 ◆第一节 向量组及其线性组合 ◆第二节 向量组的线性相关性 ◆第三节 向量组的秩 ◆第四节 线性方程组解的结构 ◆第五节 向量空间
目 录 第三章矩阵的初等变换与线性方程组 第一节 向量组及其线性组合 第二节 向量组的线性相关性 第三节 向量组的秩 第四节 线性方程组解的结构 第五节 向量空间

学习基本要求 第四章向量组的线性相关性 ◆1.理解n维向量、向量的线性组合与线性表示的概念 ◆2.理解向量组线性相关、线性无关的概念,掌握向量 组线性相关、线性无关的有关性质及判别法, ◆3.理解向量组的极大线性无关组和向量组的秩的概 念,会求向量组的极大线性无关组及秩, ◆4.理解向量组等价的概念,理解矩阵的秩与其行(列) 向量组的秩之间的关系, ◆5.了解n维向量空间、子空间、基底、维数、坐标等 概念. ◆6.了解基变换和坐标变换公式,会求过渡矩阵 ◆7.理解齐次线性方程组的基础解系、通解及解空间的 概念,掌握齐次线性方程组的基础解系和通解的求法. ◆8.理解非齐次线性方程组解的结构及通解的概念 ◆9.掌握用初等行变换求解线性方程组的方法
学习基本要求 第四章 向量组的线性相关性 1.理解n维向量、向量的线性组合与线性表示的概念. 2.理解向量组线性相关、线性无关的概念,掌握向量 组线性相关、线性无关的有关性质及判别法. 3.理解向量组的极大线性无关组和向量组的秩的概 念,会求向量组的极大线性无关组及秩. 4.理解向量组等价的概念,理解矩阵的秩与其行(列) 向量组的秩之间的关系. 5.了解n维向量空间、子空间、基底、维数、坐标等 概念. 6.了解基变换和坐标变换公式,会求过渡矩阵. 7.理解齐次线性方程组的基础解系、通解及解空间的 概念,掌握齐次线性方程组的基础解系和通解的求法 . 8.理解非齐次线性方程组解的结构及通解的概念. 9.掌握用初等行变换求解线性方程组的方法.

学习考研要求第三章矩阵的初等变换与线性方程组 ◆1.理解n维向量、向量的线性组合与线性表示的概念 ◆2.理解向量组线性相关、线性无关的概念,掌握向量 组线性相关、线性无关的有关性质及判别法 ◆3.理解向量组的极大线性无关组和向量组的秩的概 念,会求向量组的极大线性无关组及秩 ◆4.理解向量组等价的概念,理解矩阵的秩与其行(列) 向量组的秩之间的关系. ◆5.了解维向量空间、子空间、基底、维数、坐标等 概念. ◆6.了解基变换和坐标变换公式,会求过渡矩阵 ◆7.理解齐次线性方程组的基础解系、通解及解空间的 概念,掌握齐次线性方程组的基础解系和通解的求法. ◆8.理解非齐次线性方程组解的结构及通解的概念 ◆9.掌握用初等行变换求解线性方程组的方法
学习考研要求 第三章矩阵的初等变换与线性方程组 1.理解n维向量、向量的线性组合与线性表示的概念. 2.理解向量组线性相关、线性无关的概念,掌握向量 组线性相关、线性无关的有关性质及判别法. 3.理解向量组的极大线性无关组和向量组的秩的概 念,会求向量组的极大线性无关组及秩. 4.理解向量组等价的概念,理解矩阵的秩与其行(列) 向量组的秩之间的关系. 5.了解n维向量空间、子空间、基底、维数、坐标等 概念. 6.了解基变换和坐标变换公式,会求过渡矩阵. 7.理解齐次线性方程组的基础解系、通解及解空间的 概念,掌握齐次线性方程组的基础解系和通解的求法 . 8.理解非齐次线性方程组解的结构及通解的概念. 9.掌握用初等行变换求解线性方程组的方法.

学习内容 第一节向量组及其线性组合 第一节 向量组及其线性组合 1.n维向量 n个数组成的有序数组 A. 称为n维向量,a,称为向量的第i个分量.向 量一般用小写的希腊字母,B,4.表示,分量 一般用小写的英文字母a,b,c,…表示.n维向 量也可以写成行的形式: 0=(a,a2,…,an
学习内容 第一节 向量组及其线性组合 第一节 向量组及其线性组合 n个数组成的有序数组 称为n维向量 , 称为向量的第i个分量 .向 量一般用小写的希腊字母,, …表示,分量 一般用小写的英文字母 , , 表示.n维向 量也可以写成行的形式: ai ai bi ci 1.n维向量 1 2 n a a a 21 ,,, aaa n

学习内容 第一节向量组及其线性组合 特别地,称分量都为0的向量为零向量.记作0 -1 a 称向量 -a= -02 为向量a= 2 的负向量 -an A b 向量相等 设a= 2 B= b2 a, b, 若a=b(6=1,2,…nm) 则称 0与B相等. 记作 a=B
特别地,称分量都为0的向量为零向量 .记作 0 称向量 为向量 的负向量. 1 2 n a a a 向量相等 设 若 则 称 与 相等. ii ba ,2,1 ni 记作 1 2 n a a a 1 2 n a a a 1 2 n b b b 学习内容 第一节 向量组及其线性组合
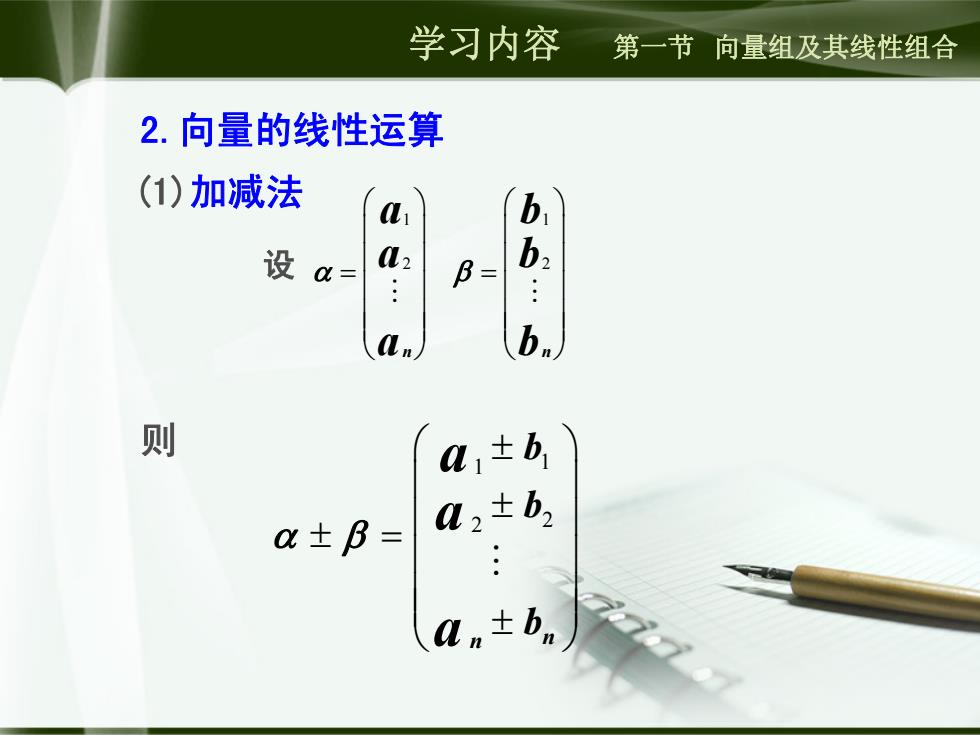
学习内容 第一节向量组及其线性组合 2.向量的线性运算 (1)加减法 b 设 a= A, B= b. 则 a±B= a2±b2 an±bn
2.向量的线性运算 (1)加减法 则 1 2 n a a a 1 2 n b b b 设 1 1 2 2 n n b b b a a a 学习内容 第一节 向量组及其线性组合

学习内容 第一节向量组及其线性组合 a, (2)数乘 设 a= Q, k 为任意实数 k a 则 ka= ka, 运算法则: (1 )a+B=B+a (2) (C+B)+y=a+(B+y) (3)0+0=0 (4) a+(-)=0 (5) (kl)a=k(la)
(2)数乘 设 , k 为任意实数 则 运算法则: (1) (2) )()( (4) (3) 0 )( (5) lkkl )()( 1 2 n a a a 1 2 n k ka ka ka 学习内容 第一节 向量组及其线性组合

学习内容 第一节向量组及其线性组合 (6) 1a=0x (7) (k+Da=ka+la (8) k(a+B)=ka+kB 注意:向量的线性运算法则与矩阵的线性运算 法则没有什么区别
注意:向量的线性运算法则与矩阵的线性运算 法则没有什么区别. (6) (7) (8) 1 )( lklk k )( kk 学习内容 第一节 向量组及其线性组合

学习内容 第一节向量组及其线性组合 3.向量组及其线性组合 若干个同维数的列向量(或同维数的行向 量) 所组成的集合叫做向量组 齐次线性方程组Ax=0的全部解当R(A)<n 时是一个含无限多个n维列向量的向量组
3.向量组及其线性组合 若干个同维数的列向量(或同维数的行向 量) 所组成的集合叫做向量组 齐次线性方程组 的全部解当 时是一个含无限多个 维列向量的向量组. Ax 0 )( nAR n 学习内容 第一节 向量组及其线性组合

学习内容 第一节向量组及其线性组合 向量组与矩阵之间的关系 一方面, m×n矩阵的全体列向量是一个 含有 闭 维列向量的向量组,它的全体行向 量是一个含有 个m维行向量的向量组. 另外, m个n维列向量所组成的向量组A:C1,C2,‘,C心m 构成-个n×m矩阵A=(01,02,…,0Cm) 含有有限个向量的有序向量组与矩阵一对应
一方面, 矩阵的全体列向量是一个 含有 个 维列向量的向量组,它的全体行向 量是一个含有 个 维行向量的向量组. nm n m m n 向量组与矩阵之间的关系 含有有限个向量的有序向量组与矩阵一一对应. 个 维列向量所组成的向量组 : 构成一个 矩阵 m n A m ,,, 21 mn ),,,( A 21 m 另外, 学习内容 第一节 向量组及其线性组合