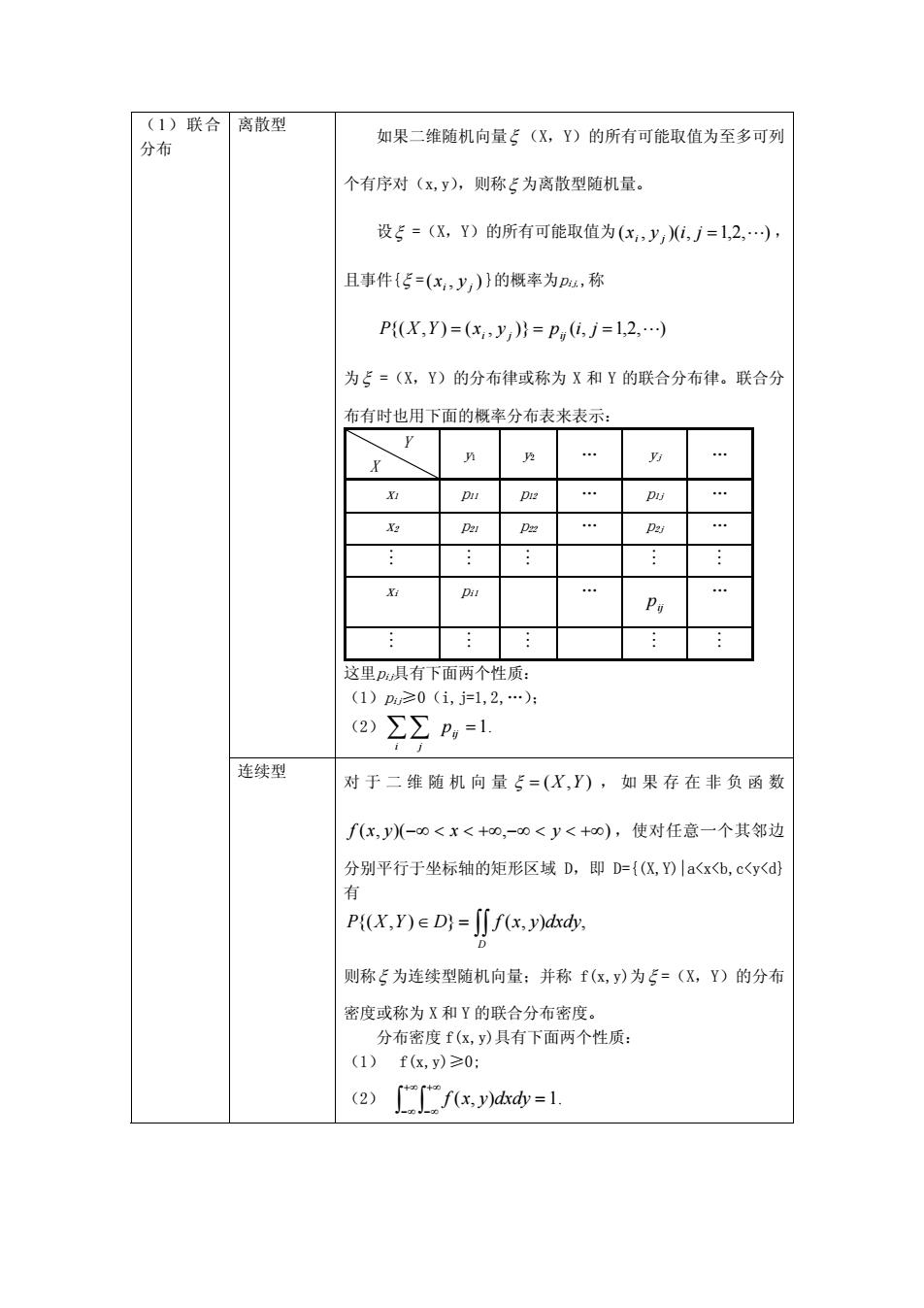
(1)联合离散型 分布 如果二维随机向量:(X,Y)的所有可能取值为至多可列 个有序对(x,y),则称5为离散型随机量 设5=(X,Y)的所有可能取值为(x,y,,j=1,2,), 且事件{5=(x,y,)}的概率为4,称 P{(X,Y)=(xy,)}=p,j=1,2,) 为5=(X,Y)的分布律或称为X和Y的联合分布律。联合分 布有时也用下面的概率分布表来表示: pu p 这里P具有下面两个性质: (1)p≥0(i.j=l.2.…): 2)∑∑P,=1 连续型 对于二维随机向量5=(X,Y),如果存在非负函数 f(x,y)(-0<x<+0,-o<y<+o),使对任意一个其邻边 分别平行于坐标轴的矩形区域D,即D=(仅,)lax,c<y< P{(X,Y)∈Dy=ffx,y)dd 则称5为连续型随机向量:并称f(x,y)为5=(X,Y)的分布 密度或称为X和Y的联合分布密度。 分布密度么,)具有下面两个性质: (1)fk,y)≥0: (2)fxh=1
离散型 如果二维随机向量ξ (X,Y)的所有可能取值为至多可列 个有序对(x,y),则称ξ 为离散型随机量。 设ξ =(X,Y)的所有可能取值为 , 且事件{ jiyx = L),2,1,)(,( ji ξ = ),( }的概率为p ji yx ij,,称 = = jipyxYXP = L),2,1,()},(),{( ji ij 为ξ =(X,Y)的分布律或称为 X 和 Y 的联合分布律。联合分 布有时也用下面的概率分布表来表示: Y X y1 y2 … yj … x1 p11 p12 … p1j … x2 p21 p22 … p2j … M M M M M xi pi1 … pij … M M M M M 这里pij具有下面两个性质: (1)pij≥0(i,j=1,2,…); (2)∑∑ ij = .1 i j p (1)联合 分布 连续型 对于二维随机向量 ξ = YX ),( ,如果存在非负函数 )(,( −∞ < xyxf < +∞,−∞ < y < +∞) ,使对任意一个其邻边 分别平行于坐标轴的矩形区域 D,即 D={(X,Y)|a<x<b,c<y<d} 有 ∫∫ =∈ D dxdyyxfDYXP ,),(}),{( 则称ξ 为连续型随机向量;并称 f(x,y)为ξ =(X,Y)的分布 密度或称为 X 和 Y 的联合分布密度。 分布密度 f(x,y)具有下面两个性质: (1) f(x,y)≥0; (2) ∫ ∫ +∞ ∞− +∞ ∞− dxdyyxf = .1),(

(2)二维 随机变量 E(X=x.Y=y)=5(X=xNY=y) 的本质 (3)联合 设(X,Y)为二维随机变量,对于任意实数x,y,二元函数 分布函数 F(x,y)=PX≤x,Y≤y 称为二维随机向量(X,Y)的分布函数,或称为随机变量X和Y的联合分布函 分布函数是一个以全平面为其定义域,以事件 {(@1,02)川-0x时,有都(x,y)≥F(x,y):当y>y时,有F(亿,y)≥F(x,y): (3)F(x,y)分别对x和y是右连续的,即 F(x.y)=F(x+0.y).F(x.y)=F(x.y+0). (4)F(-0,-D)=F(-m,y)=F(x,-D)=0,F(+0,+o)=1. (5)对于x<x2男1<2 F(x2 y)-F(x2 y)-F(xp 2)+F(x)20 (4)边缘离散型 X的边缘分布为 分布 P.=PX=)=∑P,j=l2 Y的边缘分布为 P,=PY=y,)=∑P0j=12,). 连续型 X的边缘分布密度为 fx(x)=["f(x.y)dy 【的边缘分布密度为 f(y)=[f(x.y)dx. (5)独立 一般型 F(X.Y)=F.(x)F.(y) 离散型 Py PuP. 有零不独立 连续型 f(x.y)=f(x)fr(y)
(2)二维 随机变量 的本质 ξ = == ξ (),( = I = yYxXyYxX ) (3)联合 分布函数 设(X,Y)为二维随机变量,对于任意实数 x,y,二元函数 = ≤ ≤ yYxXPyxF },{),( 称为二维随机向量(X,Y)的分布函数,或称为随机变量 X 和 Y 的联合分布函 数。 分布函数是一个以全平面为其定义域,以事件 })(,)(|),{( 21 1 2 ω ω x1时,有F(x2,y)≥F(x1,y);当y2>y1时,有F(x,y2) ≥F(x,y1); (3)F(x,y)分别对 x 和 y 是右连续的,即 = + = yxFyxFyxFyxF + );0,(),(),,0(),( (4) F −∞=−∞−∞ = −∞ = FxFyF +∞ +∞ = .1),(,0),(),(),( (5)对于 < < yyxx 2121 ,, 0)()()()( , 22 − , 12 − , 21 + ,yxFyxFyxFyxF 11 ≥ . 离散型 X 的边缘分布为 === ∑ = L),2,1,()( • ij jipxXPP j i i ; Y 的边缘分布为 === ∑ = L),2,1,()( • ij jipyYPP i j j 。 (4)边缘 分布 连续型 X 的边缘分布密度为 ∫ +∞ ∞− X = ),()( dyyxfxf ; Y 的边缘分布密度为 .),()( ∫ +∞ ∞− = dxyxfyfY 一般型 F(X,Y)=FX(x)FY(y) 离散型 = ppp •• jiij 有零不独立 (5)独立 性 连续型 f(x,y)=fX(x)fY(y)

维正态分 布 1 月 f(x,y)= 2o,V-p 0=0 随机变量的若X,,…XX,…X相互独立,山g为连续函数,则: 函数 h(X,X,…X)和g(X,…X)相互独立。 特例:若X与Y独立 则:h(X)和g(Y)独立 例如:若X与Y独立,则:3X+1和5Y-2独立。 (6)二维 设随机向量(X,Y)的分布密度函数为 均匀分布 Sp (x,y)ED f(x.y)= 其他 中S为区域D的面积,则称(X,Y)服从D上的均匀分布,记为(X,Y)~U D (7)二维 设随机向量(X,Y)的分布密度函数为 正态分布 1 f(x.y)= 2πo,0,1-p 其中4,42.01>0,02>0,P水1是5个参数,则称(X,Y)服从二维正态分 布 记为(X,Y)~N(4,42o,o,p), 由边缘密度的计算公式,可以推出二维正态分布的两个边缘分布仍为正态分 布, 即X~N(41,o2),Y~N(42σ). 但是若X~N(41,o),Y~N(42.o),(仅,)未必是二维正态分布。 (8)函数Z=X+Y 分布 根据定义计算:Fz(e)=P(Z≤)=P(X+Ys) 对于连续型,=了,:-x达 两个独立的正态分布的和仍为正态分布(4,+山2,0+G) ·个相互独立的正态分布的线性组合,仍服从正态分布。 u=∑C,4,g2-∑Co
, 12 1 ),( 2 2 2 21 21 2 1 1 2 21 ))((2 )1(2 1 2 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + −− − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − − = σ μ σσ μμρ σ μ ρ ρσπσ x yyx yxf e 二维正态分 布 ρ =0 随机变量的 函数 若X1,X2,…Xm,Xm+1,…Xn相互独立, h,g为连续函数,则: h(X1,X2,…Xm)和g(Xm+1,…Xn)相互独立。 特例:若 X 与 Y 独立,则:h(X)和 g(Y)独立。 例如:若 X 与 Y 独立,则:3X+1 和 5Y-2 独立。 (6)二维 均匀分布 设随机向量(X,Y)的分布密度函数为 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ∈ = ,0 其他 ),( 1 ),( Dyx S yxf D 其中SD为区域D的面积,则称(X,Y)服从D上的均匀分布,记为(X,Y)~U (D)。 (7)二维 正态分布 设随机向量(X,Y)的分布密度函数为 , 12 1 ),( 2 2 2 21 21 2 1 1 2 21 ))((2 )1(2 1 2 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + −− − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − − = σ μ σσ μμρ σ μ ρ ρσπσ x yyx yxf e 1||,0,0, 其中 μ μ σ 1,21 σ 2 >> ρ < 是 5 个参数,则称(X,Y)服从二维正态分 布, 记为(X,Y)~N( ).,,, 2 2 2 1,21 ρσσμμ 由边缘密度的计算公式,可以推出二维正态分布的两个边缘分布仍为正态分 布, 即 X~N( ).(~),, 2 2,2 2 σμ 11 NY σμ 但是若 X~N( )(~),, ,(X,Y)未必是二维正态分布。 2 2,2 2 σμ 11 NY σμ (8)函数 分布 Z=X+Y zYXPzZPzF )()()( 根据定义计算: Z = ≤ = + ≤ 对于连续型,fZ(z)= dxxzxf ∫ +∞ ∞− − ),( 两个独立的正态分布的和仍为正态分布( )。2 2 2 121 , ++ σσμμ n 个相互独立的正态分布的线性组合,仍服从正态分布。 = ∑ i C μμ ii , = ∑ i C ii 2 22 σ σ

Z=max.min( XX2.…X) 若X,X2…X。相互独立,其分布函数分别为 F,(xF,(x…F,(x),则Z=max.min(X,X2,…X)的分布丙 数为: F(x)=F(x)·F(x…F(x) E(x)=1-[1-F(x)]-[1-F.(x)]---[1-F (x)] x2分布 设n个随机变量X,X2,…,X。相互独立,且服从标准正态分 布,可以证明它们的平方和 m-2 的分布密度为 1 wg片u≥0 f)= u<0. 我们称随机变量W服从自由度为n的x2分布,记为W~X2(m) 其中 份e 所谓自由度是指独立正态随机变量的个数,它是随机变量 分布中的一个重要参数。 X分布满足可加性:设 y-x2(n,)2
Z=max,min( X 若 相互独立,其分布函数分别为 ,则Z=max,min(X 21 LXXX n , 1,X2,…Xn) )()()( 1 2 xFxFxF n x , x L x 1,X2,…Xn)的分布函 数为: )()()()( max 1 2 xFxFxFxF n x x L x = • )](1[)](1[)](1[1)( min 1 2 xF xFxFxF n x − x − x = − − • L 2 χ 分布 设 n 个随机变量 相互独立,且服从标准正态分 布,可以证明它们的平方和 XXX n ,,, 21 L ∑= = n i XW i 1 2 的分布密度为 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ < ≥ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = Γ −− ,0 .0 ,0 2 2 1 )( 2 1 2 2 u ueu n uf un n 我们称随机变量 W服从自由度为 n的 分布,记为 W~ , 其中 2 χ )( 2 χ n . 2 0 1 2 dxex n x n − ∞+ − ∫ ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ Γ 所谓自由度是指独立正态随机变量的个数,它是随机变量 分布中的一个重要参数。 2 χ 分布满足可加性:设 ),( 2 i − χ nY i 则 (~ ). 21 1 2 k k i = ∑ i +++ nnnYZ = χ L
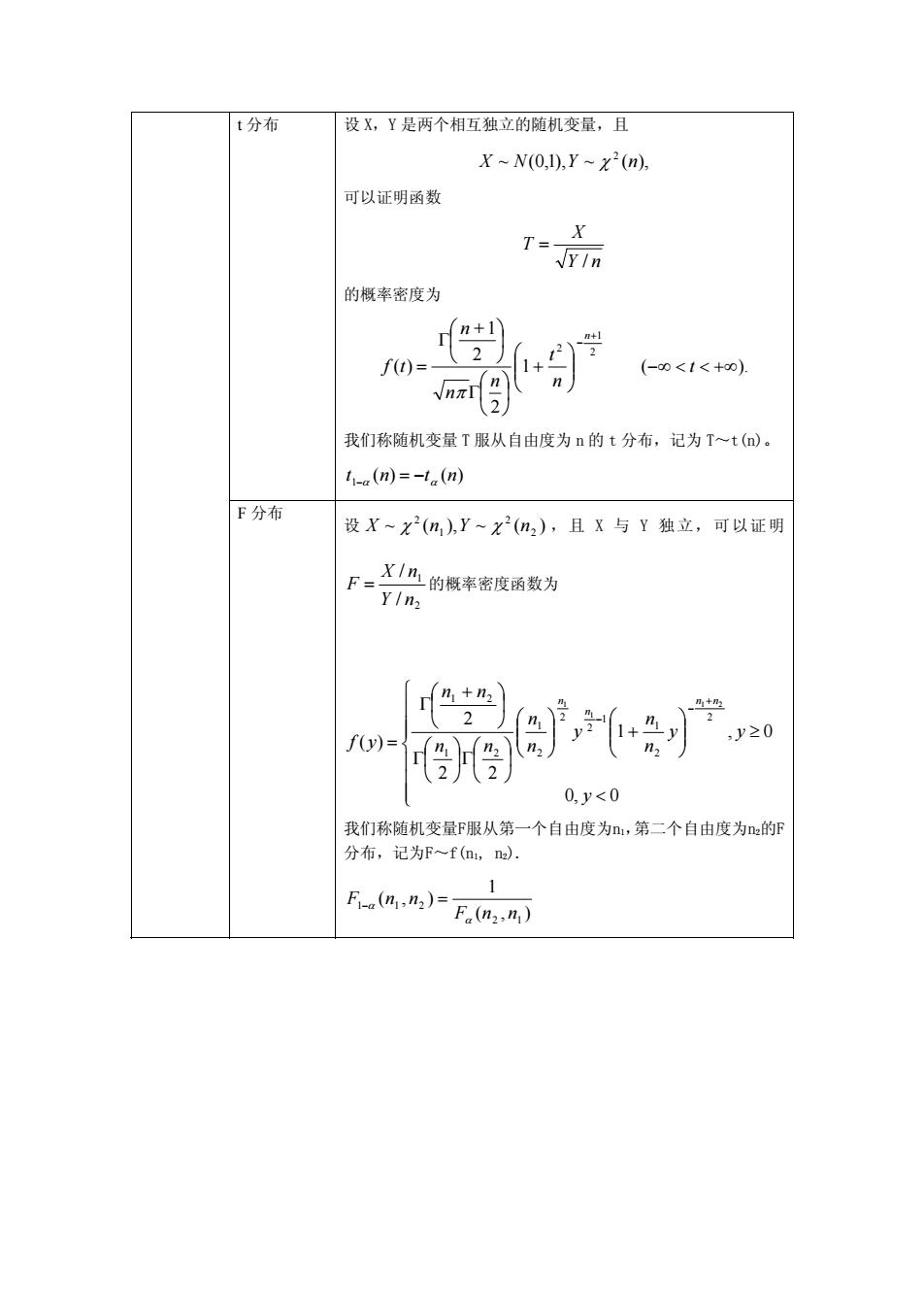
t分布 设X,Y是两个相互独立的随机变量,且 X~N0,1,y-x2(n). 可以证明函数 T=- X 的概率密度为 f()=- 1* n (-0<t<+D) 我们称随机变量T服从自由度为n的t分布,记为T~t() l(m)=-1.(m) F分布 设X~x2(m),Y~x2(n2),且X与Y独立,可以证明 F=X1的概率密度函数为 YIn2 +} f(y)= 0,y<0 我们称随机变最F服从第一个自由度为n,第二个自由度为n:的F 分布,记为F~f(n,n). 1 Fa(n1,n2)= Fa(n2,m)
t 分布 设 X,Y 是两个相互独立的随机变量,且 ),(~),1,0(~ 2 χ nYNX 可以证明函数 nY X T / = 的概率密度为 2 1 2 1 2 2 1 )( + − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + Γ = n n t n n n tf π (−∞ t +∞<< ). 我们称随机变量 T 服从自由度为 n 的 t 分布,记为 T~t(n)。 )()( 1 ntnt −α = − α F 分布 设 2 )(~),(~ ,且 X 与 Y 独立,可以证明 2 1 2 χ χ nYnX 2 1 / / nY nX F = 的概率密度函数为 ⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎨ ⎧ < ≥ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟Γ ⎠ ⎞ ⎜ ⎝ ⎛ Γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + Γ = + − − 0,0 1 0, 22 2 )( 2 2 1 1 2 2 2 1 1 2 21 21 1 1 y yy n n y n n nn nn y nn n n f 我们称随机变量F服从第一个自由度为n1,第二个自由度为n2的F 分布,记为F~f(n1, n2). ),( 1 ),( 12 211 nnF nnF α −α =