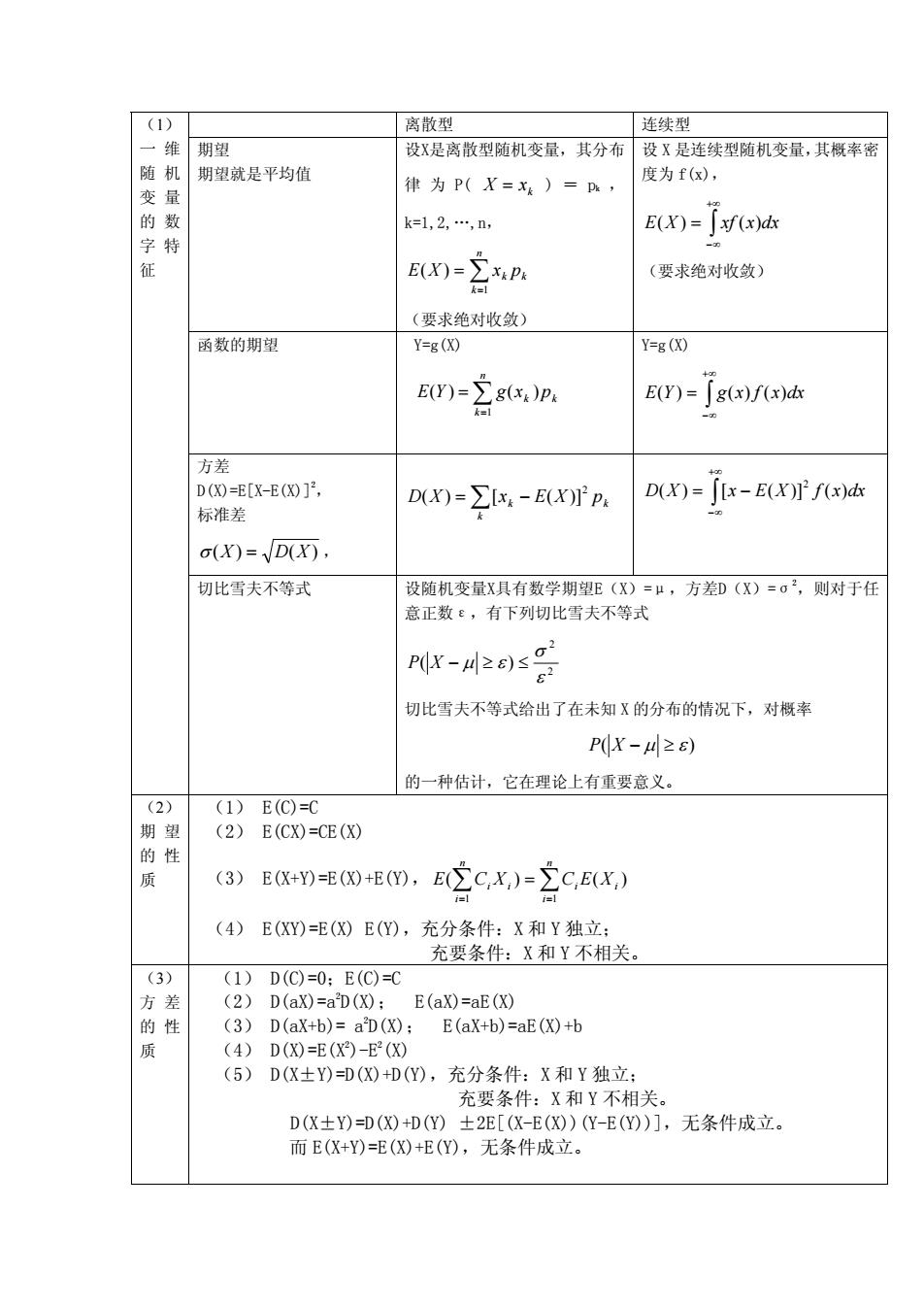
(1) 离散型 连续型 一维期望 设X是离散型随机变最,其分布设X是连续型随机变量,其概率密 期望就是平均值 律为P(X=x)= 度为f(x) k=1,2,…,n, E(X)=「xf(x)d 字特 E(X)-P (要求绝对收敛) (要求绝对收敛) 函数的期望 Y=g(0 Y=g(X) E(Y)=g()p. al EB)=了gx/xh 方差 D(X)=E[X-E(0], 标准差 DX)=∑:-EXIp: D(x)=[[x-E(x)f(x)d (X)=√DX) 切比雪夫不等式 设随机变量X具有数学期望E(X)=μ,方差D(X)=o,则对于任 意正数:,有下列切比雪夫不等式 切比雪夫不等式给出了在未知X的分布的情况下,对概率 P叫X-4≥6) 的一种估计,它在理论上有重要意义。 (1)E(C)=C 期望 (2)E(CX=CE(X 的性 质 (3)E(X+Y)(XE(Y).E(ZCX,)=C,E(X,) (4) E(Y)=E()E(Y),充分条件:X和Y独立 充要条件:X和Y不相关。 (3) (1)D(C)=0:E(C)=C 方差 (2)D(ax)=a'D(X):E(ax)=aE(X) 的性 (3)D(ax+b)=aD(X): E(aX+b)=aE(X)+b (4)D(0=E(X-E(X0 (5)D(X士Y)=D()+D(Y),充分条件:X和Y独立: 充要条件:X和Y不相关。 D(X±Y)=D(X)+D(Y)±2E[(X-E(X))(Y-E(Y)],无条件成立。 而E(X+Y)=E(X)+E(Y),无条件成立
离散型 连续型 期望 期望就是平均值 设X是离散型随机变量,其分布 律 为 P( k = xX )=pk , k=1,2,…,n, ∑= = n k pxXE kk 1 )( (要求绝对收敛) 设 X 是连续型随机变量,其概率密 度为 f(x), ∫ +∞ ∞− = )()( dxxxfXE (要求绝对收敛) (1) 一 维 随 机 变 量 的 数 字 特 征 函数的期望 Y=g(X) Y=g(X) ∫ +∞ ∞− ∑ = )()()( dxxfxgYE = = n k pxgYE kk 1 )()( 方差 ∫ +∞ ∞− −= )()]([)( dxxfXExXD 2 ∑ −= k k pXExXD k 2 )]([)( D(X)=E[X-E(X)]2 , 标准差 σ = XDX )()( , 切比雪夫不等式 设随机变量X具有数学期望E(X)=μ,方差D(X)=σ2 ,则对于任 意正数ε,有下列切比雪夫不等式 2 2 ( ) ε σ XP εμ ≤≥− 切比雪夫不等式给出了在未知 X 的分布的情况下,对概率 XP ≥− εμ )( 的一种估计,它在理论上有重要意义。 (2) 期 望 的 性 质 (1) E(C)=C (2) E(CX)=CE(X) (3) E(X+Y)=E(X)+E(Y), ∑ ∑ = = = n i n i ii XECXCE ii 1 1 )()( (4) E(XY)=E(X) E(Y),充分条件:X 和 Y 独立; 充要条件:X 和 Y 不相关。 (3) 方 差 的 性 质 (1) D(C)=0;E(C)=C (2) D(aX)=a2 D(X); E(aX)=aE(X) (3) D(aX+b)= a2 D(X); E(aX+b)=aE(X)+b (4) D(X)=E(X2 )-E2 (X) (5) D(X±Y)=D(X)+D(Y),充分条件:X 和 Y 独立; 充要条件:X 和 Y 不相关。 D(X±Y)=D(X)+D(Y) ±2E[(X-E(X))(Y-E(Y))],无条件成立。 而 E(X+Y)=E(X)+E(Y),无条件成立
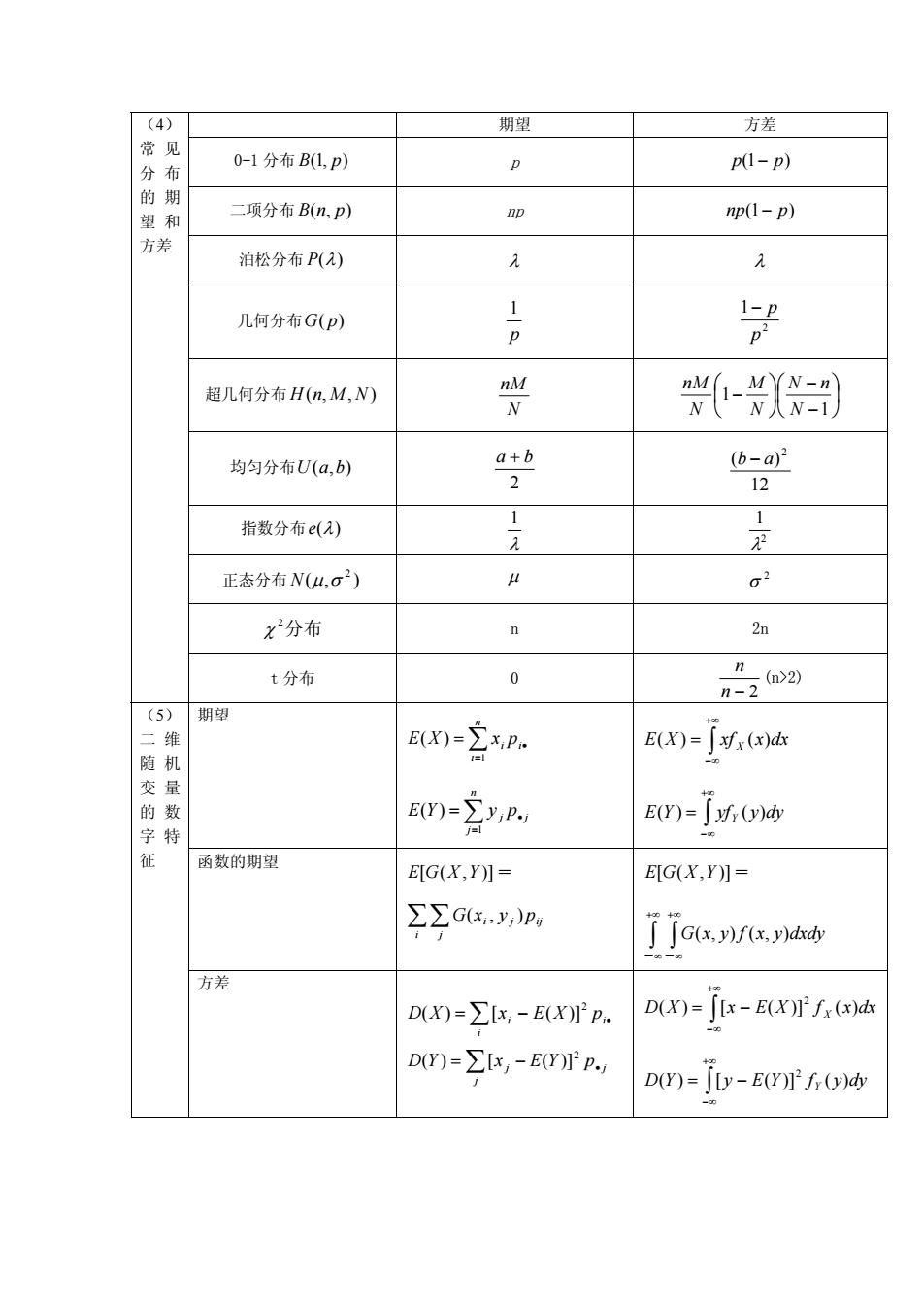
(4) 期望 方差 0-1分布B(1,p) p p(1-p) 望和 二项分布B(n,p) 名 p(1-p) 方 泊松分布P(2) 几何分布G(P) 超几何分布H(n,M,N) 兴 -0别 均匀分布U(a,b) 生 6 指数分布e() 正态分布N(4,o2) 从 x2分布 2n t分布 0 n-2 n2) (5)期望 随机 B0-2P. EX)=了寸xd 变 的数 E()=y,P. E(r)=d 字特 征 函数的期望 EG(X,Y】= ELG(X,Y】 ∑∑Gx,y,p, j ja(x.yf(z.ydd 方差 D(X)=∑x,-E(X)p. D(X)=j[x-E(X∫r(x)d DY)=∑G,-EVIP D(r)=[Ly-E(f(y)dy
期望 方差 0-1 分布 pB ),1( p − pp )1( 二项分布 pnB ),( np − pnp )1( 泊松分布 P λ)( λ λ (4) 常 见 分 布 的 期 望 和 方差 2 1 p − p p 1 几何分布 pG )( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − 1 1 N nN N M N nM N nM 超几何分布 NMnH ),,( 2 + ba 12 )( 2 − ab 均匀分布U ba ),( λ 1 2 1 λ 指数分布e λ)( 正态分布 N σμ 2 ),( μ 2 σ χ2 分布 n 2n n − 2 n t 分布 0 (n>2) 期望 ∑= = • n i pxXE ii 1 )( ∑= = • n j pyYE jj 1 )( ∫ +∞ ∞− = X )()( dxxxfXE ∫ +∞ ∞− = Y )()( dyyyfYE 函数的期望 YXGE )],([ = ∑∑ i j pyxG ijji ),( YXGE )],([ = ∫ ∫ +∞ ∞ +∞ - -∞ ),(),( dxdyyxfyxG (5) 二 维 随 机 变 量 的 数 字 特 征 方差 ∫ +∞ ∞− −= X )()]([)( dxxfXExXD 2 ∑ −= • i i i pXExXD 2 )]([)( ∑ −= • j j pYExYD j 2 )]([)( ∫ +∞ ∞− −= Y )()]([)( dyyfYEyYD 2

协方差 对于随机变量X与Y,称它们的二阶混合中心矩4山,为X与Y的协方 差或相关矩,记为og或cov(X,Y),即 o=41=EX-E(X)Y-E(Y)川 与记号0a相对应。 相关系数 对于随机变量X与Y,如果D(X)>0,D)>0,则称 DX)JDOY) 为X与Y的相关系数,记作Pw(有时可简记为p)。 |p|≤1,当|p|=1时,称X与Y完全相关: P(X=aY+b)=1 完全相关正相关,当p=时a>0, 负相关,当p=-1时(a<0), 而当p=0时,称X与Y不相关。 以下五个命题是等价的: ①pn=0: ②cov(X,Y)=0: ③E(XY)=E(X)E(Y): ④D(X+Y)=D(X)+D(Y) ⑤D(X-Y)=D()+D(Y (6)(i)cov (X,Y)=cov (Y,X) 协方(ii)cov(aX,bY)=ab cov(X,Y): 差的(iii)cov(X+X,Y)=cov(X,Y)+cov(X,Y): 性 w cov(X,Y)=E(XY)-E(X)E(Y). 独立 (i) 若随机变量X与Y相互独立,则p=0:反之不真 和不 相关 (ii) 若(X,Y)~N(4,2,,oi,P), 则X与Y相互独立的充要条件是X和Y不相关
协方差 对于随机变量 X 与 Y,称它们的二阶混合中心矩 μ11为 X 与 Y 的协方 差或相关矩,记为 YX ),cov( σ XY或 ,即 ))].())(([( σ XY = μ11 = − − YEYXEXE 与记号σ XY 相对应。 相关系数 对于随机变量 X 与 Y,如果 D(X)>0, D(Y)>0,则称 YDXD )()( σ XY 为X与Y 的相关系数,记作 ρ XY (有时可简记为 ρ )。 | ρ |≤1,当| ρ |=1 时,称 X 与 Y 完全相关: ( = aY + bXP =1) 完全相关 ⎩ ⎨ ⎧ = 负相关,当 ,时 正相关,当 ,时 )0(1 )0(1 a a ρ ρ 而当 ρ = 0 时,称 X 与 Y 不相关。 以下五个命题是等价的: = 0 ① ρ XY ; ②cov(X,Y)=0; ③E(XY)=E(X)E(Y); ④D(X+Y)=D(X)+D(Y); ⑤D(X-Y)=D(X)+D(Y). (6) (i) cov (X, Y)=cov (Y, X); 协 方 差 的 性质 (ii) cov(aX,bY)=ab cov(X,Y); (iii) cov(X1+X2, Y)=cov(X1,Y)+cov(X2,Y); (iv) cov(X,Y)=E(XY)-E(X)E(Y). (7) 独 立 和 不 相关 = 0 (i) 若随机变量X与Y 相互独立,则 ρ XY ;反之不真。 (ii) 若(X,Y)~N( ,,,, ρσσμμ ), 2 2 2 121 则X与Y 相互独立的充要条件是X和Y 不相关