
第十章定积分的应用 §1平面图形的面积 §2由平行截面面积求体积 §3平面曲线的弧长 §4旋转曲面的面积 §5定积分在物理中的应用
§3 平面曲线的弧长 §4 旋转曲面的面积 §1平面图形的面积 §5 定积分在物理中的应用 §2 由平行截面面积求体积 第十章 定 积 分的应用

§10.1平面图形的面积 一、直角坐标系情形 二、参数方程 三、极坐标情形 四、小结
§10.1平面图形的面积 一、直角坐标系情形 二、参数方程 三、极坐标情形 四、小结
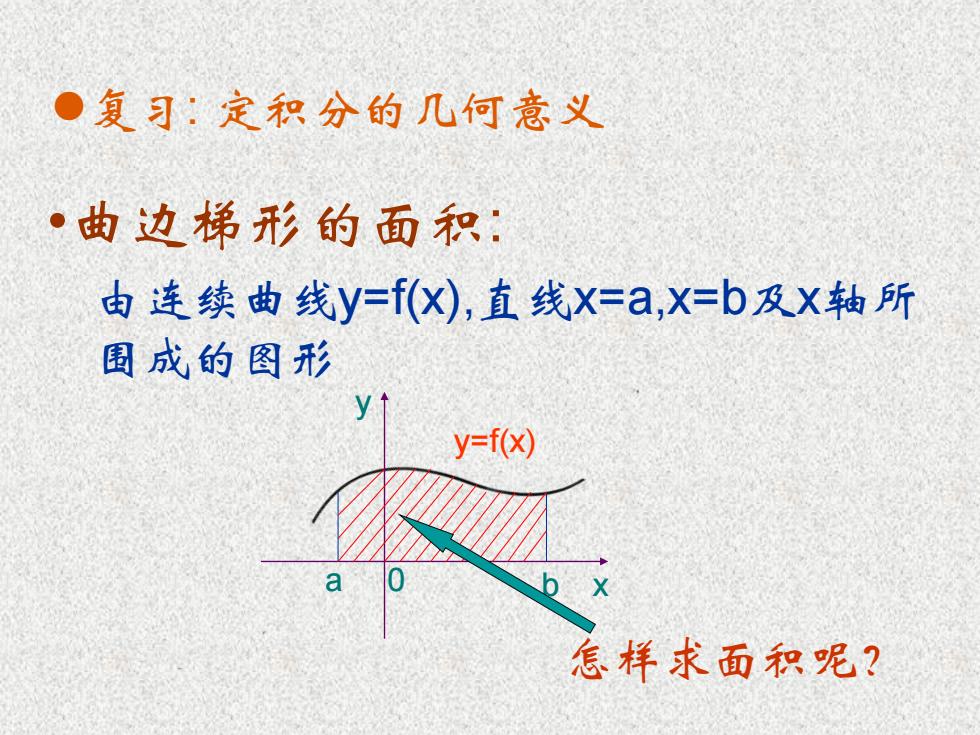
●复习:定积分的几何意义 ·曲边梯形的面积: 由连续曲线y=f((X),直线X=a,X=b及X轴所 围成的图形 y=f(x) 怎样求面积呢?
复习: 定积分的几何意义 •曲边梯形的面积: 由连续曲线y=f(x),直线x=a,x=b及x轴所 围成的图形 y=f(x) a 0 b x y 怎样求面积呢?

-Af(x)0 y↑ y=f(x)<0
f x dx b a 1. ( ) A -A f (x) 0 f (x) 0 A表示以y=f(X)为曲边的曲边梯形面积 a b a b y=f(x)>0 y=f(x)<0 x x y y 0 0 A A
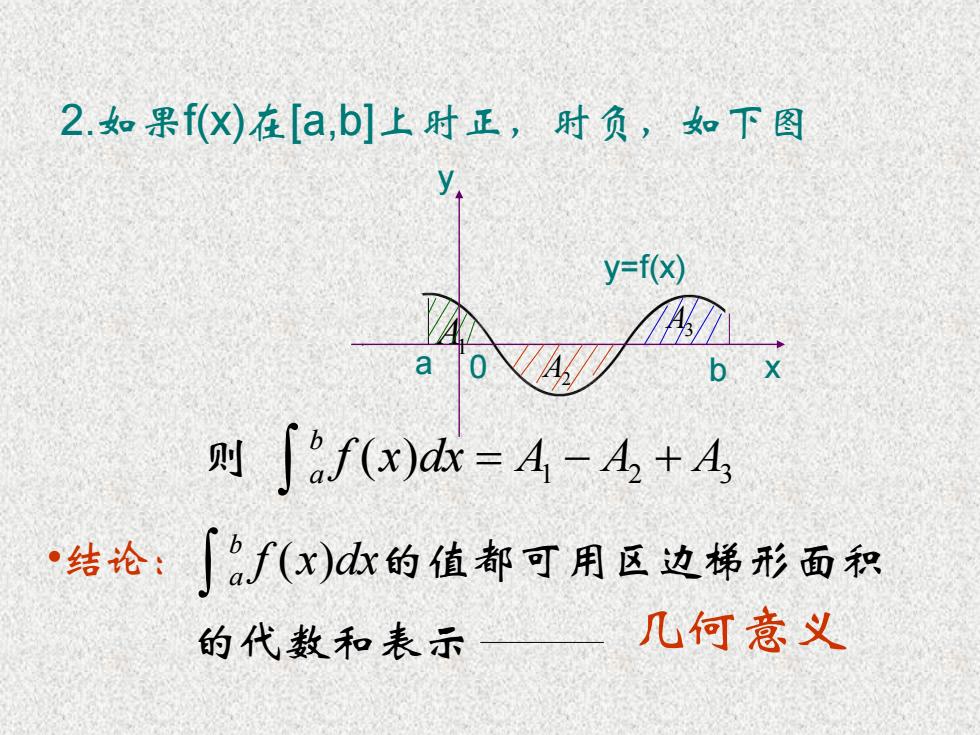
2.如果f()在[a,b]上时正,时负,如下图 y=f(x) b x 则∫f(x)d=A-A+A 结论:∫f(x)的值都可用区边梯形面积 的代数和表示 几何意义
1 2 3 f (x)dx A A A b a 则 2.如果f(x)在[a,b]上时正,时负,如下图 •结论: 的代数和表示 b a f (x)dx的值都可用区边梯形面积 几何意义 a b x y y=f(x) A2 A1 A3 0
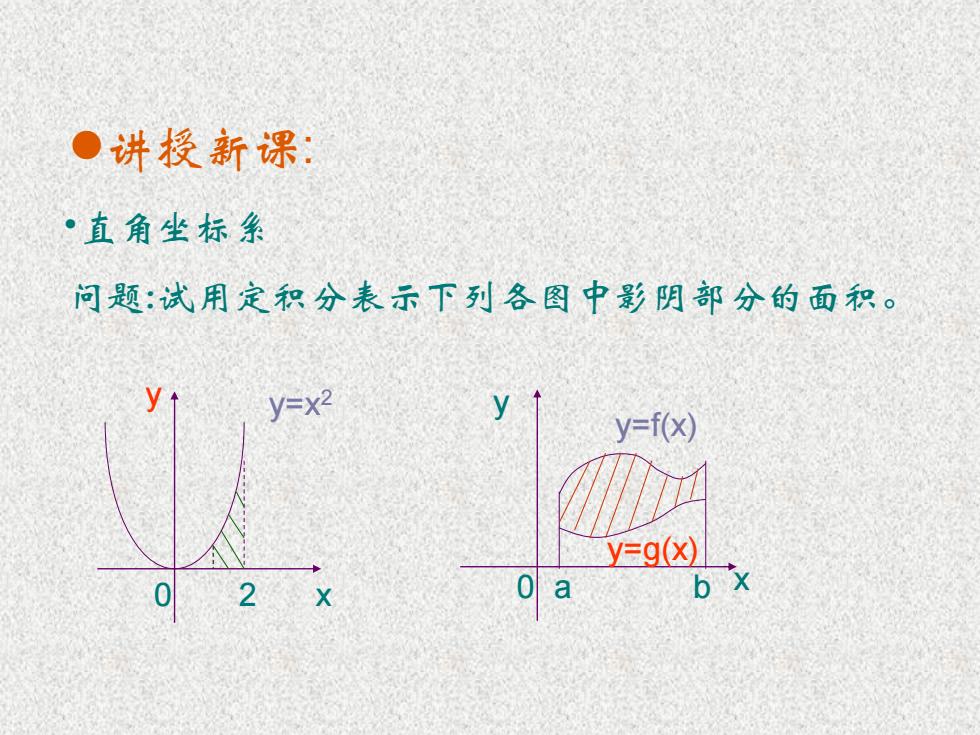
●讲授新课 ·直角坐标系 问题:试用定积分表示下列各图中影阴部分的面积。 y y=x2 y y=f(x) y=g(x) 02 0 a
问题:试用定积分表示下列各图中影阴部分的面积。 0 x y=x2 2 y y 0 x y=f(x) y=g(x) a b 讲授新课: •直角坐标系
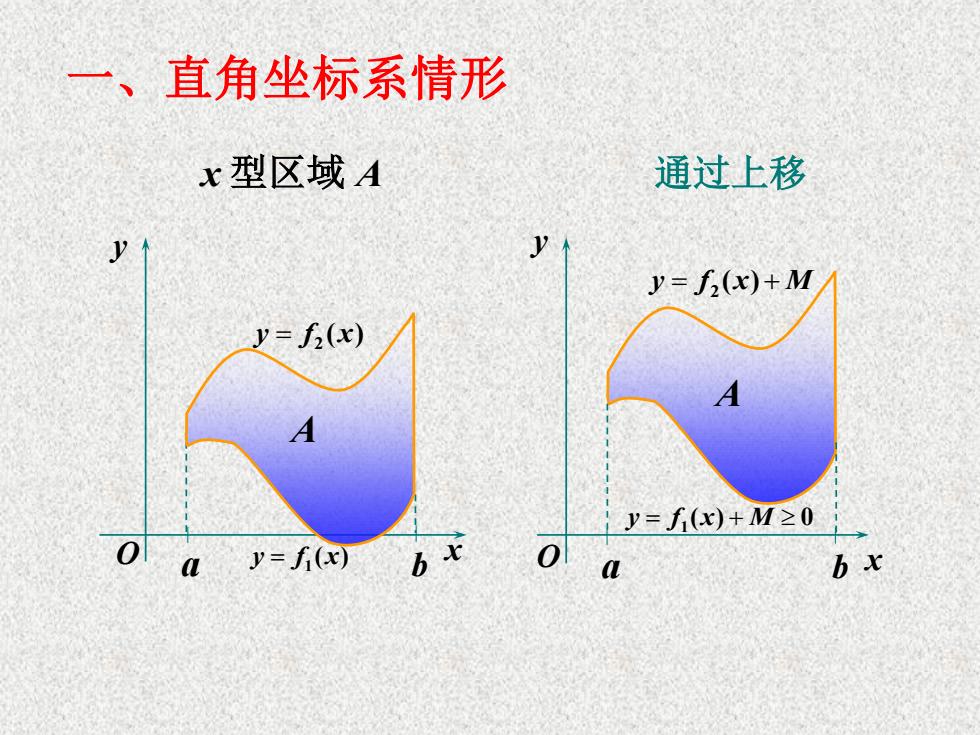
一、直角坐标系情形 x型区域A 通过上移 y=f(x)+M D= f2(x) A y=fi(x)+M≥0 y=f(x) 0 b x
x A 型区域 通过上移 a b x y O 2 y f x ( ) 1 y f x ( ) A x y O a b 2 y f x M ( ) 1 y f x M ( ) 0 A 一、直角坐标系情形

由定积分的几何意义,可知A的面积为 (-(()+M)dx-()+M)dx =∫Lf(x)-fxde. 同理,型区域B的面积为 S(B)=[80)-g10Id. 例1求由抛物线y2=x和x2-8y所围图形A的面积 解 的解为货0售
由定积分的几何意义,可知 A 的面积为 例1 2 2 求由抛物线 y x x y A 和 8 . 所围图形 的面积 解 2 1 2 2 1 2 0 4 , . 8 0 2 y x x x x y y y 的解为 2 1 ( ) ( ( ) )d ( ( ) )d b b a a S A f x M x f x M x 2 1 [ ( ) ( )]d . b a f x f x x 2 1 ( ) [ ( ) ( )]d . d c S B g y g y y 同理,y B 型区域 的面积为

图形A既是x型区域 又是y型区域 9(4,2) V=x 把A看作x型区域,则 x=8y f四号hw)压0 4 于是 c)- 16648 3243
于是 0 4 24 1 3 2 d 8 2 3 3 4 0 2 x x x x S A x . 3 8 24 64 3 16 图形A x 既是 型区域 把 A x 看作 型区域,则 2 4 y x 2 x 8 y 2 (4, 2)x y O A 又是 y型区域. 2 1 2 ( ) , ( ) , 8 x f x f x x

把A看作为y型区域,则g1(y)=y2,82(y)=√8y 于是 ww西)-s子-8 =828_88 33 例2求由y2=x和x-y=2围成的图形A的面积. 解y2=x和x-y=2的交点为(1,-1)和(4,2).图形 A如下图
2 1 2 把 A y g y y g y y 看作为 型区域,则 ( ) , ( ) 8 , 3 3 2 2 2 0 2 2 ( ) 8 d 8 3 3 0 y S A y y y y 于是 . 3 8 3 8 8 3 2 8 例2 2 求由 y x x y A 和 2 . 围成的图形 的面积 解 2 y x x y 和 2 (1, 1) (4,2). 的交点为 和 图形 A 如下图