
一元函数极限、连续(数一)考研真题 6.(09,4分)当x一→0时,fx)=x-sinax与g(r)=x2ln(1-bx)等价无穷小 则() 国a=b=-名@a=Lb=若 一、选择题(将最佳答案的序号域写在括号内) a=-l6=-石D)a=-b= x2 atanx+b1-cos=2,其中d2+2z0,则必有() 1.(94年,3分)设cn1-2x+d0-e 0.4分)极限--+=《) (A1, (B)e. (A)b=4d (B)b=-4d (e-t. (D) (C)a=4c (D)a=-4c 2.(03年,4分)设{a,{.},{6.}均为非负数列,且ima.=0,lm.=1,limc.=oo 二、填空题 则必有() (A)a.<b,对任意n成立.(B)b<cn,对任意n成立 (C)极限1ima.c,不存在(D)极限1imb.c,不存在 2(95年,3分)m1+3x)产= 3.(o4.4分)把x一0时的无穷小a=∫od,B=∫and,7=∫sind'dr 及6年.3分》设m=8,则= 排列起来,使排在后面的是前一个的高阶无穷小,则正确的排列次序是() 3sinx+cos (A)a,37(B)a,x,3(C)3,a,7(D)3,,a 4(97,3分)i0+cosx)ln1+ 4.(07,4分)当x→0时,与VF等价的无穷小量是() 3(9,3分)四中五+-2。 (A)1-e ® (c)+-1 (D)1-cos 5.(08,3分)设函数f(x)在(心+○)内单调有界,{}为数列,下列命题正确的是() 7(03.4分)m(cos= ()若{红.}收敛,则{f收敛B)若{}单调,则{/区.}收敛 &(,4分)回 (C若{f八(x)}收敛,则{x,}收敛D)若{f红)}单调,则{x}收敛 第1页共2页
一元函数极限、连续(数一)考研真题 第 页 共 页 一、选择题(将最佳答案的序号填写在括号内) 1. (94 年,3 分)设 2 (1 cos ) 2 ) ) x x a xb x c x + - = - + 2 2 a c + ¹ 0 b = 4 b d = -4 a = 4 a c = -4 { }{ } , , n n a b 0, lim 1 n n a b ¥ = = 对任意 , n n bc n < 对任意 成立. lim n n a c ¥ lim n n b c ¥ x 0 tan lim ln(1 2 d e (1 - - ,其中 ,则必有( ) (A) d (B) (C) c (D) 2. (03 年,4 分)设 n 均为非负数列,且 则必有( ) { } c limn n ¥ , lim , n n c ¥ = ¥ (A) a b n n < , n成立. (B) (C)极限 n 不存在 (D)极限 n 不存在 3. (04,4 分) 把 时的无穷小 0 + 2 tan , x tdt g 2 3 0 0 cos , x x a b = = t dt 0 = sin t dt ò ò ò a b , , b a, ,g b g, ,a 0+ 排列起来,使排在后面的是前一个的高阶无穷小,则正确的排列次序是( ) (A) , ,g (B) ( a g b C) (D) 4. (07,4 分)当 时,与 x x 等价的无穷小量是( ) (A)1 x -e (B) 1 ln 1 x x + - (C) 1 1 + -x (D)1 cos - x 5. (08,3 分)设函数 f ( ) x 在( , - + ¥ ¥)内单调有界,{ }n x 为数列,下列命题正确的是( ) (A) { } (B) n n 若 收敛,则 x { } f ( ) x 收敛 若{} { ( ) n n x f 单调,则 x { } {} ( ) n n f x 单调,则 收敛 x x 0 f ( ) sin }收敛 (C) { } ( ) (D) n n 若 收敛,则 f x { } x 收敛 若 6. (09,4 分)当 时, xx a = - 2 x 与 g x x bx ( ) ln(1 ) = - 等价无穷小, 则( ) (A) 1 1, 6 a b = =- (B) 1 1, 6 a b = = (C) 1 1, 6 a b =- =- (D) 1 1, 6 a b =- = 7. (10,4 分)极限 2 lim ( )( ) n n x ¥ x ax b æ ö ç ÷ ç ÷÷ = çç - + ÷ è ø 1 e a b e - b a e - ( ) (A) . (B) . (C) . (D) 二、填空题 1.(94 年,3 分) 0 1 1 lim cot x sin x x x æ ö ç - ÷ ç ÷ ç ÷ è ø= 2.(95 年,3 分) 2 sin 0 lim(1 3 ) x x x + = 3.(96 年,3 分)设 2 lim( ) 8 x x x a ¥ x a + = - ,则 a = 2 0 1 3sin cos lim (1 cos )ln(1 ) x x x x 4.(97,3 分) x x + = + + . 2 0 1 12 lim x x x x ++ -- 5.(98,3 分) = . 6. (99,3 分) 2 0 1 1 limx x x x tan æ ö ç - =÷ ç ÷ ç ÷ è ø . 2 1 ln(1 ) 0 lim(cos ) x x x + 7. (03,4 分) = 8. (06,4 分) 0 ln(1 ) lim 1 cos x x x x + = - 1 2
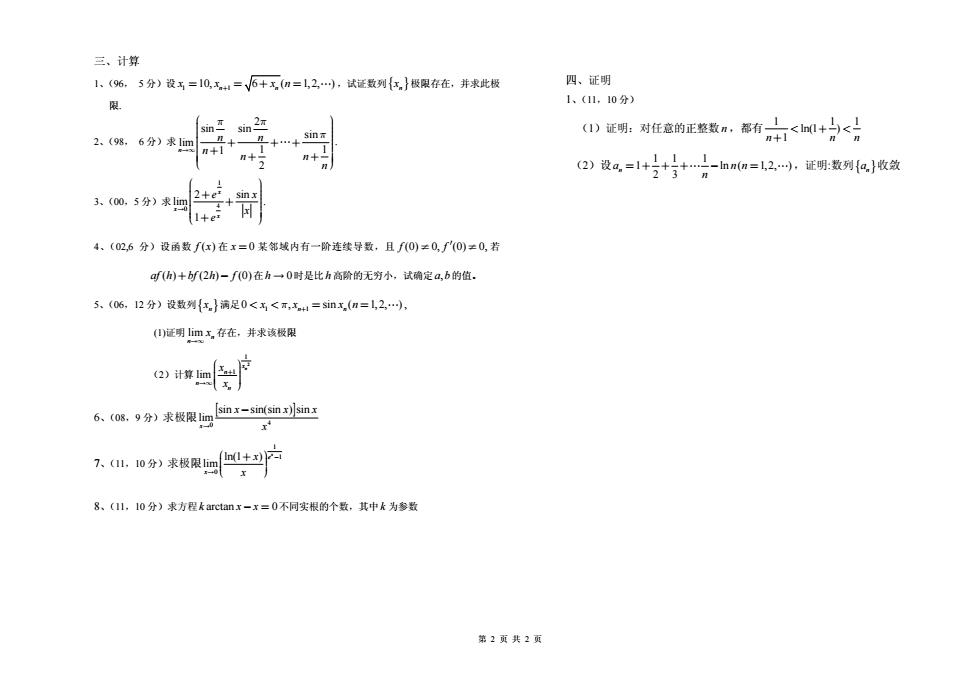
三、计算 1、(96,5分)设=10,x4=V6+x(m=L,2,),试适数列{x}极限存在,并求此极 四、证明 限 1、(11,10分) sin 2.(98,6分)求1m )证明.对任意的正整数a,常有中<+中< n+1 a)设a=1+片计】naa=2小,E明数e)收效 3、(00,5分)求im sinx 4、(02,6分)设函数f(x)在x=0某邻域内有一阶连续导数,且f0)≠0f'(0)≠0,若 a(h)+bf(2h)-f(O)在h→0时是比h高阶的无穷小,试确定a,b的值. 5.(06,12分)设数列{x}满足0<无<T,x=sinx,(n=12,), ()证明1imx,存在,并求该极限 6、(o.9分)求极限回如- 入0》来授限回户 8、(1l,10分)求方程karctan.x-x=0不同实根的个数,其中k为参数 第2页共2页
(1)证明:对任意的正整数 ,都有 n 1 11 ln(1 ) n nn 1 < +< + 第 2 页 共 2 页 (2)设 11 1 1 ln (n 1, 2, ),证明:数列 收敛 2 3 n a n n =+ + + - = { }n a 1、(11,10 分) 四、证明 4、(02,6 分)设函数 f ( ) x f (2 ) h 在 某邻域内有一阶连续导数,且 若 在 时是比 高阶的无穷小,试确定 的值。 x = 0 f (0) f f (0) 0, (0) 0, ¹ ¹ ¢ af ( ) h b + - h 0 h a b, 1、(96, 5 分)设 1 1 10, 6 ( 1,2, ) n n x x xn = =+ = + ,试证数列{ }n x 极限存在,并求此极 限. 2、(98, 6 分)求 2 sin sin sin lim 1 1 1 2 n n n n n n n p p p ¥ æ ö ç ÷ ç ÷ ç ÷÷ ç + ++ ÷ ç ÷ ç + ÷ ç + + ÷ çç ÷÷ è ø . 5、(06,12 分)设数列{ }n x 满足 , 1 1 0 , sin ( 1,2, ) n n << = = x x xn p + 三、计算 3、(00,5 分)求 1 4 0 2 sin lim 1 x x x e x x e æ ö ç ÷ ç + ÷ ç + ÷÷ ç ÷ ç ÷ çç + ÷÷ è ø. (1)证明 lim n n x ¥ 存在,并求该极限 (2)计算 2 1 1 lim nx n n n x x + ¥ æ ö ç ÷ ç ÷ ç ÷ ç ÷ è ø 6、(08,9 分)求极限 [ ] 4 0 sin sin(sin ) sin limx x x x x - 7、(11,10 分)求极限 1 1 0 ln(1 ) lim x e x x x - æ ö ç + ÷ ç ÷ ç ÷ è ø 8、(11,10 分)求方程 k xx arctan 0 - = 不同实根的个数,其中 为参数 k