
REFERENCE page 1 ALGEBRA GEOMETRY Arithmetic Operations Geometric Formulas a(b+c)-ab ac Formulas for area A.circumference C.and volume V: Sector of Circle -+ b -- A-ar A=支r0 -ab sin C=2mr s =re (0 in radians) Exponents and Radicals (r"=x (xyr=x'y (- Sphere Cylinder Cone x-严-( V-far V-r汤 V-rh - A -4mri A-TP+ Factoring Special Polynomials x-y-+y-y) 'y=+y-xy+y) x3-y2-x-yx2++y Binomial Theorem Distance and Midpoint Formulas (x+y=x2+2xy+y x-=x2-2y+y2 Distance between P(y)and P(): x++3xy +3ry2+y' (x-y3=x3-3x2y+3ry2-y3 f(色,”2) ++(y+ …+y1+y (日-a-a-k+ Lines 1…2…3……k Slope of line through P(y)and P:(x2.y) Quadratic Formula 亚am2+c+e-0.henr--b±y- 2a Point-slope equation of line through P)with slopem Inequalities and Absolute Value y-为=m-) If a0.then ca cb. y=mx +b If a b and c0.then Circles x-a means x-a or x-- Equation of the circle with center (h,k)and radius r xa means >a or r<- (x-+(y--2
REFERENCE page 1 Cut here and keep for reference GEOMETRY Geometric Formulas Formulas for area A, circumference C, and volume V: Triangle Circle Sector of Circle A − 1 2 bh A − r 2 A − 1 2 r 2 − 1 2 ab sin C − 2 r s − r s in radiansd r r r s ¨ ¨ a h b Sphere Cylinder Cone V − 4 3 r 3 V − r 2 h V − 1 3 r 2 h A − 4 r 2 A − rsr 2 1 h2 U r U K K Distance and Midpoint Formulas Distance between P1sx1, y1d and P2sx2, y2d: d − ssx2 2 x1d2 1 s y2 2 y1d2 Midpoint of P1P2: S x1 1 x2 2 , y1 1 y2 2 D Lines Slope of line through P1sx1, y1d and P2sx2, y2d: m − y2 2 y1 x2 2 x1 Point-slope equation of line through P1sx1, y1d with slope m: y 2 y1 − msx 2 x1d Slope-intercept equation of line with slope m and y-intercept b: y − mx 1 b Circles Equation of the circle with center sh, kd and radius r: sx 2 hd 2 1 s y 2 kd 2 − r 2 ALGEBRA Arithmetic Operations asb 1 cd − ab 1 ac a b 1 c d − ad 1 bc bd a 1 c b − a b 1 c b a b c d − a b 3 d c − ad bc Exponents and Radicals x mx n − x m1n x m x n − x m2n sx md n − x mn x2n − 1 x n sxyd n − x n yn S x y D n − x n yn x 1yn − s n x x myn − s n x m − (s n x ) m s n xy − s n x s n y În x y − s n x s n y Factoring Special Polynomials x 2 2 y2 − sx 1 ydsx 2 yd x 3 1 y3 − sx 1 ydsx 2 2 xy 1 y2 d x 3 2 y3 − sx 2 ydsx 2 1 xy 1 y2 d Binomial Theorem sx 1 yd 2 − x 2 1 2xy 1 y2 sx 2 yd 2 − x 2 2 2xy 1 y2 sx 1 yd 3 − x 3 1 3x 2 y 1 3xy2 1 y3 sx 2 yd 3 − x 3 2 3x 2 y 1 3xy2 2 y3 sx 1 yd n − x n 1 nx n21 y 1 nsn 2 1d 2 x n22 y2 1 … 1 S n kDx n2k yk 1 … 1 nxyn21 1 yn where S n kD − nsn 2 1d … sn 2 k 1 1d 1 ? 2 ? 3 ? … ? k Quadratic Formula If ax 2 1 bx 1 c − 0, then x − 2b 6 sb 2 2 4ac 2a . Inequalities and Absolute Value If a , b and b , c, then a , c. If a , b, then a 1 c , b 1 c. If a , b and c . 0, then ca , cb. If a , b and c , 0, then ca . cb. If a . 0, then | x | − a means x − a or x − 2a | x | , a means 2a , x , a | x | . a means x . a or x , 2a Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it
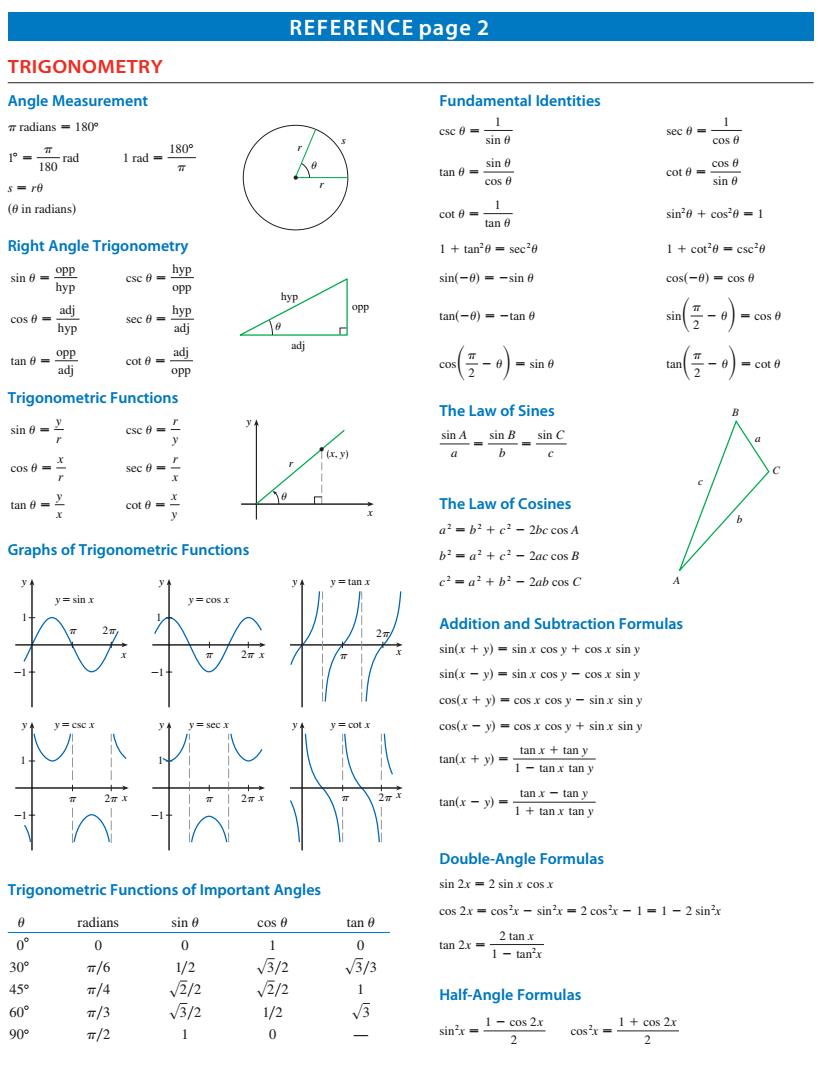
REFERENCE page 2 TRIGONOMETRY Angle Measurement Fundamental Identitie T radians-18 1 rad ,1809 s=0 m0-8 (0in radians) cot tan 0 sin+cos Right Angle Trigonometry 1+tan'0-scc0 1+cot0=csc0 csc o-hyp opp sin(-0)=-sin cos(-8)=cos8 tan(-0)=-tan 8 m号-0)-m0 m0- co5-0)=sng tan(-)-co.o Trigonometric Functions The Law of Sines in csc sinA sin B sin C sec an 6= The Law of Cosines +e2-2bc cosA b2=a+e2-2ac cos B a+b-2ab cos C Addition and Subtraction Formulas sin(x +y)=sin x cos y cosx sin y in(r-y)=sinx cosy -cosx siny cosx+y)=cosx cosy sinx sin y 国 cos(x-y)=cos x cos y sinx sin y an(r+y)= tanx tan y 1 tanx tan y Double-Angle Formulas Trigonometric Functions of Important Angles sin 2x =2 sin x cosx cos 2x =cos-sinx=2 cos-1=1-2sin radians sin 6 cos 8 tan 6 tan 2x 1-tan'x 2 tan x 0 6 /2 5/2 v3/3 45 /4 √2/2 2/2 Half-Angle Formulas 60 5/2 1/2 90° π/2 0 -cos 2x cos+cos 2x 2
TRIGONOMETRY REFERENCE page 2 Fundamental Identities csc − 1 sin sec − 1 cos tan − sin cos cot − cos sin cot − 1 tan sin2 1 cos2 − 1 1 1 tan2 − sec2 1 1 cot2 − csc2 sins2 d − 2sin coss2 d − cos tans2 d − 2tan sinS 2 2 D − cos cosS 2 2 D − sin tanS 2 2 D − cot The Law of Sines sin A a − sin B b − sin C c A b c a B C The Law of Cosines a 2 − b 2 1 c 2 2 2bc cos A b 2 − a 2 1 c 2 2 2ac cos B c 2 − a 2 1 b 2 2 2ab cos C Addition and Subtraction Formulas sinsx 1 yd − sin x cos y 1 cos x sin y sinsx 2 yd − sin x cos y 2 cos x sin y cossx 1 yd − cos x cos y 2 sin x sin y cossx 2 yd − cos x cos y 1 sin x sin y tansx 1 yd − tan x 1 tan y 1 2 tan x tan y tansx 2 yd − tan x 2 tan y 1 1 tan x tan y Double-Angle Formulas sin 2x − 2 sin x cos x cos 2x − cos2 x 2 sin2 x − 2 cos2 x 2 1 − 1 2 2 sin2 x tan 2x − 2 tan x 1 2 tan2 x Half-Angle Formulas sin2 x − 1 2 cos 2x 2 cos2 x − 1 1 cos 2x 2 Angle Measurement radians − 1808 r r ¨ s 18 − 180 rad 1 rad − 180° s − r s in radiansd Right Angle Trigonometry sin − opp hyp csc − hyp opp ¨ opp adj hyp cos − adj hyp sec − hyp adj tan − opp adj cot − adj opp Trigonometric Functions sin − y r csc − r y (x, y) r ¨ x y cos − x r sec − r x tan − y x cot − x y Graphs of Trigonometric Functions π 2π x y y=cot x x 1 _1 y π 2π y=csc x y=sec x π 2π x y 1 _1 x y π 2π y=tan x y=cos x π 2π x y 1 _1 y=sin x x y 1 _1 π 2π Trigonometric Functions of Important Angles radians sin cos tan 08 0 0 1 0 308 y6 1y2 s3y2 s3y3 458 y4 s2y2 s2y2 1 608 y3 s3y2 1y2 s3 908 y2 1 0 — Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it
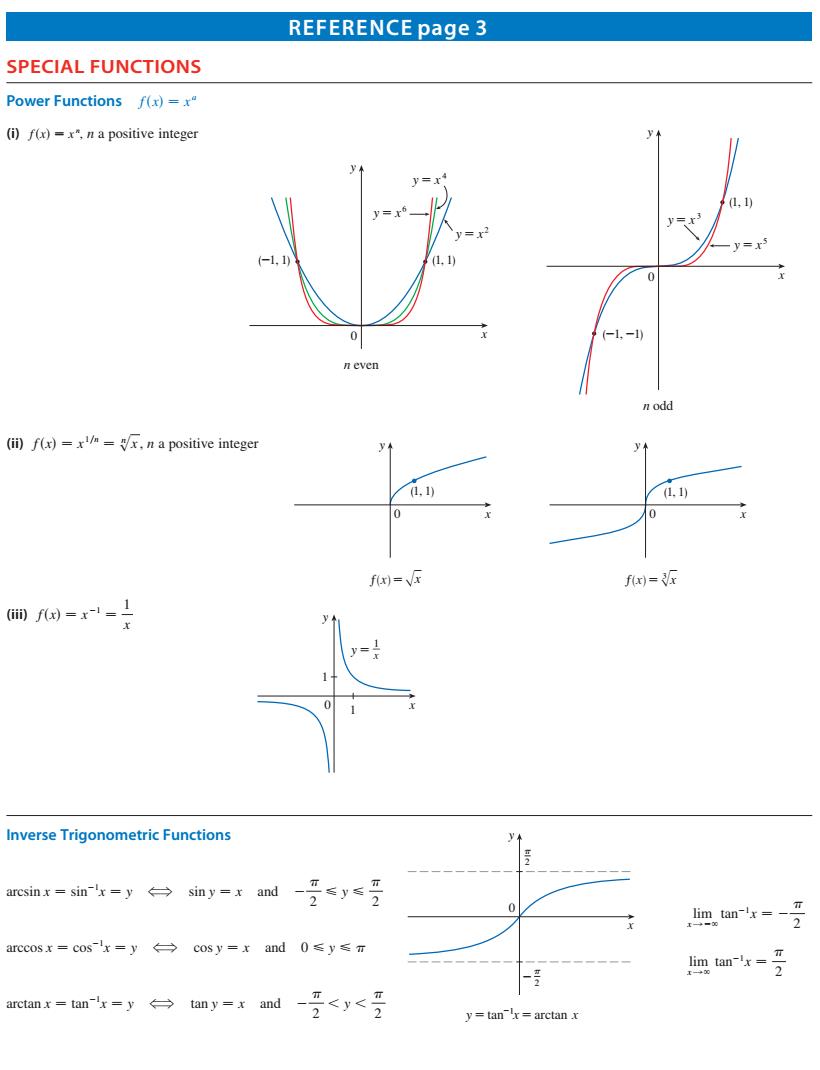
REFERENCE page 3 SPECIAL FUNCTIONS Power Functions f(x)-=x" (i)fr)x"napositive integer (ii)f(r)napositive integer f=派 nverse Trigonometric Functions arcsinx-sin-'x-y→ siny=xand-号≤y≤ m-号 arccosx=cos-x=y←→cosy=xand0≤y≤m mmx=m-y台my--号<y<号 y=tan-r=arctan x
REFERENCE page 3 Cut here and keep for reference SPECIAL FUNCTIONS Power Functions f sxd − x a (i) fsxd − x n , n a positive integer x y 0 y=x# y=x% (_1, _1) (1, 1) n odd n even 0 y x y=x$ (_1, 1) (1, 1) y=x^ y=≈ (ii) fsxd − x 1yn − s n x , n a positive integer ƒ=œ„x ƒ=#œ„x x y 0 (1, 1) x y 0 (1, 1) (iii) fsxd − x 21 − 1 x x 1 y 1 0 y=∆ Inverse Trigonometric Functions arcsin x − sin21 x − y &? sin y − x and 2 2 < y < 2 arccos x − cos21 x − y &? cos y − x and 0 < y < arctan x − tan21 x − y &? tan y − x and 2 2 , y , 2 y=tan–!x=arctan x π 2 _ π 2 y 0 x lim xl2` tan21 x − 2 2 lim xl` tan21 x − 2 Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it
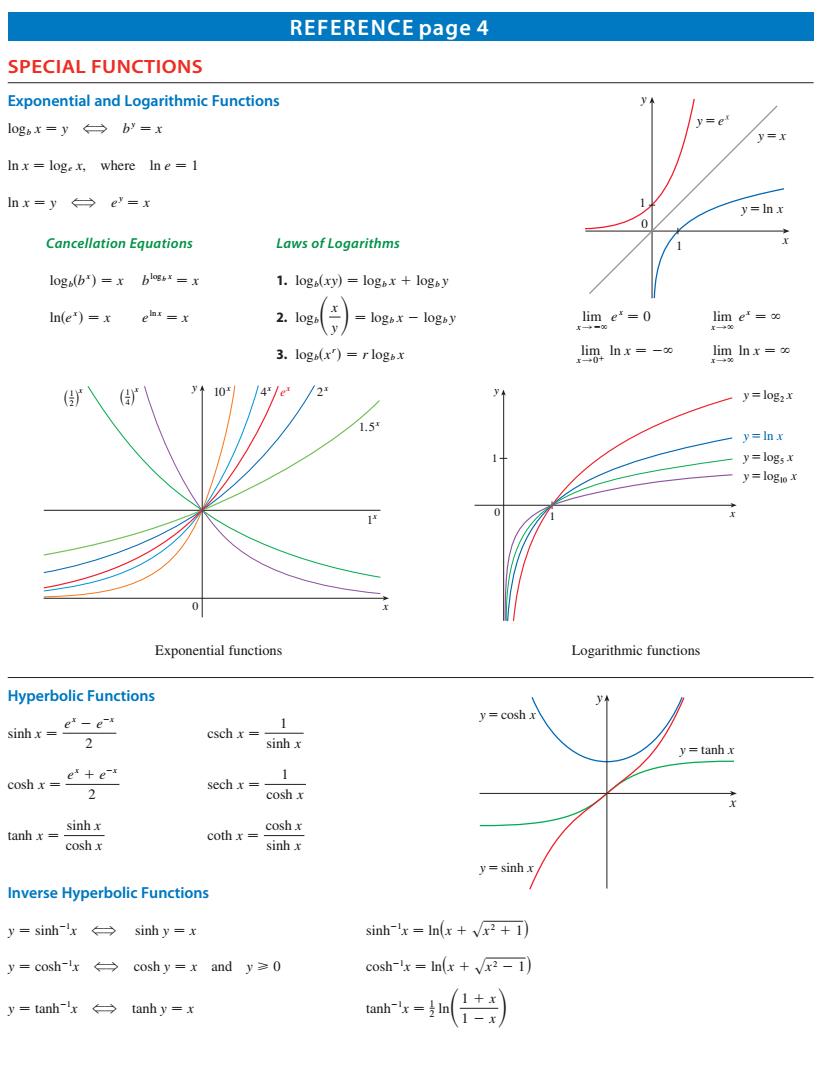
REFERENCE page 4 SPECIAL FUNCTIONS Exponential and Logarithmic Functions ogbx=y→b'=x =e Inx log,x.where In e=1 nx-y→e'-x =hx Cancellation Equations Laws of Logarithms logs(b")-x bl=x 1.loga(xy)=logox logsy In(e")=x =x 2e(月)-gr-y lim e=0 lim e'-o 3.log(x)=rlogs limg,Inx =-%0 lim Inx=x /2 y=log,x 15 0号5 Exponential functions Logarithmic functions Hyperbolic Functions sinhx=e'e y=cosh csch-sint天 tanh 1 2 tanhx=sinhx cosh r ohm y=sinh nverse Hyperbolic Functions y=sinhx→sinhy=x sinh 'x In(x+1) y=cosh-1x→coshy=x and y≥0 cosh-lx -In(x+) y=tanh'x←→tanhy=x b)
REFERENCE page 4 Exponential and Logarithmic Functions y 1 0 x 1 y=x y=´ y=ln x logb x − y &? by − x ln x − loge x, where ln e − 1 ln x − y &? ey − x Cancellation Equations Laws of Logarithms logbsbx d − x blogb x − x 1. logbsxyd − logb x 1 logb y lnsex d − x eln x − x 2. logbS x y D − logb x 2 logb y 3. logbsxr d − r logb x 4® e® 0 1® 1.5® 10® 2® ” ’ 1 ® 4 ” ’ 1 ® 2 x y 0 y 1 x 1 y=ln x y=log™ x y=log∞ x y=log¡¸ x Exponential functions Logarithmic functions Hyperbolic Functions y x y=sinh x y=cosh x y=tanh x sinh x − ex 2 e2x 2 csch x − 1 sinh x cosh x − ex 1 e2x 2 sech x − 1 cosh x tanh x − sinh x cosh x coth x − cosh x sinh x Inverse Hyperbolic Functions y − sinh21 x &? sinh y − x sinh21 x − lnsx 1 sx 2 1 1d y − cosh21 x &? cosh y − x and y > 0 cosh21 x − lnsx 1 sx 2 2 1d y − tanh21 x &? tanh y − x tanh21 x − 1 2 lnS 1 1 x 1 2 x D lim xl2` ex − 0 lim xl` ex − ` lim xl01 ln x − 2` lim xl` ln x − ` SPECIAL FUNCTIONS Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it

REFERENCE page 5 DIFFERENTIATION RULES General Formulas 2&e-f网 3盖+=r四+a 4&/a-创=f-g s.)(Pobe Rde) 6盖[]-r四 Io(x)P (Quotient Rule) Exponential and Logarithmic Functions . 10去)-brnb n会l- 2去e-b Trigonometric Functions 13. 15会m= 16名c动=-ocmr 会@e司=国 18.六ea=-cc Inverse Trigonometric Functions 1 1 1 1-x 20(e为=- 21.am=1+ 22 28c=W 1 Hyperbolic Functions 25去h司-o 6去ah用 2动=的 28. Inverse Hyperbolic Functions 3孔去a分- 1 1 1 1+x 32会eo'划- 2-i 3.会ah-1-子 34 d 1 1 1 35. d 36
Cut here and keep for reference DIFFERENTIATION RULES REFERENCE page 5 General Formulas 1. d dx scd − 0 2. d dx fcfsxdg − cf9sxd 3. d dx f fsxd 1 tsxdg − f9sxd 1 t9sxd 4. d dx f fsxd 2 tsxdg − f9sxd 2 t9sxd 5. d dx f fsxd tsxdg − fsxd t9sxd 1 tsxd f9sxd (Product Rule) 6. d dx F fsxd tsxd G − tsxd f9sxd 2 fsxd t9sxd f tsxdg2 (Quotient Rule) 7. d dx fs tsxdd − f9s tsxdd t9sxd (Chain Rule) 8. d dx sx n d − nx n21 (Power Rule) Exponential and Logarithmic Functions 9. d dx sex d − ex 10. d dx sbx d − bx ln b 11. d dx ln | x | − 1 x 12. d dx slogb xd − 1 x ln b Trigonometric Functions 13. d dx ssin xd − cos x 14. d dx scos xd − 2sin x 15. d dx stan xd − sec2 x 16. d dx scsc xd − 2csc x cot x 17. d dx ssec xd − sec x tan x 18. d dx scot xd − 2csc2 x Inverse Trigonometric Functions 19. d dx ssin21 xd − 1 s1 2 x 2 20. d dx scos21 xd − 2 1 s1 2 x 2 21. d dx stan21 xd − 1 1 1 x 2 22. d dx scsc21 xd − 2 1 xsx 2 2 1 23. d dx ssec21 xd − 1 xsx 2 2 1 24. d dx scot21 xd − 2 1 1 1 x 2 Hyperbolic Functions 25. d dx ssinh xd − cosh x 26. d dx scosh xd − sinh x 27. d dx stanh xd − sech2 x 28. d dx scsch xd − 2csch x coth x 29. d dx ssech xd − 2sech x tanh x 30. d dx scoth xd − 2csch2 x Inverse Hyperbolic Functions 31. d dx ssinh21 xd − 1 s1 1 x 2 32. d dx scosh21 xd − 1 sx 2 2 1 33. d dx stanh21 xd − 1 1 2 x 2 34. d dx scsch21 xd − 2 1 | x |sx 2 1 1 35. d dx ssech21 xd − 2 1 xs1 2 x 2 36. d dx scoth21 xd − 1 1 2 x 2 Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it

REFERENCE page 6 TABLE OF INTEGRALS Basic Forms 1.udo =uodu 11.csc u cotu du =-cscu+C 2∫rh= ++Cn-1 12.tan u du In lsec ul+c 3∫鲁-alul+c 13.cot u du In |sin u+C 4∫e'd=e+c 14.sec u du In sec u+tanu+C 15.csc u du -In cscu cotu+C 6.∫in udu=-cosu+C 7.∫cosudu=sinw+C 8.sec'u du -tan u+C aj。aw片+c 9.∫eseu du--eotu+c 10.sec u tan u du-secu+C Forms Involving+a>0 2.+rd=后++gnu+v+)+c 2a∫r+T血-告+2的+r-g++)+C -du-VaiFui-aln a+@+匹|+C 26∫-片a+n-号++网+c j=++c a u du -+C a'u
REFERENCE page 6 Basic Forms 1. y u dv − uv 2 y v du 11. y csc u cot u du − 2csc u 1 C 2. y un du − un11 n 1 1 1 C, n ± 21 12. y tan u du − ln | sec u | 1 C 3. y du u − ln | u | 1 C 13. y cot u du − ln | sin u | 1 C 4. y e u du − e u 1 C 14. y sec u du − ln | sec u 1 tan u | 1 C 5. y bu du − bu ln b 1 C 15. y csc u du − ln | csc u 2 cot u | 1 C 6. y sin u du − 2cos u 1 C 16. y du sa2 2 u2 − sin21 u a 1 C, a . 0 7. y cos u du − sin u 1 C 17. y du a2 1 u2 − 1 a tan21 u a 1 C 8. y sec2 u du − tan u 1 C 18. y du usu2 2 a2 − 1 a sec21 u a 1 C 9. y csc2 u du − 2cot u 1 C 19. y du a2 2 u2 − 1 2a ln Z u 1 a u 2 a Z 1 C 10. y sec u tan u du − sec u 1 C 20. y du u2 2 a2 − 1 2a ln Z u 2 a u 1 a Z 1 C Forms Involving sa2 1 u2 , a . 0 21. y sa2 1 u2 du − u 2 sa2 1 u2 1 a2 2 ln(u 1 sa2 1 u2 ) 1 C 22. y u2 sa2 1 u2 du − u 8 sa2 1 2u2 d sa2 1 u2 2 a4 8 ln(u 1 sa2 1 u2 ) 1 C 23. y sa2 1 u2 u du − sa2 1 u2 2 a ln Z a 1 sa2 1 u2 u Z 1 C 24. y sa2 1 u2 u2 du − 2 sa2 1 u2 u 1 ln(u 1 sa2 1 u2 ) 1 C 25. y du sa2 1 u2 − ln(u 1 sa2 1 u2 ) 1 C 26. y u2 du sa2 1 u2 − u 2 sa2 1 u2 2 a2 2 ln(u 1 sa2 1 u2 ) 1 C 27. y du usa2 1 u2 − 2 1 a ln Z sa2 1 u2 1 a u Z 1 C 28. y du u2 sa2 1 u2 − 2 sa2 1 u2 a2 u 1 C 29. y du sa2 1 u2 d 3y2 − u a2 sa2 1 u2 1 C TABLE OF INTEGRALS Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it

REFERENCE page 7 TABLE OF INTEGRALS Forms Involving va-u.a>0 30.∫-=号后-+gsim+C 3∫A@-rh-营r-后-r+g如片+c 32T山-0-7-an+a-严|+c n.j-rh=长or-oi0-+答如+c t uryc Forms Involvingvu-a,a>0 8∫原-Ga-片原--受u+原-@列+C 4o∫2-aa-gar2-a的-a-galu+m-al+c 41.「-a血=-a-aow品+C a 4ajo德a=l+aa1+c (continued)
(continued) Cut here and keep for reference Forms Involving sa2 2 u2 , a . 0 30. y sa2 2 u2 du − u 2 sa2 2 u2 1 a2 2 sin21 u a 1 C 31. y u2 sa2 2 u2 du − u 8 s2u2 2 a2 d sa2 2 u2 1 a4 8 sin21 u a 1 C 32. y sa2 2 u2 u du − sa2 2 u2 2 a ln Z a 1 sa2 2 u2 u Z 1 C 33. y sa2 2 u2 u2 du − 2 1 u sa2 2 u2 2 sin21 u a 1 C 34. y u2 du sa2 2 u2 − 2 u 2 sa2 2 u2 1 a2 2 sin21 u a 1 C 35. y du usa2 2 u2 − 2 1 a ln Z a 1 sa2 2 u2 u Z 1 C 36. y du u2 sa2 2 u2 − 2 1 a2 u sa2 2 u2 1 C 37. y sa2 2 u2 d 3y2 du − 2 u 8 s2u2 2 5a2 dsa2 2 u2 1 3a4 8 sin21 u a 1 C 38. y du sa2 2 u2 d 3y2 − u a2 sa2 2 u2 1 C Forms Involving su2 2 a2 , a . 0 39. y su2 2 a2 du − u 2 su2 2 a2 2 a2 2 ln | u 1 su2 2 a2 | 1 C 40. y u2 su2 2 a2 du − u 8 s2u2 2 a2 d su2 2 a2 2 a4 8 ln | u 1 su2 2 a2 | 1 C 41. y su2 2 a2 u du − su2 2 a2 2 a cos21 a | u | 1 C 42. y su2 2 a2 u2 du − 2 su2 2 a2 u 1 ln | u 1 su2 2 a2 | 1 C 43. y du su2 2 a2 − ln | u 1 su2 2 a2 | 1 C 44. y u2 du su2 2 a2 − u 2 su2 2 a2 1 a2 2 ln | u 1 su2 2 a2 | 1 C 45. y du u2 su2 2 a2 − su2 2 a2 a2 u 1 C 46. y du su2 2 a2 d 3y2 − 2 u a2 su2 2 a2 1 C TABLE OF INTEGRALS REFERENCE page 7 Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it

REFERENCE page 8 TABLE OF INTEGRALS Forms Involving a+bu ∫e+-ala++C ∫+-+++a+c 51.o latal+c 2 54.∫va+md血=16u-2aa+bun+C 5级∫后忌w-2++c 6∫高+-6+而+C Ja+bu-va j店治+ +C.ifa>0 名mg+cw0 2 0∫g-26+而+岛 a∫-+品而 2「 ∫na+m血=2+a+a侧n-m∫-a+m 益晋德 2na u du a+bm_b2n-3fd ∫品而∫而
Forms Involving a 1 bu 47. y u du a 1 bu − 1 b2 (a 1 bu 2 a ln | a 1 bu |) 1 C 48. y u2 du a 1 bu − 1 2b3 fsa 1 bud 2 2 4asa 1 bud 1 2a2 ln| a 1 bu |g 1 C 49. y du usa 1 bud − 1 a ln Z u a 1 bu Z 1 C 50. y du u2 sa 1 bud − 2 1 au 1 b a2 ln Z a 1 bu u Z 1 C 51. y u du sa 1 bud 2 − a b2 sa 1 bud 1 1 b2 ln | a 1 bu | 1 C 52. y du usa 1 bud 2 − 1 asa 1 bud 2 1 a2 ln Z a 1 bu u Z 1 C 53. y u2 du sa 1 bud 2 − 1 b3 Sa 1 bu 2 a2 a 1 bu 2 2a ln | a 1 bu |D 1 C 54. y usa 1 bu du − 2 15b2 s3bu 2 2adsa 1 bud 3y2 1 C 55. y u du sa 1 bu − 2 3b2 sbu 2 2adsa 1 bu 1 C 56. y u2 du sa 1 bu − 2 15b3 s8a2 1 3b2 u2 2 4abudsa 1 bu 1 C 57. y du usa 1 bu − 1 sa ln Z sa 1 bu 2 sa sa 1 bu 1 sa Z 1 C, if a . 0 − 2 s2a tan21 Î a 1 bu 2a 1 C, if a , 0 58. y sa 1 bu u du − 2sa 1 bu 1 a y du usa 1 bu 59. y sa 1 bu u2 du − 2 sa 1 bu u 1 b 2 y du usa 1 bu 60. y un sa 1 bu du − 2 bs2n 1 3d Fun sa 1 bud 3y2 2 na y un21 sa 1 bu duG 61. y un du sa 1 bu − 2un sa 1 bu bs2n 1 1d 2 2na bs2n 1 1d y un21 du sa 1 bu 62. y du un sa 1 bu − 2 sa 1 bu asn 2 1dun21 2 bs2n 2 3d 2asn 2 1d y du un21 sa 1 bu TABLE OF INTEGRALS REFERENCE page 8 Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it

REFERENCE page 9 TABLE OF INTEGRALS Trigonometric Forms 63.sin'u du=uisin 2u+C 6jmuh-omri-小mrh 64.cos'u duu+sin 2u+c 65.tan'u du tan u-u+C B8.fceocc 66.cotu du --cotu -u+C 2(a-b) 67.sin'u du(2+sin2u)cos u+C 2(a+b) 68.cos'u du2+cosu)sin u+C 81.sin au cos bud山-cosa-be-csa+b加+c 2a-b) 2(a+b 69.tan'u du=tan'u In cosul+C 82.u sin u du sin u -u cosu+C 70.coP'u du-co'u-In sinul+c 83.u cos udu=cosu+usin u+C 71.sec'u du=sec u tanu+sec u ++C 84.u"sin u du =-u"cosu+n u cos u du 72.csc'u du=csc u cotu+csc u-cotu+C 85.u"cos udu u"sin u-n u sin u du nnh=in+”∫sra加 6nosh-出e兰+∫rwuh n+加 sin cos sin'u 雅十用 n十m 75jmwd=-小m nverse Trigonometric Forms 87.sin-'udu usin++C 88.cos-'u du u cos-u-1-u+C 89.tan-'u du utan-u-In(1+u2)+C 4 cos-luuI
(continued) Cut here and keep for reference TABLE OF INTEGRALS REFERENCE page 9 Trigonometric Forms 63. y sin2 u du − 1 2 u 2 1 4 sin 2u 1 C 76. y cot n u du − 21 n 2 1 cot n21 u 2 y cot n22 u du 64. y cos2 u du − 1 2 u 1 1 4 sin 2u 1 C 77. y secn u du − 1 n 2 1 tan u secn22 u 1 n 2 2 n 2 1 y secn22 u du 65. y tan2 u du − tan u 2 u 1 C 78. y cscn u du − 21 n 2 1 cot u cscn22 u 1 n 2 2 n 2 1 y cscn22 u du 66. y cot2 u du − 2cot u 2 u 1 C 79. y sin au sin bu du − sin sa 2 bdu 2sa 2 bd 2 sin sa 1 bdu 2sa 1 bd 1 C 67. y sin3 u du − 21 3 s2 1 sin2 ud cos u 1 C 80. y cos au cos bu du − sin sa 2 bdu 2sa 2 bd 1 sin sa 1 bdu 2sa 1 bd 1 C 68. y cos3 u du − 1 3 s2 1 cos2 ud sin u 1 C 81. y sin au cos bu du − 2 cos sa 2 bdu 2sa 2 bd 2 cos sa 1 bdu 2sa 1 bd 1 C 69. y tan3 u du − 1 2 tan2 u 1 ln | cos u | 1 C 82. y u sin u du − sin u 2 u cos u 1 C 70. y cot3 u du − 21 2 cot2 u 2 ln | sin u | 1 C 83. y u cos u du − cos u 1 u sin u 1 C 71. y sec3 u du − 1 2 sec u tan u 1 1 2 ln | sec u 1 tan u | 1 C 84. y un sin u du − 2un cos u 1 n y un21 cos u du 72. y csc3 u du − 21 2 csc u cot u 1 1 2 ln | csc u 2 cot u | 1 C 85. y un cos u du − un sin u 2 n y un21 sin u du 73. y sinn u du − 2 1 n sinn21 u cos u 1 n 2 1 n y sinn22 u du 86. y sinn u cosmu du − 2 sinn21 u cosm11 u n 1 m 1 n 2 1 n 1 m y sinn22 u cosmu du 74. y cosn u du − 1 n cosn21 u sin u 1 n 2 1 n y cosn22 u du − sinn11 u cosm21 u n 1 m 1 m 2 1 n 1 m y sinn u cosm22 u du 75. y tann u du − 1 n 2 1 tann21 u 2 y tann22 u du Inverse Trigonometric Forms 87. y sin21 u du − u sin21 u 1 s1 2 u2 1 C 92. y u tan21 u du − u2 1 1 2 tan21 u 2 u 2 1 C 88. y cos21 u du − u cos21 u 2 s1 2 u2 1 C 93. y un sin21 u du − 1 n 1 1 Fun11 sin21 u 2 y un11 du s1 2 u2 G, n ± 21 89. y tan21 u du − u tan21 u 2 1 2 lns1 1 u2 d 1 C 94. y un cos21 u du − 1 n 1 1 Fun11 cos21 u 1 y un11 du s1 2 u2 G, n ± 21 90. y u sin21 u du − 2u2 2 1 4 sin21 u 1 us1 2 u2 4 1 C 95. y un tan21 u du − 1 n 1 1 Fun11 tan21 u 2 y un11 du 1 1 u 91. 2 G, n ± 21 y u cos21 u du − 2u2 2 1 4 cos21 u 2 us1 2 u2 4 1 C Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it

REFERENCE page 10 TABLE OF INTEGRALS Exponential and Logarithmic Forms 1o0.nud加=ulnu-u+C n∫rr咖--∫r咖 +1 1o1.∫rhn血-a+pa+)a"-)+C a.∫esn=云+a-bos侧+C 1o2.c e 9.ecos hu d血=a+cos b+bsin侧)+C Hyperbolic Forms 103.sinh u du -coshc 108.csch u du In 104.cosh u du sinh u+C 109.sech'u du=tanh u+C 105.tanh udu=In coshu+C 110.csch'u du =-coth u+C 106.coth udu=In sinh uc 111.sech u tanh u du =-sechu+C 107.sech u du tan-sinhu+c 112.csch u coth u du =-csch u+C Forms Involving 2au -u,a>0 n∫m--"2m-+号ms(e。)+c --2-g2am+号w(e)+g 5.j2,正-v2m-+am-(e。)+c 6j@-2@-w(e)+d 2 du 2m-+c
REFERENCE page 10 Exponential and Logarithmic Forms 96. y ueau du − 1 a2 sau 2 1deau 1 C 100. y ln u du − u ln u 2 u 1 C 97. y un eau du − 1 a un eau 2 n a y un21 eau du 101. y un ln u du − un11 sn 1 1d 2 fsn 1 1d ln u 2 1g 1 C 98. y eau sin bu du − eau a2 1 b2 sa sin bu 2 b cos bud 1 C 102. y 1 u ln u du − ln | ln u | 1 C 99. y eau cos bu du − eau a2 1 b2 sa cos bu 1 b sin bud 1 C Hyperbolic Forms 103. y sinh u du − cosh u 1 C 108. y csch u du − ln | tanh 1 2 u | 1 C 104. y cosh u du − sinh u 1 C 109. y sech2 u du − tanh u 1 C 105. y tanh u du − ln cosh u 1 C 110. y csch2 u du − 2coth u 1 C 106. y coth u du − ln | sinh u | 1 C 111. y sech u tanh u du − 2sech u 1 C 107. y sech u du − tan21 | sinh u | 1 C 112. y csch u coth u du − 2csch u 1 C Forms Involving s2au 2 u2 , a . 0 113. y s2au 2 u2 du − u 2 a 2 s2au 2 u2 1 a2 2 cos21 S a 2 u a D 1 C 114. y us2au 2 u2 du − 2u2 2 au 2 3a2 6 s2au 2 u2 1 a3 2 cos21 S a 2 u a D 1 C 115. y s2au 2 u2 u du − s2au 2 u2 1 a cos21 S a 2 u a D 1 C 116. y s2au 2 u2 u2 du − 2 2s2au 2 u2 u 2 cos21 S a 2 u a D 1 C 117. y du s2au 2 u2 − cos21 S a 2 u a D 1 C 118. y u du s2au 2 u2 − 2s2au 2 u2 1 a cos21 S a 2 u a D 1 C 119. y u2 du s2au 2 u2 − 2 su 1 3ad 2 s2au 2 u2 1 3a2 2 cos21 S a 2 u a D 1 C 120. y du us2au 2 u2 − 2 s2au 2 u2 au 1 C PP TABLE OF INTEGRALS Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it