
数值分析 第三讲线性最小二乘问题 线性最小二乘问题的求解方法 目录 3.1问题介绍 3.2 Householder变换和Givens变换 3.3QR分解 3.4奇异值分解 3.5线性最小二乘问题的求解方法 https://math.ecnu.edu.cn/-jypan/Teaching/NA
数值分析 第三讲 线性最小二乘问题 线性最小二乘问题的求解方法 3.1 问题介绍 3.2 Householder 变换和 Givens 变换 3.3 QR 分解 3.4 奇异值分解 3.5 线性最小二乘问题的求解方法 目录 https://math.ecnu.edu.cn/~jypan/Teaching/NA

3-5 线性最小二乘问题的求解方法 3.5线性最小二乘问题的求解方法 3.5.1正规方程 3.5.2 Cholesky分解法 3.5.3QR分解法 3.5.4SVD分解法 潘建瑜@MATH.ECNU https://math.ecnu.edu.cn/-jypan/Teaching/NA
3-5 线性最小二乘问题的求解方法 3.5 线性最小二乘问题的求解方法 3.5.1 正规方程 3.5.2 Cholesky 分解法 3.5.3 QR 分解法 3.5.4 SVD 分解法 潘建瑜 @MATH.ECNU https://math.ecnu.edu.cn/~jypan/Teaching/NA

3-5-1正规方程 min llAx -bll? x∈Rn 定理设A∈Rmxn(m≥n),则x*∈R”是线性最小二乘问题的解当且仅当残量r= b-Ax与Ran(A)(值域)正交,即x*是下面的正规方程(或法方程)的解 AT(b-A)=0AT Ax=ATb. (3.1) (板书)】 http://nath.ecnu.edu.cn/-jypan 3/20
3-5-1 正规方程 min x∈Rn ∥Ax − b∥ 2 2 定理 设 A ∈ R m×n (m ≥ n), 则 x∗ ∈ R n 是线性最小二乘问题的解当且仅当残量 r = b − Ax∗ 与 Ran(A) (值域) 正交, 即 x∗ 是下面的正规方程 (或法方程) 的解 A ⊺ (b − Ax) = 0 或 A ⊺ Ax = A ⊺ b. (3.1) (板书) http://math.ecnu.edu.cn/~jypan 3/20

解的存在性与唯一性 由于 AbE Ran(AT)=Ran(AT A), 因此正规方程ATAx=ATb是相容(consistent)的,即最小二乘解总是存在的, http://nath.ecnu.edu.cn/-jypan 4/20
解的存在性与唯一性 由于 A ⊺ b ∈ Ran(A ⊺ ) = Ran(A ⊺ A), 因此正规方程 A ⊺Ax = A ⊺ b 是相容 (consistent) 的, 即 最小二乘解总是存在的. 定理 设 A ∈ R m×n (m ≥ n), 则 A ⊺A 对称正定当且仅当 A 是列满秩的, 即 rank(A) = n. 此时, 线性最小二乘问题的解是唯一的, 其表达式为 x∗ = (A ⊺ A) −1A ⊺ b. http://math.ecnu.edu.cn/~jypan 4/20

解的存在性与唯一性 由于 ATbERan(AT)=Ran(ATA), 因此正规方程ATAx=ATb是相容(consistent)的,即最小二乘解总是存在的, 定理设A∈Rmxn(m≥n),则ATA对称正定当且仅当A是列满秩的,即rank(A)=n. 此时,线性最小二乘问题的解是唯一的,其表达式为 .=(ATA)-1ATb. http://nath.ecnu.edu.cn/-jypan 4/20
解的存在性与唯一性 由于 A ⊺ b ∈ Ran(A ⊺ ) = Ran(A ⊺ A), 因此正规方程 A ⊺Ax = A ⊺ b 是相容 (consistent) 的, 即 最小二乘解总是存在的. 定理 设 A ∈ R m×n (m ≥ n), 则 A ⊺A 对称正定当且仅当 A 是列满秩的, 即 rank(A) = n. 此时, 线性最小二乘问题的解是唯一的, 其表达式为 x∗ = (A ⊺ A) −1A ⊺ b. http://math.ecnu.edu.cn/~jypan 4/20
最小二乘解的几何含义 根据最小二乘问题与正规方程的关系,我们可以把b 6 写成 b-Ax Ran(A) b=Ax+r,其中r⊥Ran(A): Ax. 所以Ax*就是b在Ran(A)上的正交投影,见右图 多需要指出的是,最小二乘解可能并不唯一,但上述分解是唯一的, http://math.ecnu.edu.cn/-jypan 5/20
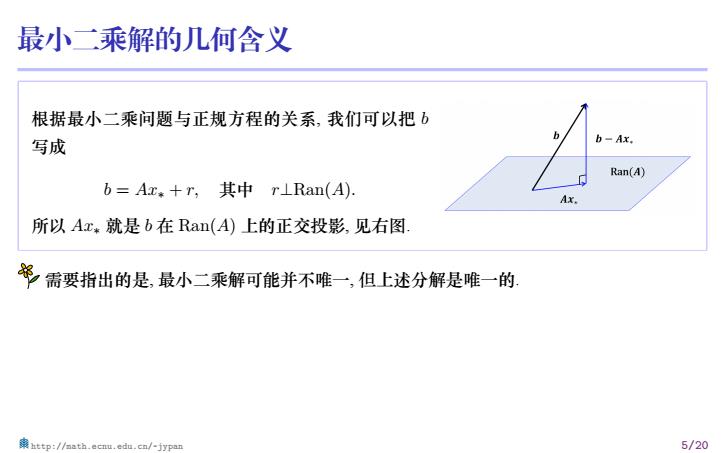
最小二乘解的几何含义 根据最小二乘问题与正规方程的关系, 我们可以把 b 写成 b = Ax∗ + r, 其中 r⊥Ran(A). 所以 Ax∗ 就是 b 在 Ran(A) 上的正交投影, 见右图. 需要指出的是, 最小二乘解可能并不唯一, 但上述分解是唯一的. http://math.ecnu.edu.cn/~jypan 5/20

3-5-2 Cholesky分解法 多当A列满秩时,我们就可以使用Cholesky分解来求解正规方程 http://nath.ecnu.edu.cn/-jypan 6/20
3-5-2 Cholesky 分解法 当 A 列满秩时, 我们就可以使用 Cholesky 分解来求解正规方程. 计算复杂度 计算 A ⊺A: → mn 2 % 只需计算下三角或上三角部分 计算 Cholesky 分解: → 1 3 n 3 回代求解: → O(n 2 ) 总的运算量大约为 mn 2 + 1 3 n 3 + O(n 2 ) http://math.ecnu.edu.cn/~jypan 6/20

3-5-2 Cholesky分解法 多当A列满秩时,我们就可以使用Cholesky分解来求解正规方程. 计算复杂度 O计算ATA: mn2%只需计算下三角或上三角部分 )计算Cholesky分解: → ⑦回代求解:→ 0(m2) 总的运算大的为m2+行+0问 http://math.ecnu.edu.cn/-jypan 6/20
3-5-2 Cholesky 分解法 当 A 列满秩时, 我们就可以使用 Cholesky 分解来求解正规方程. 计算复杂度 计算 A ⊺A: → mn2 % 只需计算下三角或上三角部分 计算 Cholesky 分解: → 1 3 n 3 回代求解: → O(n 2 ) 总的运算量大约为 mn2 + 1 3 n 3 + O(n 2 ) http://math.ecnu.edu.cn/~jypan 6/20

Cholesky分解求解正规方程的优缺点 优点:运算量最小,简单直观 缺点:A「A的条件数是A的平方,对于病态问题,不建议使用 http://math.ecnu.edu.cn/-jypan 7/20
Cholesky 分解求解正规方程的优缺点 优点: 运算量最小, 简单直观. 缺点: A ⊺A 的条件数是 A 的平方, 对于病态问题, 不建议使用. 例 设 A = 1 1 1 ε ε ε , 则 A ⊺A = 1 + ε 2 1 1 1 1 + ε 2 1 1 1 1 + ε 2 . 记 εu 为机器精度, 则当 εu < ε < √ εu 时有 ε 2 < εu, 由于舍入误差的原因, 通过浮点 运算计算得到的 A ⊺A 是奇异的. 但我们注意到 A 是满秩的. http://math.ecnu.edu.cn/~jypan 7/20

Cholesky分解求解正规方程的优缺点 ⊙优点:运算量最小,简单直观 缺点:A「A的条件数是A的平方,对于病态问题,不建议使用 111 1+e2 1 例 设A= 1+e2 都记em为机器精度,则当eu<e<VE时有e2<eu,由于舍入误差的原因,通过浮点 运算计算得到的A「A是奇异的.但我们注意到A是满秩的 http://math.ecnu.edu.cn/-jypan 7/20
Cholesky 分解求解正规方程的优缺点 优点: 运算量最小, 简单直观. 缺点: A ⊺A 的条件数是 A 的平方, 对于病态问题, 不建议使用. 例 设 A = 1 1 1 ε ε ε , 则 A ⊺A = 1 + ε 2 1 1 1 1 + ε 2 1 1 1 1 + ε 2 . 记 εu 为机器精度, 则当 εu < ε < √ εu 时有 ε 2 < εu, 由于舍入误差的原因, 通过浮点 运算计算得到的 A ⊺A 是奇异的. 但我们注意到 A 是满秩的. http://math.ecnu.edu.cn/~jypan 7/20