
数值分析 第二讲线性方程组的直接解法 扰动分析·解的改进 目录 2.1 Gauss消去法 2.2矩阵分解法 2.3扰动分析 AAYIAA 2.4解的改进* https://math.ecnu.edu.cn/-jypan/Teaching/NA 潘建瑜@MATH.ECNU
数值分析 第二讲 线性方程组的直接解法 扰动分析 • 解的改进 2.1 Gauss 消去法 2.2 矩阵分解法 2.3 扰动分析 2.4 解的改进 * 目录 https://math.ecnu.edu.cn/~jypan/Teaching/NA 潘建瑜 @MATH.ECNU

2-3|扰动分析 2.3扰动分析 2.3.1矩阵条件数 2.3.2条件数与扰动分析 https://math.ecnu.edu.cn/-jypan/Teaching/NA
2-3 扰动分析 2.3 扰动分析 2.3.1 矩阵条件数 2.3.2 条件数与扰动分析 https://math.ecnu.edu.cn/~jypan/Teaching/NA

2-3-1 矩阵条件数 为什么要考虑扰动分析 除了数据误差和截断误差外,在用计算机进行数值计算时,每次运算(加减乘除等)还会 产生舍入误差.对于大规模问题,实际运算次数往往非常巨大,因此直接分析舍入误差比 较复杂,而且得到的结果往往不一定能反映实际计算情况.当前一种比较实用的误差分 析方法是将舍入误差看作是对原始数据的扰动,即将其归结到数据误差中,这样就可以在 很大程度上简化误差分析过程.这种误差分析方法称为向后误差分析, 病态线性方程组/病态矩阵 考虑线性方程组Ax=b,如果A或b的微小变化(也称为扰动)会导致解的巨大变化,则 称此线性方程组是病态的,反之则是良态的 http://math.ecnu.edu.cn/-jypan 3/22
2-3-1 矩阵条件数 为什么要考虑扰动分析 除了数据误差和截断误差外, 在用计算机进行数值计算时, 每次运算 (加减乘除等) 还会 产生舍入误差. 对于大规模问题, 实际运算次数往往非常巨大, 因此直接分析舍入误差比 较复杂, 而且得到的结果往往不一定能反映实际计算情况. 当前一种比较实用的误差分 析方法是将舍入误差看作是对原始数据的扰动, 即将其归结到数据误差中, 这样就可以在 很大程度上简化误差分析过程. 这种误差分析方法称为向后误差分析. 病态线性方程组/病态矩阵 考虑线性方程组 Ax = b, 如果 A 或 b 的微小变化 (也称为 扰动) 会导致解的巨大变化, 则 称此线性方程组是 病态 的, 反之则是 良态 的. http://math.ecnu.edu.cn/~jypan 3/22

病态线性方程组举例 例考虑线性方程组Ax=b,其中A= →解为x= 20 http://math.ecnu.edu.cn/-jypan 4/22
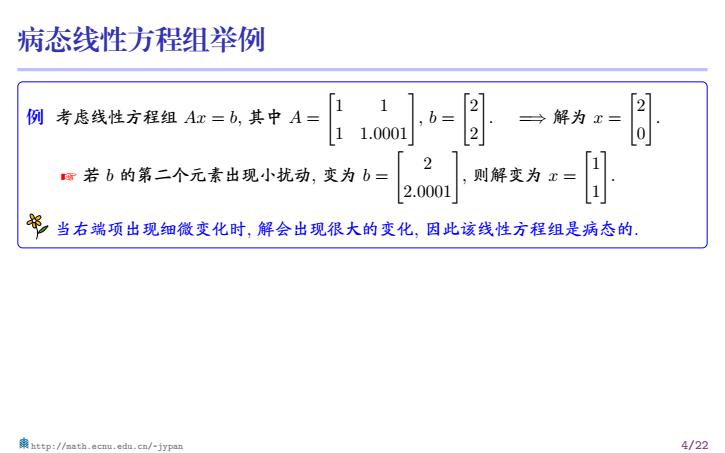
病态线性方程组举例 例 考虑线性方程组 Ax = b, 其中 A = [ 1 1 1 1.0001] , b = [ 2 2 ] . =⇒ 解为 x = [ 2 0 ] . Z 若 b 的第二个元素出现小扰动, 变为 b = [ 2 2.0001 ] , 则解变为 x = [ 1 1 ] . 当右端项出现细微变化时, 解会出现很大的变化, 因此该线性方程组是病态的. 怎样判断一个线性方程组是否病态? 对于线性方程组而言, 问题是否变态主要取决于 系数矩阵是否病态 . 判断一个矩阵是否病态的一个重要指标是 矩阵条件数 . http://math.ecnu.edu.cn/~jypan 4/22
病态线性方程组举例 1 例考虑线性方程组Ax=b,其中A= 1 ,b= 1 →解为x= 1.0001 22 20 都当右端项出现细微变化时,解会出现很大的变化,因此该线性方程组是病态的, http://nath.ecnu.edu.cn/-jypan 4/22
病态线性方程组举例 例 考虑线性方程组 Ax = b, 其中 A = [ 1 1 1 1.0001] , b = [ 2 2 ] . =⇒ 解为 x = [ 2 0 ] . Z 若 b 的第二个元素出现小扰动, 变为 b = [ 2 2.0001] , 则解变为 x = [ 1 1 ] . 当右端项出现细微变化时, 解会出现很大的变化, 因此该线性方程组是病态的. 怎样判断一个线性方程组是否病态? 对于线性方程组而言, 问题是否变态主要取决于 系数矩阵是否病态 . 判断一个矩阵是否病态的一个重要指标是 矩阵条件数 . http://math.ecnu.edu.cn/~jypan 4/22

病态线性方程组举例 11 1 例考虑线性方程组Ax=b,其中A= b- 22 →解为x= 20 者的第二个元本夏本发美为市一b小 当右端项出现细微变化时,解会出现很大的变化,因此该线性方程组是病态的. 怎样判断一个线性方程组是否病态? 对于线性方程组而言,问题是否变态主要取决于系数矩阵是否病态 判断一个矩阵是否病态的一个重要指标是矩阵条件数 http://nath.ecnu.edu.cn/-jypan 4/22
病态线性方程组举例 例 考虑线性方程组 Ax = b, 其中 A = [ 1 1 1 1.0001] , b = [ 2 2 ] . =⇒ 解为 x = [ 2 0 ] . Z 若 b 的第二个元素出现小扰动, 变为 b = [ 2 2.0001] , 则解变为 x = [ 1 1 ] . 当右端项出现细微变化时, 解会出现很大的变化, 因此该线性方程组是病态的. 怎样判断一个线性方程组是否病态? 对于线性方程组而言, 问题是否变态主要取决于 系数矩阵是否病态 . 判断一个矩阵是否病态的一个重要指标是 矩阵条件数 . http://math.ecnu.edu.cn/~jypan 4/22

矩阵条件数 定义设A非奇异,‖·‖是任一算子范数,则称 k(A)≌A-1‖·‖A 为A的条件数. http://nath.ecnu.edu.cn/-jypan 5/22
矩阵条件数 定义 设 A 非奇异, ∥ · ∥ 是任一算子范数, 则称 κ(A) ≜ ∥A −1 ∥ · ∥A∥ 为 A 的 条件数. ✍ 常用的矩阵条件数有 κ2(A) ≜ ∥A −1 ∥2 · ∥A∥2, κ1(A) ≜ ∥A −1 ∥1 · ∥A∥1, κ∞(A) ≜ ∥A −1 ∥∞ · ∥A∥∞. ✍ κ2(A) 也称为 谱条件数, 当 A 对称时, 有 κ2(A) = max 1≤i≤n |λi | min 1≤i≤n |λi | http://math.ecnu.edu.cn/~jypan 5/22

矩阵条件数 定义设A非奇异,川·‖是任一算子范数,则称 k(A)eIA-1I·IA 为A的条件数 常用的矩阵条件数有 2(A)≌Al2·IA2,1(A)≌A-1l1·Al1,o(A)≌IA-lo·A|o max 白2(A)也称为谱条件数,当A对称时,有 2(A)= 1≤isn min I≤2≤n http://nath.ecnu.edu.cn/-jypan 5/22
矩阵条件数 定义 设 A 非奇异, ∥ · ∥ 是任一算子范数, 则称 κ(A) ≜ ∥A −1 ∥ · ∥A∥ 为 A 的 条件数. ✍ 常用的矩阵条件数有 κ2(A) ≜ ∥A −1 ∥2 · ∥A∥2, κ1(A) ≜ ∥A −1 ∥1 · ∥A∥1, κ∞(A) ≜ ∥A −1 ∥∞ · ∥A∥∞. ✍ κ2(A) 也称为 谱条件数, 当 A 对称时, 有 κ2(A) = max 1≤i≤n |λi | min 1≤i≤n |λi | http://math.ecnu.edu.cn/~jypan 5/22

例计算前例中的系数矩阵A的条件数(A)和2(A), (-famn) 解通过直接计算可得 10001 -10000 所以 -10000 10000 k(A)=A‖o·A-1‖o≈4×104. 由于A是对称的,且A的特征值为 A1A=2.001±V2.002-0.004 >0, 2 所以 2(A)= 入ma≈4×104 入min http://math.ecnu.edu.cn/-jypan 6/22
例 计算前例中的系数矩阵 A 的条件数 κ∞(A) 和 κ2(A). ( A = [ 1 1 1 1.0001]) 解. 通过直接计算可得 A−1 = [ 10001 −10000 −10000 10000 ] . 所以 κ∞(A) = ∥A∥∞ · ∥A −1 ∥∞ ≈ 4 × 104 . 由于 A 是对称的, 且 A 的特征值为 λ(A) = 2.0001 ± √ 2.00012 − 0.0004 2 > 0, 所以 κ2(A) = λmax λmin ≈ 4 × 104 . □ http://math.ecnu.edu.cn/~jypan 6/22

[1 -0.5 -0.57 1 例(条件数与特征值) 已知矩阵A= ∈Rnxn -0.5 1 [1 1.52 1.5m-27 2 2 2 1 2 直接计算可知A~1= 1 1.52 12 1.5 1 1 直接观察可知,1(A)和k(A)会随着n的增大而快速增长. http://math.ecnu.edu.cn/-jypan 7/22
例 (条件数与特征值 ) 已知矩阵 A = 1 − 0 . 5 · · · − 0 . 5 1 . . . ... . . . − 0 . 5 1 ∈ R n × n . 直接计算可知 A − 1 = 1 12 1 . 52 1 . 5 2 2 · · · 1 . 5 n − 2 2 1 12 1 . 52 . . . ... 1 . . . . . . 1 . 5 2 2 . . . 12 1 . 52 1 121 . 直接观察可知 , κ 1 ( A ) 和 κ ∞ ( A ) 会随着 n 的增大而快速增长 . http://math.ecnu.edu.cn/~jypan 7/22