
数值分析 第三讲线性最小二乘问题 奇异值分解(SVD) 目录 3.1问题介绍 3.2 Householder变换和Givens变换 3.3QR分解 3.4奇异值分解 3.5线性最小二乘问题的求解方法 https://math.ecnu.edu.cn/-jypan/Teaching/NA
数值分析 第三讲 线性最小二乘问题 奇异值分解 (SVD) 3.1 问题介绍 3.2 Householder 变换和 Givens 变换 3.3 QR 分解 3.4 奇异值分解 3.5 线性最小二乘问题的求解方法 目录 https://math.ecnu.edu.cn/~jypan/Teaching/NA

CLEVE'S CORNER Professor SVD BY CLEVE MOLER Stanford computer science professor Gene Golub has done more than anyone to make the singular value decomposition one of the most powerful and widely used tools in modern matrix computation. Gene Golub oC APR C AL IF OR NIA 7200s anying worm compuring can be aoda的&matn probiom PROF SVD THE LINEAR ALCEURA ND GOGLE William Kahan Formaimd住E7i4 osting po情ormeto M0情Co5t相o campure wi probablno侧 Tw numbvs'ridid of dea:mn cowfs Gee Golbse pae phogaped by Poksor PM Kmxrerbeg leiden Lhiventy

3-41 奇异值分解 3.4奇异值分解 3.4.1奇异值与奇异值分解 3.4.2奇异值的性质 潘建瑜@MATH.ECNU https://math.ecnu.edu.cn/-jypan/Teaching/NA SVD不仅是矩阵计算中的重要工具之一,也是图像处理、压缩感知、机器学习、数据科 学等领域的重要技术
3-4 奇异值分解 3.4 奇异值分解 3.4.1 奇异值与奇异值分解 3.4.2 奇异值的性质 潘建瑜 @MATH.ECNU https://math.ecnu.edu.cn/~jypan/Teaching/NA SVD 不仅是矩阵计算中的重要工具之一, 也是图像处理、压缩感知、机器学习、数据科 学等领域的重要技术

3-4-1奇异值与奇异值分解 定理设A∈Cmxn(m≥n),则存在酉矩阵U∈Cmxm和V∈Cnxn使得 U'AV v", (3.1) 其中∑=diag(a1,o2,,on)∈Rnxm,且 01≥02≥..20n≥0. 分解(3.1I)称为A的奇异值分解(SVD),而01,o2,,0n则称为A的奇异值. (板书)】 http://math.ecnu.edu.cn/-jypan 4/13
3-4-1 奇异值与奇异值分解 定理 设 A ∈ C m×n (m ≥ n), 则存在酉矩阵 U ∈ C m×m 和 V ∈ C n×n 使得 U ∗AV = [ Σ 0 ] 或 A = U [ Σ 0 ] V ∗ , (3.1) 其中 Σ = diag(σ1, σ2, . . . , σn) ∈ R n×n , 且 σ1 ≥ σ2 ≥ . . . ≥ σn ≥ 0. 分解 (3.1) 称为 A 的奇异值分解 (SVD ), 而 σ1, σ2, . . . , σn 则称为 A 的奇异值. (板书) 如果 A ∈ R m×n 是实矩阵, 则 U, V 也都可以是实矩阵. http://math.ecnu.edu.cn/~jypan 4/13

3-4-1奇异值与奇异值分解 定理设A∈Cmxn(m≥n,则存在酉矩阵U∈Cmxm和V∈Cnxn使得 (3.1) 其中2=diag(o1,o2,,on)∈Rmxm,且 01≥02≥.20n≥0. 分解(3.1)称为A的奇异值分解(SVD),而o1,02,,0n则称为A的奇异值. (板书)】 如果A∈Rmxn是实矩阵,则U,V也都可以是实矩阵 http://math.ecnu.edu.cn/-jypan 4/13
3-4-1 奇异值与奇异值分解 定理 设 A ∈ C m×n (m ≥ n), 则存在酉矩阵 U ∈ C m×m 和 V ∈ C n×n 使得 U ∗AV = [ Σ 0 ] 或 A = U [ Σ 0 ] V ∗ , (3.1) 其中 Σ = diag(σ1, σ2, . . . , σn) ∈ R n×n , 且 σ1 ≥ σ2 ≥ . . . ≥ σn ≥ 0. 分解 (3.1) 称为 A 的奇异值分解 (SVD ), 而 σ1, σ2, . . . , σn 则称为 A 的奇异值. (板书) 如果 A ∈ R m×n 是实矩阵, 则 U, V 也都可以是实矩阵. http://math.ecnu.edu.cn/~jypan 4/13

奇异值与特征值 A=U → AA=VΣ*2V,AA=U http://nath.ecnu.edu.cn/-jypan 5/13
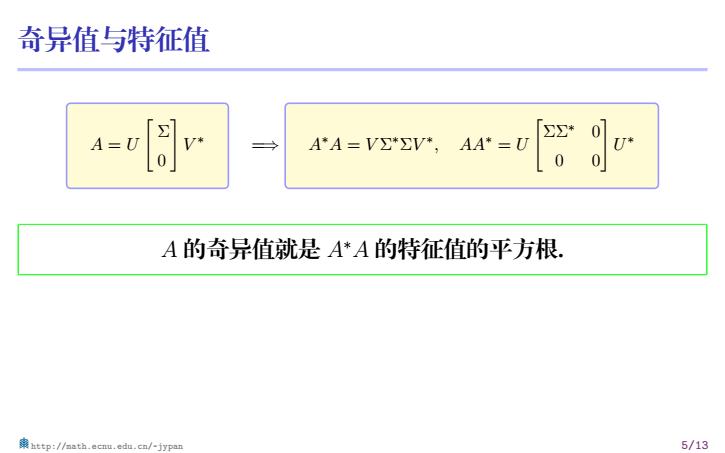
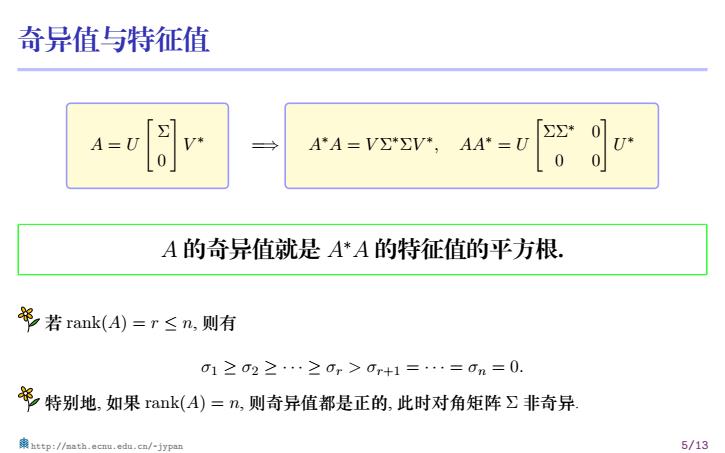
奇异值与特征值 A = U [ Σ 0 ] V ∗ =⇒ A ∗A = V Σ ∗ΣV ∗ , AA∗ = U [ ΣΣ∗ 0 0 0] U ∗ A 的奇异值就是 A∗A 的特征值的平方根. 若 rank(A) = r ≤ n, 则有 σ1 ≥ σ2 ≥ · · · ≥ σr > σr+1 = · · · = σn = 0. 特别地, 如果 rank(A) = n, 则奇异值都是正的, 此时对角矩阵 Σ 非奇异. http://math.ecnu.edu.cn/~jypan 5/13
奇异值与特征值 A=U V* ∑*( → A*A=V∑*∑V*,AA*=U 0 0 A的奇异值就是A*A的特征值的平方根, http://math.ecnu.edu.cn/-jypan 5/13
奇异值与特征值 A = U [ Σ 0 ] V ∗ =⇒ A ∗A = V Σ ∗ΣV ∗ , AA∗ = U [ ΣΣ∗ 0 0 0] U ∗ A 的奇异值就是 A∗A 的特征值的平方根. 若 rank(A) = r ≤ n, 则有 σ1 ≥ σ2 ≥ · · · ≥ σr > σr+1 = · · · = σn = 0. 特别地, 如果 rank(A) = n, 则奇异值都是正的, 此时对角矩阵 Σ 非奇异. http://math.ecnu.edu.cn/~jypan 5/13
奇异值与特征值 A=U → A'A=VE'EV,AA*=U A的奇异值就是A*A的特征值的平方根. 多若rank(A)=r≤n,则有 01≥022…≥0r>0+1=·=0n=0. 花特别地,如果rak(A)=n,则奇异值都是正的,此时对角矩阵Σ非奇异. http://nath.ecnu.edu.cn/-jypan 5/13
奇异值与特征值 A = U [ Σ 0 ] V ∗ =⇒ A ∗A = V Σ ∗ΣV ∗ , AA∗ = U [ ΣΣ∗ 0 0 0] U ∗ A 的奇异值就是 A∗A 的特征值的平方根. 若 rank(A) = r ≤ n, 则有 σ1 ≥ σ2 ≥ · · · ≥ σr > σr+1 = · · · = σn = 0. 特别地, 如果 rank(A) = n, 则奇异值都是正的, 此时对角矩阵 Σ 非奇异. http://math.ecnu.edu.cn/~jypan 5/13

奇异向量 A=U D* → AV=U A*U=[Σ,0]V 0 A=0u,i=1,2,..,n, A*=0v,i=1,2,,n, A*吃=0,i=n+1,n+2,.,m. 多矩阵U=仙1,2,,山n]的列向量称为A的左奇异向量 都矩阵V=心1,2,n的列向量称为A的右奇异向量 http://math.ecnu.edu.cn/-jypan 6/13
奇异向量 A = U [ Σ 0 ] V ∗ =⇒ AV = U [ Σ 0 ] , A∗U = [ Σ, 0 ] V Avi = σiui , i = 1, 2, . . . , n, A ∗ui = σivi , i = 1, 2, . . . , n, A ∗ui = 0, i = n + 1, n + 2, . . . , m. 矩阵 U = [u1, u2, . . . , um] 的列向量称为 A 的左奇异向量 矩阵 V = [v1, v2, . . . , vn] 的列向量称为 A 的右奇异向量 http://math.ecnu.edu.cn/~jypan 6/13

降阶SVD 台 Giuiv http://nath.ecnu.edu.cn/-jypan 7/13
降阶 SVD A = [ u1, . . . , um ] [ Σ 0 ] [ v1, . . . , vn ]∗ = σ1u1v ∗ 1 + σ2u2v ∗ 2 + · · · + σnunv ∗ n = ∑n i=1 σiuiv ∗ i 记 Un = [u1, u2, . . . , un] ∈ C m×n , 则 Un 是单位列正交矩阵 (即 U ∗ nUn = In×n), 且 A = UnΣV ∗ (3.2) 这就是 细 SVD (thin SVD ) 或 降阶 SVD (reduced SVD ). ✍ 有的文献将 (3.2) 称为奇异值分解. http://math.ecnu.edu.cn/~jypan 7/13