数值分析 第二讲线性方程组的直接解法 Gauss消去法·矩阵分解法 喜目录 2.1 Gauss消去法 2.2 矩阵分解法 2.3 扰动分析 2.4解的改进* 潘建瑜@MATH.ECNU https://math.ecnu.edu.cn/-jypan/Teaching/NA
数值分析 第二讲 线性方程组的直接解法 Gauss 消去法 • 矩阵分解法 2.1 Gauss 消去法 2.2 矩阵分解法 2.3 扰动分析 2.4 解的改进 * 目录 https://math.ecnu.edu.cn/~jypan/Teaching/NA 潘建瑜 @MATH.ECNU

2-1|Gaus消去法 2.1 Gauss消去法 2.1.1 Gauss消去过程(算法描述) 2.1.2运算量统计(计算复杂度) https://math.ecnu.edu.cn/-jypan/Teaching/NA
2-1 Gauss 消去法 2.1 Gauss 消去法 2.1.1 Gauss 消去过程 (算法描述) 2.1.2 运算量统计 (计算复杂度) https://math.ecnu.edu.cn/~jypan/Teaching/NA

Gauss消去法 图Gauss消去法的基本思想是消元 图早在2000年前,中国古代学者就提出了消元思想(记载在公元初《九章算术》方程 章中),Newton,Lagrange,Gauss,Jacobi等都对此做过研究, 图我们目前采用的算法描述方式是十九世纪三十年代后期才形成的 aussian elimination(GE)is the standard method Nicholas J.Higham Jfor solving a system of linear equations.As such, Royal Society it is one of the most ubiquitous numerical algorithms Royal Academy of Engineering and plays a fundamental role in scientific computation. Academia Europaea GE was known to the ancient Chinese!and is National Academy of Engineering familiar to many school children as the intuitively President of SIAM, natural method of eliminating variables from linear ACM Fellow,SIAM Fellow equations. Nicholas J.Higham.Gaussian elimination.WIREs Computational Statistics.3(2011).230-238. http://math.ecnu.edu.cn/-jypan 3/52
Gauss 消去法 Gauss 消去法的基本思想是消元. 早在 2000 年前, 中国古代学者就提出了消元思想(记载在公元初《九章算术》方程 章中), Newton, Lagrange, Gauss, Jacobi 等都对此做过研究. 我们目前采用的算法描述方式是十九世纪三十年代后期才形成的. http://math.ecnu.edu.cn/~jypan 3/52
个例子 例求解下面的线性方程组 x1-2x2+2x3=-2 2x1-3x2-3x3=4 4r1+x2+6x3=3. Gauss消去法:先写出增广矩阵,然后通过初等变换将其转换为阶梯形(上三角) 1 -2 2 2 ②-0×2 1-22-2 1 -2 2 -2 ③-×4 ⑥-②x9 2 -3 -3 4 0 1 -7 8 0 1 -7 8 6 3 09-2 11 0 061-61 通过回代求解可得 x3=-1,2=8+7x3=1,x1=-2+2x2-2xg=2. http://math.ecnu.edu.cn/-jypan 4/52
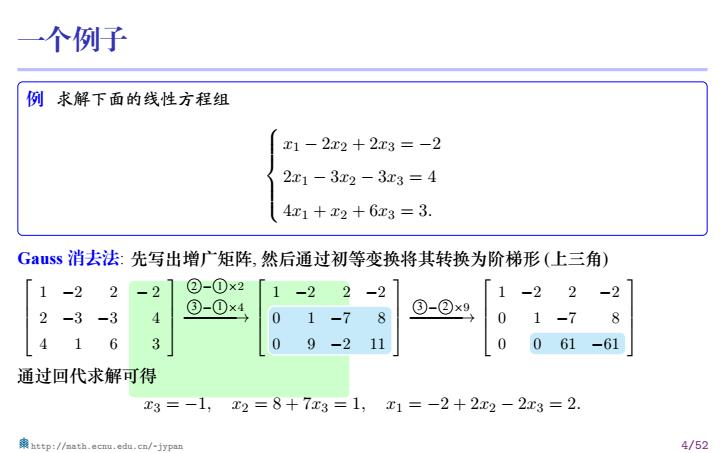
一个例子 例 求解下面的线性方程组 x1 − 2x2 + 2x3 = −2 2x1 − 3x2 − 3x3 = 4 4x1 + x2 + 6x3 = 3. Gauss 消去法: 先写出增广矩阵, 然后通过初等变换将其转换为阶梯形 (上三角) 1 −2 2 − 2 2 −3 −3 4 4 1 6 3 ⃝2 −⃝1 ×2 ⃝3 −⃝1 ×4 −−−−−−→ 1 −2 2 −2 0 1 −7 8 0 9 −2 11 ⃝3 −⃝2 ×9 −−−−−−→ 1 −2 2 −2 0 1 −7 8 0 0 61 −61 通过回代求解可得 x3 = −1, x2 = 8 + 7x3 = 1, x1 = −2 + 2x2 − 2x3 = 2. http://math.ecnu.edu.cn/~jypan 4/52

推广到一般线性方程 a11x1+a12x2+··+a1nxm=b1 a21x1十a22x2+·+a2mxn=b2 an11+an2T2+..+annEn on 高斯消去法的主要思路: 将系数矩阵A化为上三角矩阵,然后回代求解 A → http://nath.ecnu.edu.cn/-jypan 5/52
推广到一般线性方程 a11x1 + a12x2 + · · · + a1nxn = b1 a21x1 + a22x2 + · · · + a2nxn = b2 . . . . . . . . . . . . . . . . an1x1 + an2x2 + · · · + annxn = bn 高斯消去法的主要思路: 将系数矩阵 A 化为上三角矩阵, 然后回代求解 ✍ 高斯消去法是求解线性方程组的经典算法, 是线性代数的重要组成部分, 除了用于线 性方程组求解外, 还用于计算行列式、矩阵的秩、矩阵的逆等. http://math.ecnu.edu.cn/~jypan 5/52
推广到一般线性方程 a1121 a12x2++ainEn 61 a211+a22x2+...+a2n.tn b2 anlc1+an2x2+··+annEn=bn 高斯消去法的主要思路: 将系数矩阵A化为上三角矩阵,然后回代求解 A 凸高斯消去法是求解线性方程组的经典算法,是线性代数的重要组成部分,除了用于线 性方程组求解外,还用于计算行列式、矩阵的秩、矩阵的逆等 http://math.ecnu.edu.cn/-jypan 5/52
推广到一般线性方程 a11x1 + a12x2 + · · · + a1nxn = b1 a21x1 + a22x2 + · · · + a2nxn = b2 . . . . . . . . . . . . . . . . an1x1 + an2x2 + · · · + annxn = bn 高斯消去法的主要思路: 将系数矩阵 A 化为上三角矩阵, 然后回代求解 ✍ 高斯消去法是求解线性方程组的经典算法, 是线性代数的重要组成部分, 除了用于线 性方程组求解外, 还用于计算行列式、矩阵的秩、矩阵的逆等. http://math.ecnu.edu.cn/~jypan 5/52

2-1-1 Gauss消去过程 多写出相应算法,并编程实现 记增广矩阵 ) (1) 1) 011 012 0 (1) 022 (1) A)= 0 州 a ) ann 其中 =0j b=b, i,j=1,2,,n http://nath.ecnu.edu.cn/-jypan 6/52
2-1-1 Gauss 消去过程 写出相应算法, 并编程实现 记增广矩阵 A (1) = a (1) 11 a (1) 12 · · · a (1) 1n b (1) 1 a (1) 21 a (1) 22 · · · a (1) 2n b (1) 2 . . . . . . . . . . . . . . . a (1) n1 a (1) n2 · · · a (1) nn b (1) n , 其中 a (1) ij = aij , b(1) i = bi , i, j = 1, 2, . . . , n. http://math.ecnu.edu.cn/~jypan 6/52

第1步:消第1列 (1) 设唱≠0,计算1=霜i=2,3n对增广矩阵A0进行n-1次初等变换,即 011 依次将A1)的第i行(i>1)减去第1行的l1倍,将新得到的矩阵记为A②),即 (1) a12 (2) (2) A② 022 02m g 品 其中 =9-l1,b2=6-ab吧,ij=2,3n 00 http://math.ecnu.edu.cn/-jypan 7/52
第 1 步: 消第 1 列. 设 a (1) 11 ̸= 0 , 计算 li1 = a (1) i1 a (1) 11 , i = 2, 3, . . . , n. 对增广矩阵 A(1) 进行 n − 1 次初等变换, 即 依次将 A(1) 的第 i 行 (i > 1) 减去第 1 行的 li1 倍, 将新得到的矩阵记为 A(2) , 即 A (2) = a (1) 11 a (1) 12 · · · a (1) 1n b (1) 1 a (2) 22 · · · a (2) 2n b (2) 2 . . . . . . . . . . . . a (2) n2 · · · a (2) nn b (2) n , 其中 a (2) ij = a (1) ij − li1a (1) 1j , b(2) i = b (1) i − li1b (1) 1 , i, j = 2, 3, . . . , n. http://math.ecnu.edu.cn/~jypan 7/52

第2步:消第2列 (2) 设a2≠0,计算l2= ,i=34…n 依次将A②的第i行(i>2)减去第2行的 02 l2倍,将新得到的矩阵记为A③),即 a .(1) (1) 012 唱 01 四 (2) (2 (2) d22 023 02 A3)= ) 033 (2) a侧 a 周 其中 g=号-l号,6=9-lab2,ij=3,4,n http://math.ecnu.edu.cn/-jypan 8/52
第 2 步: 消第 2 列. 设 a (2) 22 ̸= 0 , 计算 li2 = a (2) i2 a (2) 22 , i = 3, 4, . . . , n. 依次将 A(2) 的第 i 行 (i > 2) 减去第 2 行的 li2 倍, 将新得到的矩阵记为 A(3) , 即 A (3) = a (1) 11 a (1) 12 a (1) 13 · · · a (1) 1n b (1) 1 a (2) 22 a (2) 23 · · · a (2) 2n b (2) 2 a (2) 33 · · · a (2) 3n b (3) 3 . . . . . . . . . . . . a (3) n3 · · · a (3) nn b (3) n , 其中 a (3) ij = a (2) ij − li2a (2) 2j , b(3) i = b (2) i − li2b (2) 2 , i, j = 3, 4, . . . , n. http://math.ecnu.edu.cn/~jypan 8/52

依此类推,经过k-1步后,可得新矩阵A(): .(1) (1) 01k A(k)= () () akk akn (2.1) a限 恩 第k步:消第k列, () 设Q手0,开算:资三大+L候次将4的的第i行>)减去第至 的1:倍,将新得到的矩阵记为Ak+1),矩阵元素的更新公式为 ag+=a9-au周,6+=b-lb,i,j=k+1,k+2,n. (2.2) http://math.ecnu.edu.cn/-jypan 9/52
依此类推, 经过 k − 1 步后, 可得新矩阵 A(k) : A (k) = a (1) 11 · · · a (1) 1k · · · a (1) 1n b (1) 1 . . . . . . . . . . . . a (k) kk · · · a (k) kn b (k) k . . . . . . . . . . . . a (k) nk · · · a (k) nn b (k) n , (2.1) 第 k 步: 消第 k 列. 设 a (k) kk ̸= 0 , 计算 lik = a (k) ik a (k) kk , i = k + 1, . . . , n. 依次将 A(k) 的第 i 行 (i > k) 减去第 k 行 的 lik 倍, 将新得到的矩阵记为 A(k+1) , 矩阵元素的更新公式为 a (k+1) ij = a (k) ij − lika (k) kj , b(k+1) i = b (k) i − likb (k) k , i, j = k + 1, k + 2, . . . , n. (2.2) http://math.ecnu.edu.cn/~jypan 9/52