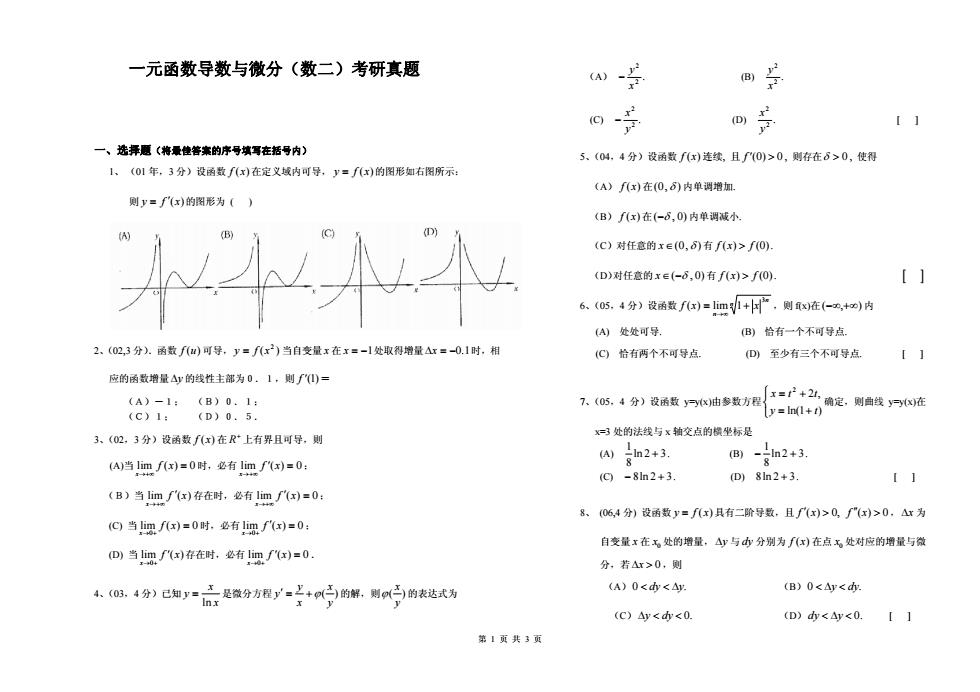
一元函数导数与微分(数二)考研真题 w 回三 一、选择题(将最佳答案的序号填写在括号内) 5、(04,4分)设函数fx)连续,且f(0)>0,则存在6>0,使得 1、(01年,3分)设函数f(x)在定义域内可导,y=fx)的图形如右图所示: (A)f八x)在(0,6)内单调增. 则y=f(x)的图形为() (B)f(x)在(-6,0)内单调减小 (C)对任意的x∈(0,6)有f(x)>f0) (D)对任意的x∈(-6,0)有f(x)>f0). [1 6、(05,4分)设函数f)=im小+,则四在(-,切)内 (A)处处可导. B)恰有一个不可导点 2.(02,3分).函数f(u)可导,y=fx2)当自变量x在x=- 1处取得增量△x=-0.1时,相 (C)恰有两个不可导点 D)至少有三个不可导点 II 应的函数增量△的线性主部为0.1,则∫(0)= (A)-1:(B)0.1: 不(0.4分设质数只油参数方程红心2确定,则线)只在 (C)1:(D)0.5. y=In(1+1)" 3、(02,3分)设函数f(x)在R*上有界且可导,则 Xx=处的法线与x轴交点的横坐标是 An2+3. ®-n2+3. (A)当1imf(x)=0时,必有1imf'(x)=0: (C-8lh2+3. D)81n2+3. II (B)当imf')存在时,必有limf八x)=0: 8、(06,4分)设函数y=f(x)具有二阶导数,且f(x)>0,f"(x)>0,△x为 (©当5mfx)=0时.必有1mfx)=0: 自变量x在无处的增量,△y与少分别为f(x)在点无处对应的增量与微 D当mf(x)存在时,必有1imfy=0. 分,若△r>0,则 小@3.4分》已知y产是微分方程)/e上+p宁的解、则白的表达式为 (A)0<d<△. (B)0<△y<. (C)△y<<0. (D)d<4y<0.I1 第1页共3页
一元函数导数与微分(数二)考研真题 第 页 共 页 f xfy )( 一、选择题(将最佳答案的序号填写在括号内) 1、 (01 年,3 分)设函数 在定义域内可导, x)( 的图形如右图所示: 则 的图形为 xfy )( ( ) 2、(02,3 分).函数 uf )( 可导, 当自变量 ) 2 y (xf x 在 处取得增量 时,相 应的函数增量 的线性主部为0.1,则 x 1 x 1.0 y f )1( = (A)-1; (B)0.1; (C)1; (D)0.5. 3、(02,3 分)设函数 xf )( 在 R 上有界且可导,则 (A)当 (x 0) 时,必有 lim f 0)(lim x xf x lim f x 0)(lim ; (B)当 存在时,必有 x)( xf x ( 0 f 0)(lim0 ; (C) 当 lim x 0) 时,必有 x xf x (lim0 f x 0)(lim0 ; (D) 当 存在时,必有 x) xf x . 4、(03,4 分)已知 x x ln y 是微分方程 )( yx xy y 的解,则 )( yx 的表达式为 (A) . 2 2 x y (B) . 2 2 y x (C) . 2 2 y x (D) . 2 2 y x ( ) [ ] 5、(04,4 分)设函数 f x 连续, 且 f (0) 0 , 则存在 0 ( ) , 使得 (A) f x 在(0, ) 内单调增加. (B) f ( ) x 在( ,0 ) 内单调减小. (C)对任意的 x(0, ) 有 f ( ) (0 x f ) ( ,0 . (D)对任意的 x ) 有 f ( ) (0 x f ). n n n xf x 3 1lim)( ),( )1ln( ,2 2 ty ttx 6、(05,4 分)设函数 ,则 f(x)在 内 (A) 处处可导. (B) 恰有一个不可导点. (C) 恰有两个不可导点. (D) 至少有三个不可导点. [ ] 7、(05,4 分)设函数 y=y(x)由参数方程 确定,则曲线 y=y(x)在 x=3 处的法线与 x 轴交点的横坐标是 (A) 32ln 81 . (B) 32ln 8 32ln8 1 . (C) . (D) . [ ] 32ln8 8、 (06,4 分) 设函数 y fx ( ) 具有二阶导数,且 fx f x ( ) 0, ( ) 0 ,x 为 自变量 x 在 y 0 x 处的增量, 与 dy 分别为 f ( ) x 在点 0 x 处对应的增量与微 分,若 x 0,则 (A)0 dy y. 0 . y d y dy 0. (B) y (C) (D) dy y 0. [ ] 1 3

13、(10,4分)曲线y=x2与曲线y=alnx(a≠0)相切,则a= 9、(06.4分)设函数gx)可微,Mx)=e,h)=L,gD)=2,则g)等于 (A)4e (B)3e (C)2e (D)e (A)n3-1. (B)-n3-L. 二、填空题 (c)-ln2-l. (D)ln2-1. II 1.(01,3分)曲线e”-c0s(y)=e-1在点(0.1)处的切线方程为:. 10、(07,4分)设函数f(x)在x=0处连续,下列命题错误的是【1 2、(03,4分)设函数y=x)由方程灯y+2nx=y所确定,则曲线y=x)在点 人若g但在,则/0=0 (,)处的切线方程是 3.(05,4分)设y=(1+sinx)',则l,= B若回+/存在0=0 x 心4分》及y=由程y,则密。 c若但在在则f0=0 D--在f0=0 5.(07,4分)曲线c0s1+©0s1上对应于1=三的点处的法线斜率为 y=1+sint 4 x 1、(07,4分)设函数fx)在(0,+)上具有二阶导数,且f"(x)>0, 6、(07.4分)设函数y=2x中3·则广(0)=一 令4,=f)=L2,几,则下列结论正确的是 II 7、(08,4分)曲线sin(y)+n(y-x)=x在点(0,1)处的切线方程为 A若4>华,则{4}必收敛B.若4>山2,则{}必发散 C.若马<码,则{}必收敛D.若山<4,则{4}必发散 在(0,0)处的切线方程为。 12、(07,4分)二元函数f(x,y)在点(0,0)处可微的一个充分条件是[】 (y=rin(2-f 9、(09,4分)设y=x)是方程罗+'=x+1确定的隐函数,则 Am[fx小-f0,o]=0 Bf0-000,anf0000 10、(10·4分)函数y=1-2x)在x=0处的n阶号数 fs,0)-f0.0-0 C卿F+ y0)= 11,(10,4分)己知一个长方形的长I以2cm/s的速幸增加,宽w以3n/s的 D.m[f,(x0-f.0,0]=0,且1im[f,(x,0-f'0,0]=0 第2页共3页
第 页 共 页 1 ( e h g (1) 1, (1) 2 9、(06,4 分)设函数 可微, g x( ) h x( ) ) , g x g(1) ln 3 1 ln 3 1. ,则 等于 (A) . (B) (C) ln 2 1. (D)ln 2 1. [ ] 10、 (07,4 分) 设函数 f(x)在 x=0 处连续,下列命题错误的是 [ ] A. 若 0 ( ) lim x f x x 存在,则 f (0) 0 B. 若 0 lim x f () ( ) x fx f (0) 0 x 存在, C. 若 0 ( ) lim x f x x 存在, 则 f (0) 0 D. 0 lim x f () ( ) x fx f (0) 0 x 存在, 11、(07, 4 分)设函数 f ( ) x (0, f x "( ) 0 ) 1,2......., , 在 上具有二阶导数,且 ) , 令 = n u f (n n 则下列结论正确的是 [ ] A.若u1 u2 ,则un 1 必收敛 B. 若u u 2 ,则un u 必发散 C. 若u1 2 ,则 un 1 必收敛 D. 若u u 2 ,则un (, ) 必发散 12、(07,4 分) 二元函数 f x y , 0,0 0 y f 在点(0,0)处可微的一个充分条件是[ ] A. , 0,0 lim x y f x B. 0 ,0 0,0 0 f x lim x f x ,且 0 0, 0,0 lim 0 y f yf y C. 2 2 0,0 0 f x y , 0,0 ,0 lim x y f x D. 且 0 lim ' ,0 x x x f x f ' (0,0) 0, fx f ' ,0 ' (0,0) 0, y y 2 0 lim y 13、(10,4 分)曲线 y x 与曲线 y a xa ln ( 0) 相切,则 a __________ ( ) A 4e ( ) B 3e ( ) C 2e ( ) D e 1)cos( 2 e exy yx 二、填空题 1、(01,3 分)曲线 在点(0,1)处 的切线方程为 : 2、(03,4 分)设函数 y=f(x)由方程 所确定,则曲线 y=f(x)在点 (1,1)处的切线方程是 4 ln2 yxxy . 3、(05,4 分)设 ,则 x xy )sin1( dy |x =______ . 4、(06,4 分)设函数 y y x( ) 由方程 1 y y xe 确定,则 A 0 dydx = . 2 cos cos 1 sin x t t y t 5、(07,4 分)曲线 上对应于 4 t 的点处的法线斜率为_____ 6、(07,4 分)设函数 1 2 3 y x 0 n ,则 = y _____. 7、(08,4 分)曲线 sin ln xy yx x 在点 处的切线方程为 0,1 . 1 2 0 2 2 ln(2 ) t u x e du 8、(09,4 分)曲线 y t t ( ) 在(0,0)处的切线方程为____________ 1 y 9 、( 09 , 4 分)设 y y x 是方程 xye x 确定的隐函数,则 2 2 0 |x dydx =____________ 10 、( 10 , 4 分 )函数 y x ln(1 2 ) 在 x 0 处的 阶导数 n y (0) _____________ l 2 / cm s w 3 / cm s ( ) n 11、(10,4 分)已知一个长方形的长 以 的速率增加,宽 以 的 2 3

速率增加,则当1=12cm,1w=5cm时,它的对角线增加的速率为 6、(04,11分)某种飞机在机场降落时,为了减小滑行距离,在触地的瞬间,飞机 尾部张开减速伞,以增大阻力,使飞机迅速减速并停下来.现有一质量为 三、计算 9000g的飞机,着陆时的水平速度为700km/h.经测试,减速伞打开后,飞 1、(02,6分)已知曲线的极坐标方程为r=1-c0s0,求该曲线对应于日=:处的切 线与法线的直角坐标方程. 机所受的总阻力与飞机的速度成正比(比例系数为k=6.0×10).问从者陆 2、(02,7分),已知函数fx)在R上可导,fx)>0,1mfx)=1,且满足 点算起,飞机滑行的最长距离是多少注g表示千克.m/h表示千米/小 =. 时 7、(07,10分)已知函数f(a)具有二阶导数,且f0)=1,函数y=(x)由 x=1+22 3、(03,9分)设函数y与x)油参数方程 -三所商定求 方程-=1所定设:=-a尝装 8、(08,10分)曲线y=f(x)满足f(0)=1对于任意的1曲线是严格递增,在x 轴上1>0,该曲线与直线x=0,x=(1>0)及y=0用成一曲边梯形.该曲边 4、(03,10分)有一平底容器.其内侧壁是由曲线x=(y0y20)绕y轴旋转而成 梯形绕x轴旋转一周得一靛转体,其体积为V(),侧面积为St).如果f(x) 的旋转曲面(如图),容器的底面圈的半径为2m根据设计要求,当以3m/min 二阶可导且识=2,求曲线y=f). 的速幸向容器内注入液体时,液面的面积将以mm之/mn的速幸均匀扩大(假设 注入液体前,容器内无液体)。 (1)根据t时刻液面的面积,写出1与y)之间的关系式: 加分凌通产由s方产0-所商定:其中0 3 2)求曲线x=y)的方程(注:m表示长度单位米,min表示时间单位分) 具有2阶号数,且0=0=6,已知 云=40+求函数0. 5、(04,10分)设函数f(x)在(-0,+)上有定义,在区间0,2]上, f(x)=x-4),若对任意的x都满足f(x)=kf(x+2),其中k为常数. (I)写出f(x)在-2,0]上的表达式: ()问k为何值时,f(x)在x=0处可导 第3页共3页
6、(04,11分)某种飞机在机场降落时,为了减小滑行距离,在触地的瞬间,飞机 尾部张开减速伞,以增大阻力,使飞机迅速减速并停下来.现有一质量为 的飞机,着陆时的水平速度为 .经测试,减速伞打开后,飞 机所受的总阻力与飞机的速度成正比(比例系数为 ).问从着陆 点算起,飞机滑行的最长距离是多少 注 表示千克, 表示千米/小 时. 9000kg 700 / km h kg 6 k 6.0 10 km h/ 8、(08,10 分)曲线 y fx ( ) 满足 对于任意的 曲线是严格递增,在 f (0) 1 t x 轴上 ,该曲线与直线 t 0 x x 0, ) t t( 0 及 围成一曲边梯形.该曲边 梯形绕 y 0 x 轴旋转一周得一旋转体,其体积为V t( ) ,侧面积为 S t( ) .如果 f ( ) x 二阶可导,且 ( ) 2 9、(10,11 分)设函数 y f x( ) 由参数方程 所确定,其中 2 2 ,( 1) ( ) x tt t y t ( )t 具有 阶导数,且 2 5 (1) 2 第 3 页 共 3 页 速率增加,则当l cm w cm 12 , 5 时,它的对角线增加的速率为 ____________ 三、计算 1、(02, 6 分)已知曲线的极坐标方程为 r cos1 ,求该曲线对应于 6 处的切 线与法线的直角坐标方程. 2、(02,7 分). 已知函数 xf )( 在 R 上可导, , xf 0)( 1)(lim xf x ,且满足 h x e xf hxxf h 1 1 ) )( )( (lim0 ,求 .xf )( 3、(03, 9 分) 设函数 y=y(x)由参数方程 )1( ,21 ln21 1 2 t du ue y tx t u 所确定,求 . 9 2 2 x dx yd 4、(03, 10 分)有一平底容器,其内侧壁是由曲线 yyx )0)(( 绕 y 轴旋转而成 的旋转曲面(如图),容器的底面圆的半径为 2 m.根据设计要求,当以 min/3 3 m 的速率向容器内注入液体时,液面的面积将以 的速率均匀扩大(假设 min/ 2 m 注入液体前,容器内无液体). (1) 根据 t 时刻液面的面积,写出 t 与 y)( 之间的关系式; (2) 求曲线 yx )( 的方程.(注:m 表示长度单位米,min 表示时间单位分.) 5、(04, 10 分)设函数 f ( ) x 在( )上有定义 , , 在区间 上 [0, 2] , 2 f x xx ( ) ( 4) , 若对任意的 x 都满足 f x kf x ( ) ( 2) , 其中 为常数 k . (Ⅰ)写出 f ( ) x 在 上的表达式 [ 2, 0] ; (Ⅱ)问k 为何值时, f ( ) x 在 处可导 x 0 . 7、(07,10 分)已知函数 f ( ) a 具有二阶导数,且 =1,函数 由 方程 f '(0) y y ( ) x 1 1 y y xe 所确定.设 z f (ln sin ), y x 求 x 0 dzdx , 2 2 d z dx x0 . ( ) S t V t ,求曲线 y f x( ) . , (1) 6 ,已知 2 2 3 4(1 ) d y dx t ,求函数(t)