
第五章导数与微分 ·5.1导数的概念 ·5.2求导法则 ·5.3参变量函数的导数 ·5.4高阶导数 ·5.5微分
• 5.1 导数的概念 • 5.2 求导法则 • 5.3 参变量函数的导数 • 5.4 高阶导数 • 5.5 微分

5.1导数的概念 ·一、导数的定义 ·二、导函数 ·三、导数的几何意义
• 一、 导数的定义 • 二、 导函数 • 三 、导数的几何意义

一、问题的提出 ()瞬时速度问题 设一质点作直线运动,其运动规律为s=s(),若t为某一确 定时刻,为邻近于t的时刻,则质点在时间段[t,(或[6,)上 的平均速度为 p=s()-s(t) t-to 若t→t,时平均速度的极限存在,则称此极限 =lim s(t)-s(to) →to t-to 为质点在t时刻的瞬时速度
( ) ( ) . s t s t v t t 0 0 一、 问题的提出 (1) 瞬时速度问题 设一质点作直线运动,其运动规律为s=s(t),若t0为某一确 定时刻,t为邻近于t0的时刻,则质点在时间段[t0 ,t](或[t,t0 ])上 的平均速度为 若 t t 0 时平均速度的极限存在,则称此极限 ( ) ( ) lim t t s t s t v t t 0 0 0 为质点在t0时刻的瞬时速度
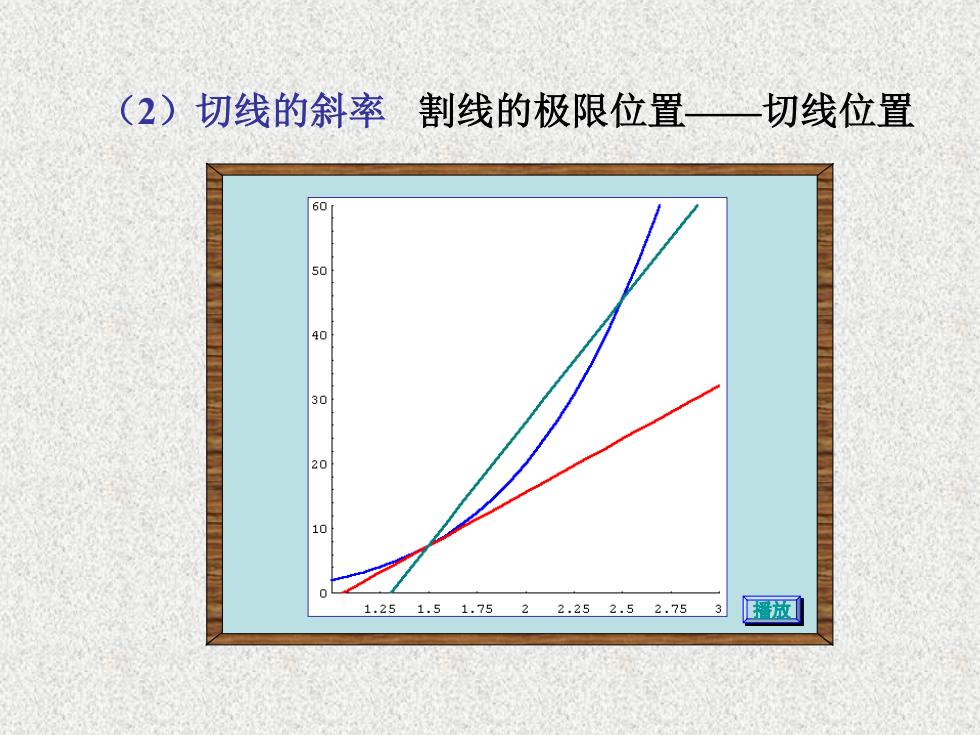
(2)切线的斜率割线的极限位置一切线位置 60 20 10 1.251.51.7522.252.52.753 播放
(2)切线的斜率 割线的极限位置——切线位置 播放
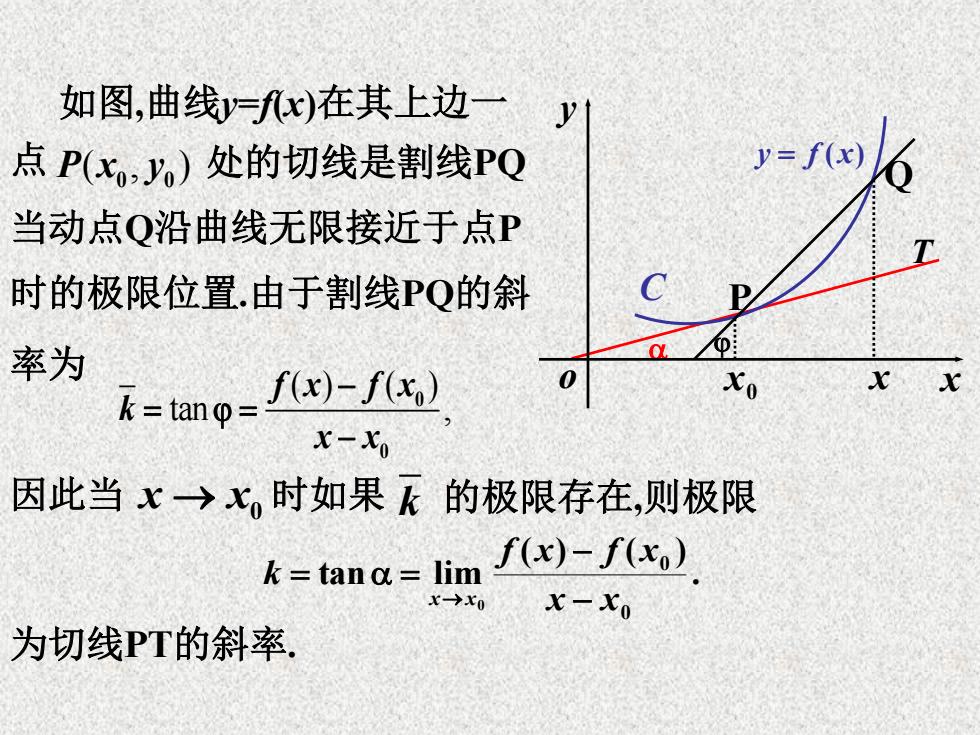
如图,曲线yx)在其上边一y1 点P(x,y)处的切线是割线PQ 6 y-J(w) 当动点Q沿曲线无限接近于点P 2 时的极限位置.由于割线PQ的斜 率为 K=tan=f(x)-f(G) x-xo 因此当x→x,时如果k的极限存在,则极限 k=tana=lim 、f(x)-f(xo) x→x0 x一xo 为切线PT的斜率
( ) ( ) tan , f x f x k x x 0 0 . ( ) ( ) tan lim 0 0 0 x x f x f x k x x 如图,曲线y=f(x)在其上边一 点 P x y ( , ) 0 0 处的切线是割线PQ T 0 o x x x y y f (x) C P Q 当动点Q沿曲线无限接近于点P 时的极限位置.由于割线PQ的斜 率为 因此当 x x 0 时如果 k 的极限存在,则极限 为切线PT的斜率

二、导数的定义 定义 设函数y=fx)在点x的邻域内有定义,若极限 lim f()-f(x) x→x0 x-xo 存在,则称函数f在点x可导,并称该极限为函数f在点x的 导数,记作f'(x),即 f(xo)=lim f(x)-f(x) x→x X-X0 若以上极限不存在,则称f在点x不可导
二、 导数的定义 ( ) ( ) ( ) lim . x x f x f x f x x x 0 0 0 0 定义 设函数y=f(x)在点x0的邻域内有定义,若极限 存在,则称函数f在点x0可导,并称该极限为函数f在点x0的 导数,记作 f x ( ), 0 即 ( ) ( ) lim . x x f x f x x x 0 0 0 若以上极限不存在,则称f在点x0不可导

如果令x=x,+△x,△y=f(x,+△x)-f(x), 则导数定义可为 f()=lim A lim f(x+△)-f(x) x→x0△比x→x0 △x 所以函数的导数是函数增量△y与自变量的增量△x之比 的极限,A儿称为函数关于自变量的平均变化率,而 △x △x fo)称为f在点x处关于x的变化率
( ) ( ) ( ) lim lim x x x x y f x x f x f x x x 0 0 0 0 0 如果令 x x x y f x x f x , ( ) ( ), 0 0 0 则导数定义可为 所以函数的导数是函数增量y与自变量的增量x之比 y x 的极限, y x 称为函数关于自变量的平均变化率,而 f'(x0 )称为f在点x0处关于x的变化率

三、导函数的几何意义 瞬时变化率是函数平均变化率的逼近函数. 100 为 % 25 -25 -50 -75 -100 播放
播放 三、导函数的几何意义 瞬时变化率是函数平均变化率的逼近函数

四、单侧导数 (1)左导数: 定义设函数fx)在x的左邻域xoδ,xl上有定义,若左 极限 lim f(e)-fn2-limf化+Ac)-fx】 △x→0 △x 存在,则称此极限为x)在x的左导数,记作f'(x)】
四、 单侧导数 (1)左导数: ( ) ( ) ( ) ( ) lim lim x x x f x f x f x x f x x x x 0 0 0 0 0 0 定义 设函数f(x)在x0的左邻域(x0 -,x0 ]上有定义,若左 极限 存在,则称此极限为f(x)在x0的左导数,记作 f x( ). 0

(2)右导数: 定义设函数fx)在x的右邻域xox+δ)上有定义,若右 极限 lim f)f()lim()-f() x→X0+ x-xo △x-→0+ △x 存在,则称此极限为fx)在x的右导数,记作f(x)
(2)右导数: ( ) ( ) ( ) ( ) lim lim x x x f x f x f x x f x x x x 0 0 0 0 0 0 定义 设函数f(x)在x0的右邻域[x0 ,x0 +)上有定义,若右 极限 存在,则称此极限为f(x)在x0的右导数,记作 f x( ). 0