
第三章函数极限 ·一、主要内容 ·1、函数极限的概念 ·2、函数极限的性质 ·3、函数极限存在的条件 ·4、两个重要的极限 ·5、无穷小量与无穷大量 前页 后页 返回
前页 后页 返回 第三章 函数极限 • 一、主要内容 • 1、函数极限的概念 • 2、函数极限的性质 • 3、函数极限存在的条件 • 4 、两个重要的极限 • 5 、无穷小量与无穷大量

二、目的要求 ·1、熟练掌握函数极限的定义,并能利用ε-δ语言对简单的 初等函数的极限给出证明: ·2、熟练掌握函数极限的性质并利用它对相关问题进行讨 论研究; ·3、掌握夹逼定理的基本思想; ·4、牢记两个重要极限的结果,会用两个重要极限作相关 的计算与证明: ·5、熟练掌握eine归结原理,并能利用leine定理对函数的 敛散性进行判断; ·5、掌握无穷小和无穷大的定义、性质和关系;能够对于 相对简单的无穷小及无穷大进行比较,了解阶的概念。 前页 后页 返回
前页 后页 返回 二、目的要求 • 1、 熟练掌握函数极限的定义,并能利用-语言对简单的 初等函数的极限给出证明; • 2、 熟练掌握函数极限的性质并利用它对相关问题进行讨 论研究; • 3、掌握夹逼定理的基本思想; • 4、 牢记两个重要极限的结果,会用两个重要极限作相关 的计算与证明; • 5、熟练掌握Heine归结原理,并能利用Heine定理对函数的 敛散性进行判断; • 5、掌握无穷小和无穷大的定义、性质和关系;能够对于 相对简单的无穷小及无穷大进行比较,了解阶的概念

·三、重点与难点 ·1、重点是函数极限的概念、性质 ·及计算。 ·2、难点是归结原理和柯西准则的 ·应用 前项 后页 返回
前页 后页 返回 • 三、重点与难点 • 1、重点是函数极限的概念、性质 • 及计算。 • 2、难点是归结原理和柯西准则的 • 应用

§1函数极限概念 在本章,我们将讨论函数极限的基本 概念和重要性质.作为数列极限的推广, 函数极限与数列极限之间有着密切的 联条,它们之间的纽带就是归结原理 一、x趋于0时的函数极限 二、X趋于X0时的函数极限 三、单侧极限 前顶 后页 返回
前页 后页 返回 §1 函数极限概念 一、x趋于时的函数极限 二、x趋于x0 时的函数极限 三、单侧极限 在本章,我们将讨论函数极限的基本 概念和重要性质.作为数列极限的推广, 函数极限与数列极限之间有着密切的 联系,它们之间的纽带就是归结原理. 返回

一、X趋于0时的函数极限 设函数f(x)定义在[a,+oo) 上,当x沿着x轴的正向A 无限远离原点时,函数f(x) f(x) 也无限地接近A,我们就称 f(x)当x趋于+o时以A为 极限 前页
前页 后页 返回 一、x趋于时的函数极限 设函数 f (x) 定义在 a, A f (x) x y O 极限. f (x)当 x 趋于 时以A为 也无限地接近A,我们就称 无限远离原点时,函数f (x) 上,当 x 沿着 x 轴的正向
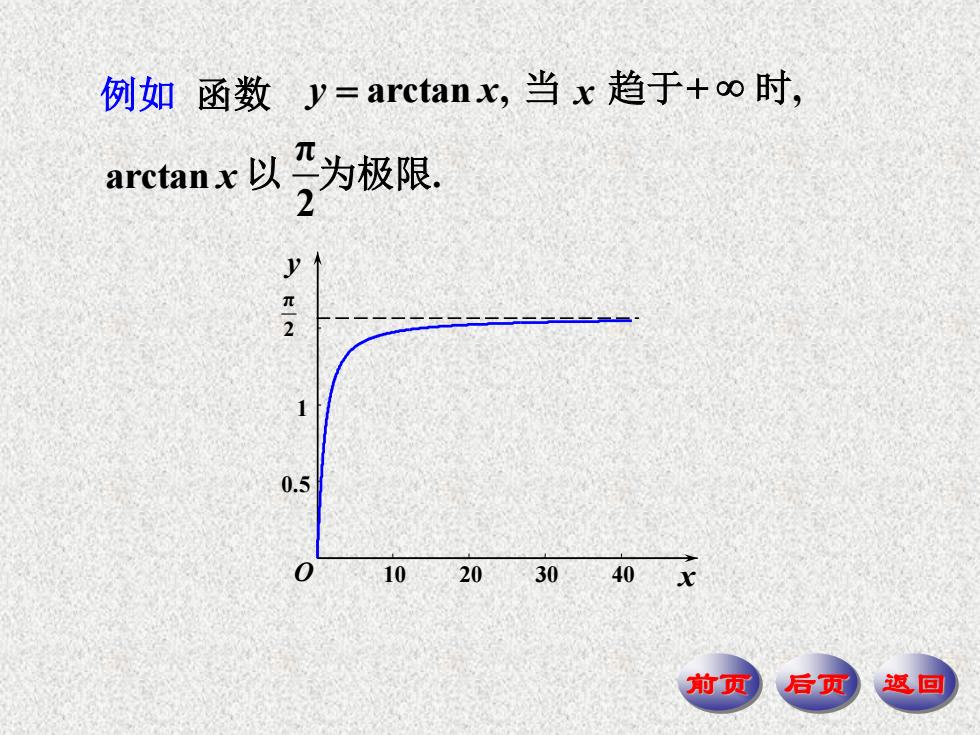
例如函数y=arctanx,当x趋于+oo时, arctanx以,为极限. 2 yT2 0.5 10 20 3040x 前顶 后页 返回
前页 后页 返回 例如 函数 y arctan x, 当 x 趋于 时, x y π 2 O 10 20 30 40 0.5 1 arctan x 以 为极限. π 2

定义1设f为定义在[a,+∞)上的一个函数.A为 定数,若对于任意正数s>0,存在M(≥),使得 当x>M时 f(x)-A<6, 则称函数f(x)当x趋于+∞时以A为极限, 记为 Iimf(x)=A或者f(x)→A(x-→+o). 前顶 后页 返回
前页 后页 返回 记为 lim ( ) 或者 x f x A f (x) A (x ). 定数, 若对于任意正数 0, 存在 M( a), 使得 f (x) A , 则称函数 f (x)当 x 趋于 时以 A为极限. 当x M 时, 定义1 设 f 为定义在a,上的一个函数. A 为
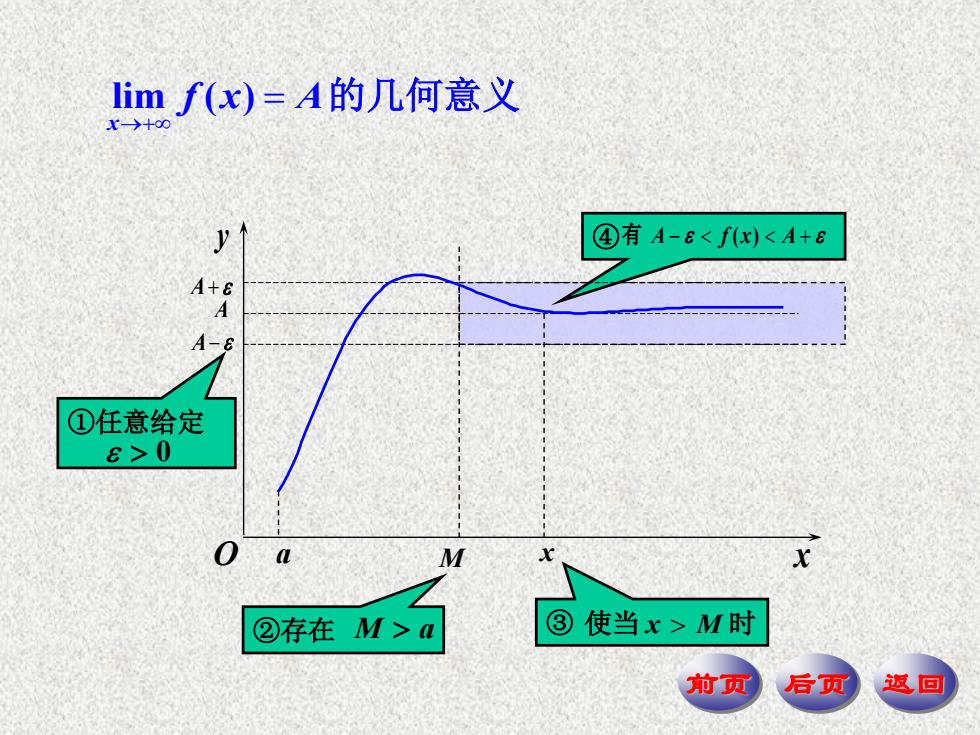
Iimf(x)=A的几何意义 →+00 y ④有A-60 O a ②存在M>a ③使当x>M时 前页 后页 返回
前页 后页 返回 ④ 有 A f x A ( ) lim ( ) x f x A 的几何意义 ③ 使当 x M 时 x A A ①任意给定 0 M ②存在 M a A x y O a
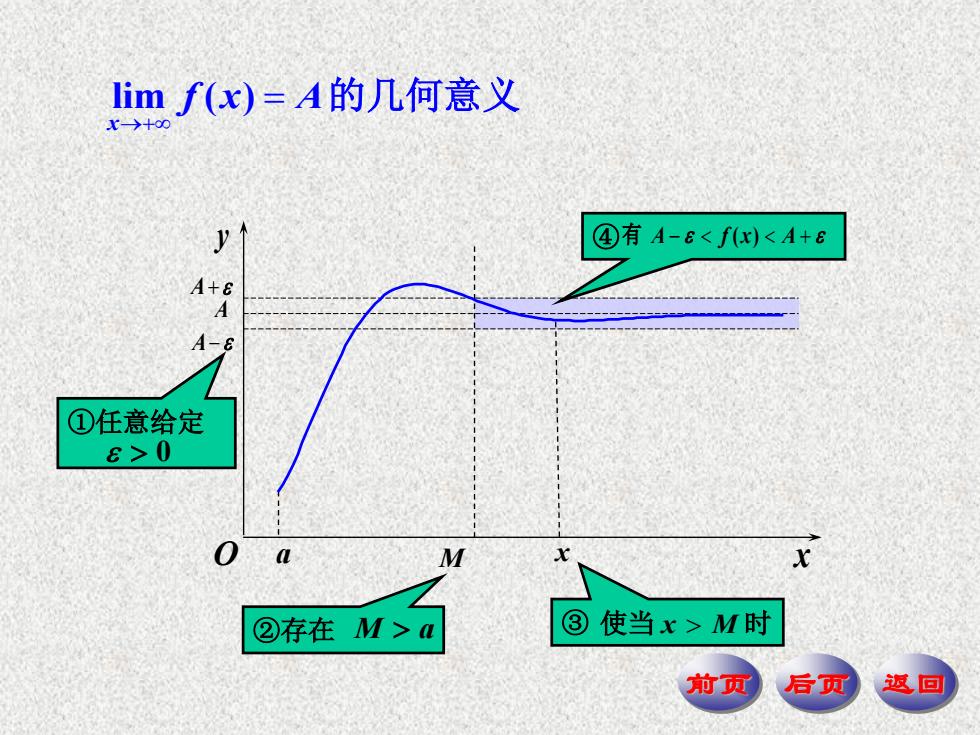
imf(x)=A的几何意义 +00 ④有A-G0 0 X ②存在M>a ③使当x>M时 前页 后页 返回
前页 后页 返回 ④ 有 A f x A ( ) lim ( ) x f x A 的几何意义 ③ 使当 x M 时 x A A ①任意给定 0 M ②存在 M a x A y O a

注数列可视为定义在正整数集上的函数.请大家 比较数列极限定义与函数极限定义之间的相同点 与不同点 例1证明1im1=0. x→+o0X 证任给e>0,取M=1,当x>M时, 8 fx)-0= <8 所以(由定义1), lim=0. x→+0X 前顶 后页 返回
前页 后页 返回 注 数列可视为定义在正整数集上的函数. 请大家 所以(由定义1), 例1 证明 0. 1 lim x x 证 任给 0, 取 , 1 M 当 x M 时, , 1 ( ) 0 x f x 0. 1 lim x x 与不同点. 比较数列极限定义与函数极限定义之间的相同点