
1.样本与抽样分布 理统计的基本概念 总体 在数理统计中,常把被考察对象的某一个(或多个)指标的全体称为总体 (或母体)。我们总是把总体看成一个具有分布的随机变量(或随机向量) 样本我们把从总体中抽取的部分样品x,x2,…,x称为样本。样本中所含的样 品数称为样本容量,一般用n表示。在一般情况下,总是把样本看成是n个相互 独立的且与总体有相同分布的随机变量,这样的样本称为简单随机样本。在泛指 任一次抽取的结果时,x,x2,x,表示n个随机变量(样本):在具体的一次抽 取之后,x,x2,,xn表示个具体的数值(样本值)。我们称之为样本的两重性。 样本函数和统计量 设x,x2,,xn为总体的一个样本,称 p=p(x1,x2,…,xn) 为样本函数,其中口为一个连续函数。如果口中不包含任何未知参数,则称p (x,2,…,xn)为一个统计量 常见统计量及其性质 样本均值 =x n 样本方差 S21、 x,-x n-1台 样本标准差 s=24- 样本k阶原点矩 M-空k=2 样本k阶中心矩 =2x-k=2 R-,- ES)=o2,ES*)=n-l
1.样本与抽样分布 数理统计的基本概念 总体 在数理统计中,常把被考察对象的某一个(或多个)指标的全体称为总体 (或母体)。我们总是把总体看成一个具有分布的随机变量(或随机向量) 样本 我们把从总体中抽取的部分样品 称为样本。样本中所含的样 品数称为样本容量,一般用 n 表示。在一般情况下,总是把样本看成是 n 个相互 独立的且与总体有相同分布的随机变量,这样的样本称为简单随机样本。在泛指 任一次抽取的结果时, 表示 n 个随机变量(样本);在具体的一次抽 取之后, 表示 n 个具体的数值(样本值)。我们称之为样本的两重性。 n ,,, xxx 21 L n ,,, xxx 21 L n ,,, xxx 21 L 样本函数和统计量 设 21 L,,, xxx n 为总体的一个样本,称 ϕ = ϕ ( 21 L,,, xxx n ) 为样本函数,其中ϕ 为一个连续函数。如果ϕ 中不包含任何未知参数,则称ϕ ( 21 L,,, xxx n )为一个统计量 常见统计量及其性质 . 1 1 ∑= = n i i x n 样本均值 x ∑= − − = n i i xx n S 1 2 2 .)( 1 1 样本方差 .)( 1 1 1 2 ∑= − − = n i i xx n 样本标准差 S 样本 k 阶原点矩 ∑= = = n i k k i kx n M 1 .,2,1, 1 L 样本 k 阶中心矩 ∑= ′ =−= n i k k i kxx n M 1 .,3,2,)( 1 L n XD 2 )( σ XE )( = μ , = , 2 1 2 )*( σ n n SE − = 22 SE )( = σ ,

其中S2-之(X,-x),为二阶中心矩 n (1)正态总体下的四大分布 正态分布 设x,x2,,xn为来自正态总体N(山,σ2)的一个样本,则样本函数 w女=华NO Gln t分布 设x,x2,…,x为来自正态总体N(,02)的一个样本,则样本函数 兰治- 其中t(血-1)表示自由度为n1的t分布 x2分布 设x,x2,,xn为来自正态总体N(4,σ)的一个样本,则样本函数 a--n 其中x2(n-1)表示自由度为n-1的x2分布。 F分布 设x,x2,,x为来自正态总体N(4,o)的一个样本,而,乃2,,y,为来自正态 总体N(4,o)的一个样本,则样本函数 Silai-F(-1.n-D). S31a3 其中 2-20- F(n1-1,n2-1)表示第一自由度为n,-1,第二自由度为n2-1的F分布。 (3)正态总体下分布的性质 X与S2独立
∑= = − n i i XX n S 1 2 2 )( 1 其中 * ,为二阶中心矩 (1) 正态总体下的四大分布 正态分布 设 为来自正态总体 的一个样本,则样本函数 ),( 2 21 L,,, xxx n N σμ ).1,0(~ / N n x u def σ − μ t 分布 设 为来自正态总体 的一个样本,则样本函数 ),( 2 21 L,,, xxx n N σμ ),1(~ / − − nt ns x t def μ 其中 t(n-1)表示自由度为 n-1 的 t 分布 χ2 分布 设 为来自正态总体 的一个样本,则样本函数 ),( 2 21 L,,, xxx n N σμ ),1(~ )1( 2 2 2 − − n Sn w def χ σ 其中 表示自由度为 n-1 的 分布。 )1( 2 χ n − 2 χ F 分布 设 为来自正态总体 的一个样本,而 为来自正态 总体 的一个样本,则样本函数 ),( 2 n N σμ 1 ,,, xxx 21 L n ,,, yyy 21 L ),( 2 N σμ 2 ),1,1(~ / / 2 21 2 2 2 2 1 2 1 nnF −− S S F def σ σ 其中 ,)( 1 1 2 1 1 2 1 1 ∑= − − = n i i xx n S ;)( 1 1 2 2 1 2 2 2 ∑= − − = n i i yy n S )1,1( nnF 21 −− 1 n1 − 1 表示第一自由度为 ,第二自由度为n2 − 的 F 分布。 (3)正态总体下分布的性质 X 与 独立。 2 S

2.参数估计 (1)点矩估计 估计 设总体X的分布中包含有未知数日1,02,…,日,则其分布函数可以表成 F(x:01,02,…,0)它的k阶原点矩y=E(Xk=1,2,…,m)中也 包含了未知参数日,02,…,0n,即y1=y(旧1,02,…,日n)。又设 x,x2,…,x为总体X的n个样本值,其样本的k阶原点矩为 空女=2叫 这样,我们按照“当参数等于其估计量时,总体矩等于相应的样本矩 的原则建立方程,即有 4…)2 ,84…,6n)=2, 4… k成成2x 由上面的m个方程中,解出的m个未知参数(0,02,…,0)即为参数 (8,82,…,8m)的矩估计量。 若0为0的矩估计,g(x)为连续函数,则g(⊙为g()的矩估计
2.参数估计 (1)点 估计 矩估计 设总体 X 的分布中包含有未知数θ θ θ m ,,, 21 L ,则其分布函数可以表成 ).,,,;( 21 m xF θ θ L θ 它的 k 阶原点矩 中也 包含了未知参数 kXEv m),,2,1)(( k k = = L ),,,( kk 21 m θ θ 21 L,,, θ m , 即 = vv θ θ L θ 。又设 为总体 X 的 n 个样本值,其样本的 k 阶原点矩为 n ,,, xxx 21 L ∑= n i k i x n 1 1 k = L m).,,2,1( 这样,我们按照“当参数等于其估计量时,总体矩等于相应的样本矩” 的原则建立方程,即有 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ = = = ∑ ∑ ∑ = ∧∧ ∧ = ∧∧ ∧ = ∧∧ ∧ n i m m m i n i m i n i m i x n v x n v x n v 1 21 1 2 212 1 211 . 1 ),,,( , 1 ),,,( , 1 ),,,( θθθ θθθ θθθ L LLLLLLLLL L L 由上面的 m 个方程中,解出的 m 个未知参数 即为参数 ( ),,,( 21 ∧∧ ∧ L θθθ m θ θ θ m ,,, 21 L )的矩估计量。 若 为 ∧ θ θ 的矩估计, 为连续函数,则 为)ˆ xg )( g(θ g θ )( 的矩估计

极大似 当总体X为连续型随机变量时,设其分布密度为 然估计 f(x0,0,…,0n),其中0,0,…,0n为未知参数。又设 x1,x2,…,xn为总体的一个样本,称 L(8,0,…,0)=fx8,0,…,0) 为样本的似然函数,简记为 当总体X为离型随机变量时,设其分布律为 PX=x}=px01,0,…,0n),则称 L,,x8,0.,,0.)=px8,0…,0) 为样本的似然函数。 若似然函数L(x,x,…,xn:0,0,…,0)在01,0:,…,0m处 到最大值,则称日1,8:,…,0m分别为日,0,…,0n的最大似然估计值 相应的统计量称为最大似然估计量。 alnL, 80.le-5. 0,i=1,2,…,m 若日为0的极大似然估计,g(x)为单调函数,则g(为g()的极大 似然估计。 (2)估无偏性 计量的 设0=0(x,x2,…,n)为未知参数0的估计量。若E(0)=0,则称 评选标 日为的无偏估计量。 E (=E (X),E (S)=D (X) 有效性 设日1=日1(x1,x2,…,x.)和0:=02(x1,x2,…,x)是末知参数0 的两个无偏估计量。若D(1)<D02),则称1比02有效
极大似 然估计 当总体 X 为连续型随机变量时,设其分布密度为 ,其中 为未知参数。又设 为总体的一个样本,称 2 ),,,;( 1 m xf L θθθ θθθ m 2 ,,, 1 L n 2 ,,, xxx1 L ),,,;(),,,( 1 1 2 ∏ 1 2 = = n i m i m L L θθθ xf L θθθ 为样本的似然函数,简记为Ln. 当总体 X 为离型随机变量时,设其分布律为 2 ),,,;(}{ ,则称 1 m == xpxXP L θθθ ),,,;(),,,;,,,( 1 1 2 1 2 ∏ 1 2 = = n i n m i m L xxxL L θθθ xp L θθθ 为样本的似然函数。 若似然函数 2 2 ),,,;,,,( 1 n 1 m L xxxL θ θ L θ 在 处取 到最大值,则称 分别为 m ∧∧ ∧ 1 2 L,,, θθθ m ∧∧ ∧ 1 2 L,,, θθθ θ θ θ m 2 ,,, 1 L 的最大似然估计值, 相应的统计量称为最大似然估计量。 mi L i i i n ,,2,1,0 ln == L ∂ ∂ ∧ =θθ θ 若 为 ∧ θ θ 的极大似然估计, 为单调函数,则 为)ˆ xg )( g(θ g θ )( 的极大 似然估计。 无偏性 设 为未知参数 的估计量。若 E ( )= ,则称 为 的无偏估计量。 ),,,( 21 n L xxx ∧∧ =θθ θ ∧ θ θ ∧ θ θ E( X )=E(X), E(S2 )=D(X) (2)估 计量的 评选标 准 有效性 设 和 是未知参数 的两个无偏估计量。若 ,则称 有效。 ),,,,( 21 11 n L xxx ∧∧ =θθ ),,,,( 21 22 n L xxx ∧∧ =θθ θ 1 2 )()( ∧ ∧ < DD θθ 21 ∧∧ 比θθ
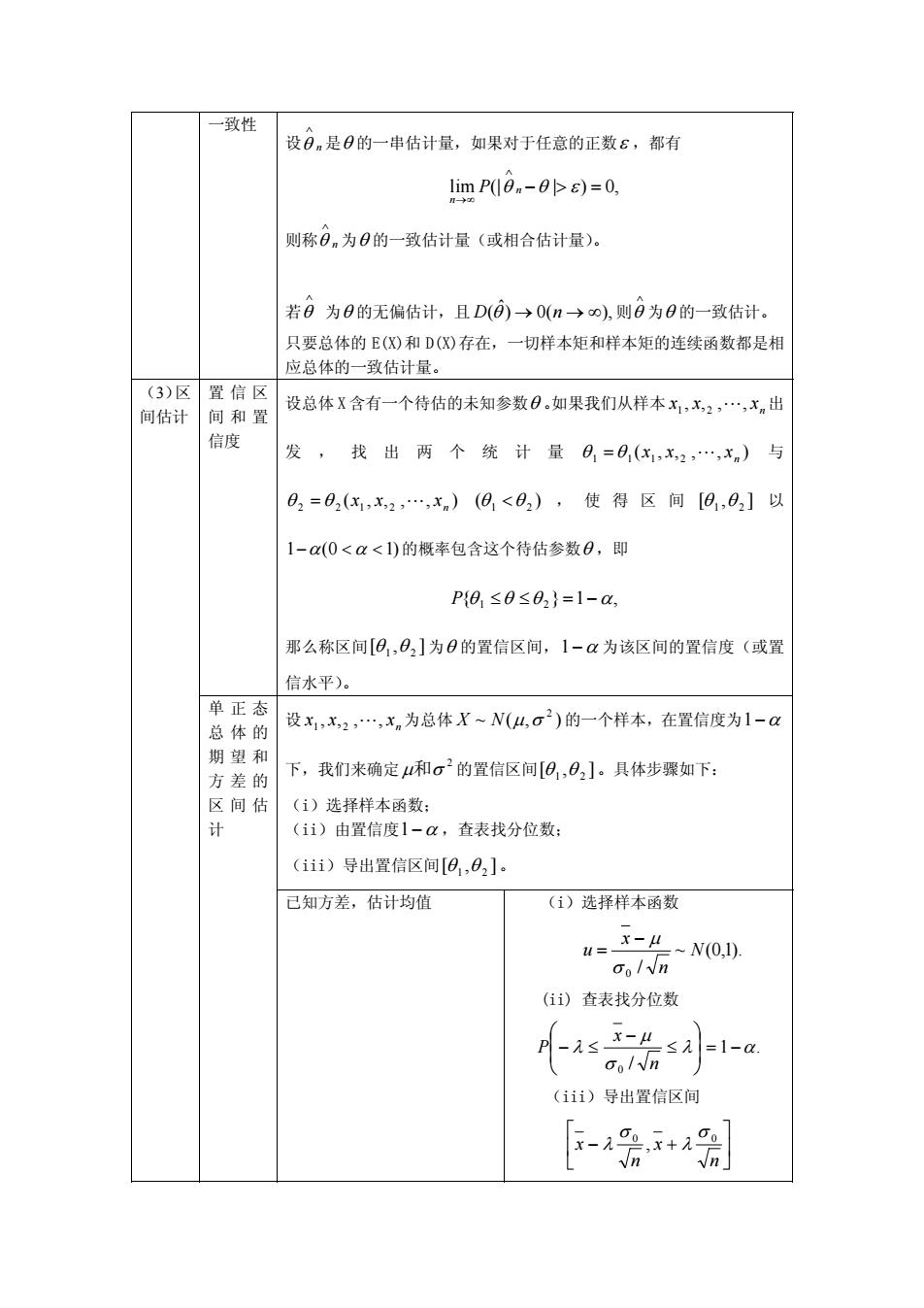
致性 设0n是B的一串估计量,如果对于任意的正数£,都有 limP0,-0s)=0, 则称0,为0的一致估计量(或相合估计量) 若日为B的无偏估计,且D(©→0(n→0),则日为日的一致估计. 只要总体的E(风)和D()存在,一切样本矩和样本矩的连续函数都是相 应总体的一致估计量。 (3)区置信区 间估计 间和置 设总体X含有一个待估的未知参数日,如果我们从样本x,x2,…,x,出 信 发, 找出两个统计量日=0,(x,x2,…,x,)与 02=02(x,x2,…,xn)(0<02),使得区间[日1,02]以 1-a(0<<1)的概率包含这个待估参数,即 P{8≤0≤02}=1-a, 那么称区间[日,02]为0的置信区间,1-a为该区间的置信度(或置 信水平)。 单正态 总体的 设x1x,2,…,xn为总体X~N(4,o)的一个样本,在置信度为1-a 期望和 方差的 下,我们来确定4和σ2的置信区间[旧,02]。具体步骤如下: 间估 (1)选择样本函数: 计 (ii)由置信度1-a,查表找分位数: (iii)导出置信区间[0,0]. 己已知方差,估计均值 (i)选择样本函数 =--N(0.1) Goln (ii)查表找分位数 (iii)导出置信区间 -会+
一致性 设 是n ∧ θ θ 的一串估计量,如果对于任意的正数ε ,都有 =>− ,0)|(|lim ∧ ∞→ n εθθ n P 则称 为n ∧ θ θ 的一致估计量(或相合估计量)。 若 为 ∧ θ θ 的无偏估计,且 则 为 ∧ ),(0) θ ˆ (θ nD ∞→→ θ 的一致估计。 只要总体的 E(X)和 D(X)存在,一切样本矩和样本矩的连续函数都是相 应总体的一致估计量。 置信区 间和置 信度 设总体 X 含有一个待估的未知参数θ 。如果我们从样本 出 发,找出两个统计量 n ,,,, xxx 21 L ),,,,( 2111 n θ =θ L xxx 与 ),,,,( 2122 n θ =θ L xxx )(θ <θ 21 ,使得区间 ],[θ θ 21 以 α α <<− )10(1 的概率包含这个待估参数θ ,即 { ,1} P θ 1 ≤θ ≤θ 2 = −α 那么称区间 ],[θ θ 21 为θ 的置信区间,1−α 为该区间的置信度(或置 信水平)。 (3)区 间估计 设 21 L,,,, xxx n 为总体 ),(~ 的一个样本,在置信度为 2 NX σμ 1−α 下,我们来确定 的置信区间 2 和σμ ],[θ θ 21 。具体步骤如下: (i)选择样本函数; (ii)由置信度1−α ,查表找分位数; (iii)导出置信区间 ],[θ θ 21 。 单正态 总体的 期望和 方差的 区间估 计 已知方差,估计均值 (i)选择样本函数 ).1,0(~ / 0 N n x u σ − μ = (ii) 查表找分位数 .1 / 0 αλ σ μ λ −=⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ≤ − ≤− n x P (iii)导出置信区间 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +− n x n x 0 0 , σ λ σ λ

未知方差,估计均值 (i)选择样本函数 (ii)查表找分位数 小a (iii)导出置信区间 方差的区间估计 (i)选择样木函数 w=a-S2ea-》 元2 (ii)查表找分位数 is(-Dss--a (iii)导出o的置信区间 [受受 3.假设检验 基本思想 假设检验的统计思想是,概率很小的事件在一次试验中可以认为基本上是不 会发生的,即小概率原理。 为了检验一个假设居是否成立。我们先假定是成立的。如果根据这个假定 导致了一个不合理的事件发生,那就表明原来的假定是不正确的,我们拒绝接 受:如果由此没有导出不合理的现象,则不能拒绝接受品,我们称是相容的。 与B相对的假设称为备择假设,用表示。 这里所说的小概率事件就是事件{K∈R},其概率就是检验水平a,通常我 们取a=0.05,有时也取0.01或0.10。 基本步骤 假设检验的基本步骤如下 (i) 提出零假设:
未知方差,估计均值 (i)选择样本函数 ).1(~ / − − = nt nS x t μ (ii)查表找分位数 .1 / αλ μ λ −=⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ≤ − ≤− nS x P (iii)导出置信区间 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ +− n S x n S x , λλ 方差的区间估计 (i)选择样本函数 ).1(~ )1( 2 2 2 − − = n Sn w κ σ (ii)查表找分位数 .1 )1( 2 2 2 1 αλ σ λ −=⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ≤ − ≤ Sn P (iii)导出σ 的置信区间 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −− S n S n 2 1 1 , 1 λλ 3.假设检验 基本思想 假设检验的统计思想是,概率很小的事件在一次试验中可以认为基本上是不 会发生的,即小概率原理。 为了检验一个假设H0是否成立。我们先假定H0是成立的。如果根据这个假定 导致了一个不合理的事件发生,那就表明原来的假定H0是不正确的,我们拒绝接 受H0;如果由此没有导出不合理的现象,则不能拒绝接受H0,我们称H0是相容的。 与H0相对的假设称为备择假设,用H1表示。 }{ 这里所说的小概率事件就是事件 ∈ RK α ,其概率就是检验水平α,通常我 们取α=0.05,有时也取 0.01 或 0.10。 基本步骤 假设检验的基本步骤如下: (i) 提出零假设H0;

(ii)选择统计量k (iii)对于检验水平a查表找分位数x: (i)由样本值x,x2,…,x,计算统计量之值: 将及与进行比较,作出判断:当1衣卜(或R>)时否定品,否则认为相容。 两类错误 第一类错误 当为真时,而样本值却落入了否定域,按照我们规定的检验法则,应当否定%。 这时,我们把客观上成立判为为不成立(即否定了真实的假设),称这种错误 为“以真当假”的错误或第一类错误,记α为犯此类错误的概率,即 P{否定B为真}=a: 此处的α恰好为检验水平。 第二类错误 当H为真时,而样本值却落入了相容域,按照我们规定的检验法则,应当接受。 这时,我们把客观上弘。不成立判为成立(即接受了不真实的假设),称这种错 误为“以假当真”的错误或第二类错误,记B为犯此类错误的概率,即 P{接受H为真]=B。 两类错误的关系 人们当然希望犯两类错误的概率同时都很小。但是,当容量一定时,α变 小,则B变大:相反地,B变小,则a变大。取定α要想使B变小,则必须增加 样本容量。 在实际使用时,通常人们只能控制犯第一类错误的概率,即给定显著性水平α。 ā大小的选取应根据实际情况而定。当我们宁可“以假为真”、而不愿“以真当 假”时,则应把a取得很小,如0.01,甚至0.001。反之,则应把ā取得大些。 单正态总体均值和方差的假设检验 条件 零假设 统计量 对应样本 否定域 函数分相 已知o2 H。=4 N(0,1) p号 U=
(ii) 选择统计量 K; (iii) 对于检验水平α查表找分位数λ; (iv) 由样本值 21 L,,, xxx n 计算统计量之值 K; 将 进行比较,作出判断:当 与λ 时否定H ∧ K >> λλ )(|| ∧ ∧ 或 KK 0,否则认为H0相容。 两类错误 第一类错误 当H0为真时,而样本值却落入了否定域,按照我们规定的检验法则,应当否定H0。 这时,我们把客观上H0成立判为H0为不成立(即否定了真实的假设),称这种错误 为“以真当假”的错误或第一类错误,记α 为犯此类错误的概率,即 P{否定H0|H0为真}=α ; 此处的α恰好为检验水平。 第二类错误 当H1为真时,而样本值却落入了相容域,按照我们规定的检验法则,应当接受H0。 这时,我们把客观上H0。不成立判为H0成立(即接受了不真实的假设),称这种错 误为“以假当真”的错误或第二类错误,记 β 为犯此类错误的概率,即 P{接受H0|H1为真}= β 。 两类错误的关系 人们当然希望犯两类错误的概率同时都很小。但是,当容量 n 一定时,α 变 小,则 β 变大;相反地,β 变小,则α 变大。取定α 要想使 β 变小,则必须增加 样本容量。 在实际使用时,通常人们只能控制犯第一类错误的概率,即给定显著性水平α。 α大小的选取应根据实际情况而定。当我们宁可“以假为真”、而不愿“以真当 假”时,则应把α取得很小,如 0.01,甚至 0.001。反之,则应把α取得大些。 单正态总体均值和方差的假设检验 对应样本 条件 零假设 统计量 否定域 函数分布 2 1 || α − > uu 0 0 已知 σ2 H : μ = μ N(0,1) x U / − μ 0 =
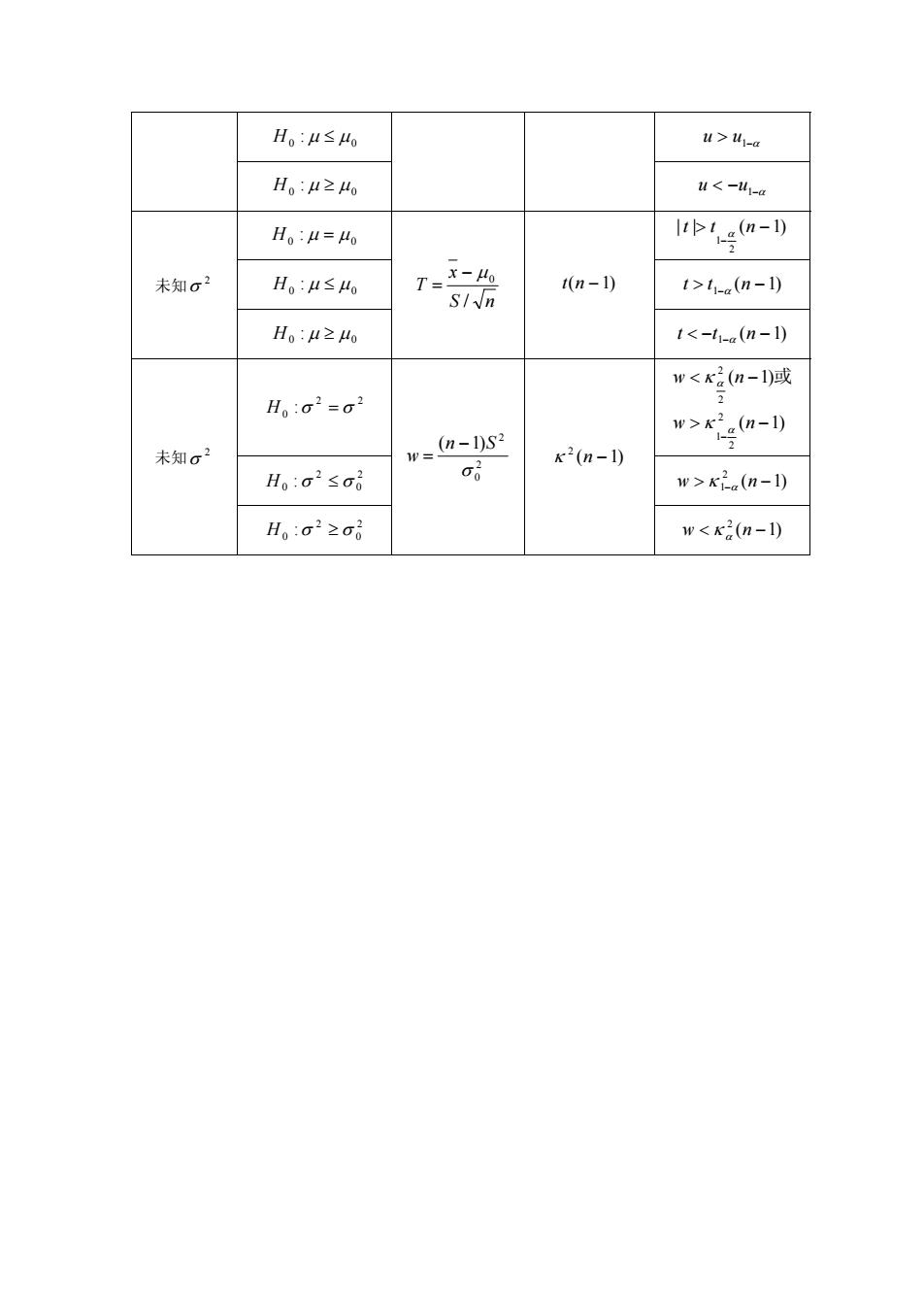
H0:u≤ u>u-a H。:4≥4o u1-(n-1) S/√n Ho:μ≥o tKa(n-1) 未知o2 (n-1)S2 68 K2(n-1) H:o2≤o6 w>kig(n-1) H。:o2≥o w<x2(n-1)
0 0 H : μ ≤ μ > uu 1−α 0 0 H : μ ≥ μ − − ntt α 0 0 H : μ = μ 0 0 H : μ ≤ μ )1( 未知 1−α ntt −> 2 σ 0 0 H : μ ≥ μ nS T / 0 = )1( x − μ nt − )1( 1−α ntt −− − 未知 2 σ 2 0 2 0 H : ≥ σσ 2 0 2 )1( σ Sn w − = )1( 2 κ n − )1( 2 κ α nw −<