
第六章微分中值定理及应用 ·6.1拉格郎日定理和函数的单调性 ·6.2柯西中值定理和不定式极限 ·6.3泰勒公式 ·6.4函数的极值与最大最小值 ·6.5函数的凸性和拐点 ·6.6函数图像的讨论
• 6.1 拉格郎日定理和函数的单调性 • 6.2 柯西中值定理和不定式极限 • 6.3 泰勒公式 • 6.4 函数的极值与最大最小值 • 6.5 函数的凸性和拐点 • 6.6 函数图像的讨论

6.1拉格朗日定理和☒数的单调性 ·一、罗尔定理 ·二、拉格郎日定理 ·三、单调函数
• 一、罗尔定理 • 二、拉格郎日定理 • 三、单调函数

微分中值定理的核心是拉格朗日(Lagrange) 中值定理,费马定理是它的预备定理,罗尔定理 是它的特例,柯西定理是它的推广。 一、预备定理 费马Fermat)定理 若函数fx)在(a,b)内一点x取得极值,且fx)在x可微,则 f'(x)=0. 费马(Fermat,1601-1665),法国人, 与笛卡尔共同创立解析几何。因提出费马 大、小定理而著名
微分中值定理的核心是拉格朗日(Lagrange) 中值定理,费马定理是它的预备定理,罗尔定理 是它的特例,柯西定理是它的推广。 一、预备定理——费马(Fermat)定理 费马(Fermat,1601-1665),法国人, 与笛卡尔共同创立解析几何。因提出费马 大、小定理而著名。 ( ) 0. 0 f x = 若函数f(x)在(a,b)内一点x0取得极值,且f(x)在x0可微,则
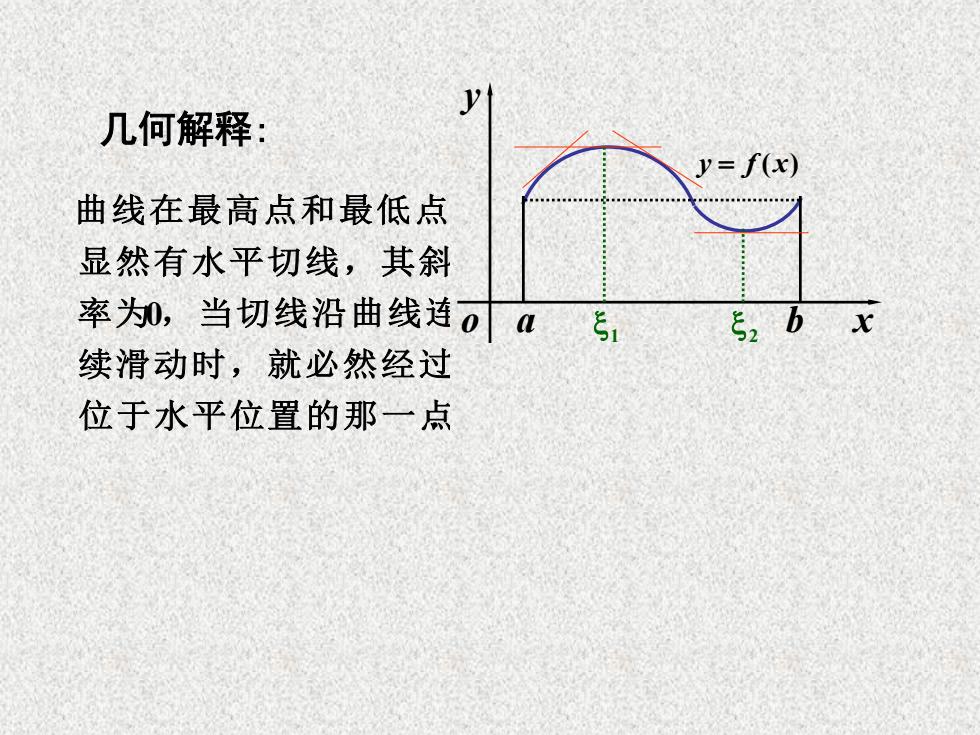
y 几何解释: y=f(x) 曲线在最高点和最低点 显然有水平切线,其斜 率为0,当切线沿曲线连oa E2b x 续滑动时,就必然经过 位于水平位置的那一点
x y o y = f (x) a b 1 2 几何解释: . 0 位于水平位置的那一点 续滑动时,就必然经过 率 为 ,当切线沿曲线连 显然有水平切线,其斜 曲线在最高点和最低点

证明:只就fx)在x取极大值的情形给出证明。 由于fx)在x取极大值,所以存在δ>0,当x∈Uc,δ)时,有 fx)sfx),又fx)在x可导,所以f'(x)=f(x)=f'(x) 而 fx)=1mf)-fs0, x-→x0+ x-xo f(xo)=lim f(x)-fx≥0, x-xo-X-o 所以f'(x)=0:
证明: 只就f(x)在x0取极大值的情形给出证明. 由于f(x)在x0取极大值,所以存在>0,当xU(x0 , )时,有 f(x) f(x0 ),又f(x)在x0可导,所以 而 ( ) ( ) ( ) lim , x x f x f x f x x x = 0 0 0 0 0 ( ) ( ) ( ) lim , x x f x f x f x x x = 0 0 0 0 0 所以 f x f x f x ( ) ( ) ( ). 0 0 0 = = 所以 f x ( ) . 0 = 0
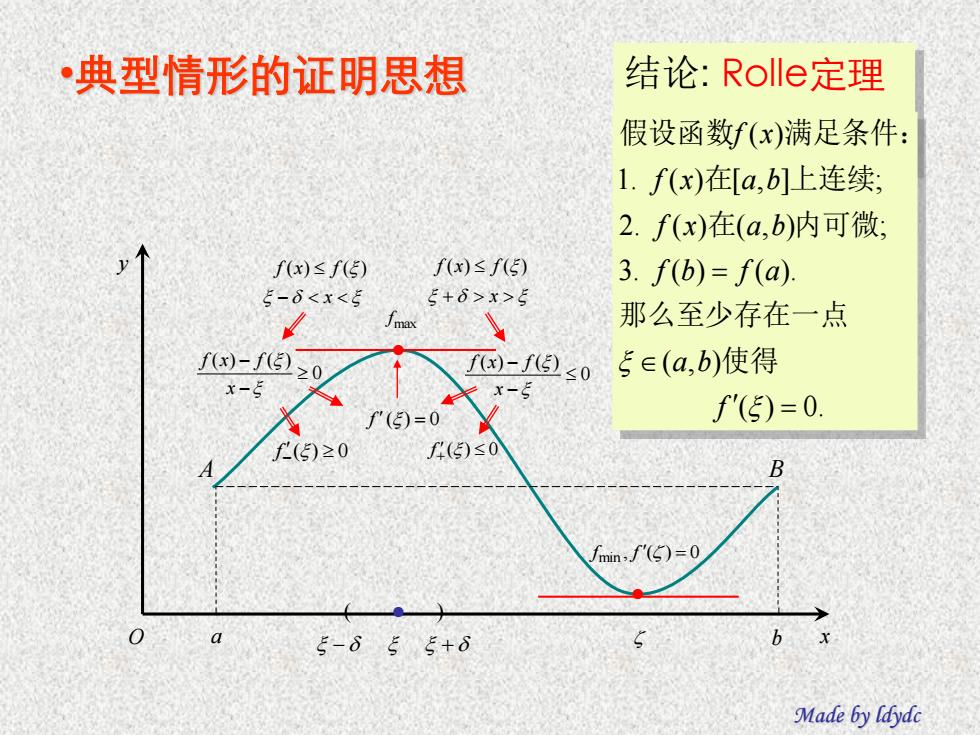
•典型情形的证明思想 结论:Rolle定理 假设函数f(x)满足条件: 1.f(x)在[a,b]上连续; 2.f(x)在(a,b)内可微: fx)≤f(5) f(x)≤f(5) 3.f(b)=f(a) 5-6x>5 /max 那么至少存在一点 fw)-f且20 f)-f≤0 5∈(a,b)使得 x-5 x-9 ()=0 '(5)=0. (5)≥0 f(5)≤0 B fmn,f'(ξ)=0 0 5-δ55+6 b Made by ldydc
O a b x y A B ● ● max f fmin , f ( ) = 0 x f (x) f ( ) f () = 0 ( ) 0 f () 0 f x f (x) f ( ) ( ) 0 ( ) ( ) x f x f 0 ( ) ( ) x f x f 这说明:在极 大值或极小值 点处,函数的导 数为0. 几何意义是: 在极值点处的 切线平行于AB 的连线或x轴. •典型情形的证明思想 ● 结论: Rolle定理 ( ) 0. ( , ) 3. ( ) ( ). 2. ( ) ( , ) ; 1. ( ) [ , ] ; ( ) = = f a b f b f a f x a b f x a b f x 使得 那么至少存在一点 在 内可微 在 上连续 假设函数 满足条件: Made by ldydc

二、Rolle定理 l.Rolle定理 定理2(RoIIe定理)如果函数f(在闭区间[a,b] 上连续,在开区间(a,b)内可导,3且在区间端点的函数 值相等,即f()=f(b),那末在(a,b)内至少有一点 (M≤飞<b),使得函数f(x)在该点的导数等于零, 即f(飞)=0 "罗尔:法国数学家,1652年4月21日生于昂贝尔特, ”罗尔在数学上的成就主要是在代数方面,专长于丢 番图方程的研究
二、Rolle定理 定理 2 (Rolle 定理) 如果函数 f (x)在闭区间 [a,b] 上连续,在开区间(a,b)内可导,且在区间端点的函数 值相等,即 f (a) = f (b),那末在(a,b)内至少有一点 (a b),使得函数 f (x)在该点的导数等于零, 即 ( ) 0 ' f = (1) (2) (3) 1.Rolle定理 罗尔:法国数学家,1652年4月21日生于昂贝尔特, 罗尔在数学上的成就主要是在代数方面,专长于丢 番图方程的研究

证因为fx)在a,b]上连续,所以必取得最大值M和最 小值m. (I)若M=m,则fx)=M,由此得fx)=0,所以∈(a,b), 都有f'(5)=0 (2)若M≠m,由于fa)=fb),所以函数的最大值和最小 值不可能同时在端点取得,不妨设Mfa),则在(a,b)内至 少存在一点ξ,使M=f飞),因为f(5+△x)≤f(),所以 f(5+△x)-f(5)≤0
证 (a,b), f x f ( ) ( ), f x f ( ) ( ) , 0 (1)若M=m,则f(x) M,由此得f'(x)0,所以 因为f(x)在[a,b]上连续,所以必取得最大值M和最 小值m. 都有 f ( ) . = 0 (2)若Mm,由于f(a)=f(b),所以函数的最大值和最小 值不可能同时在端点取得,不妨设M f(a),则在(a,b)内至 少存在一点,使M =f(),因为 所以
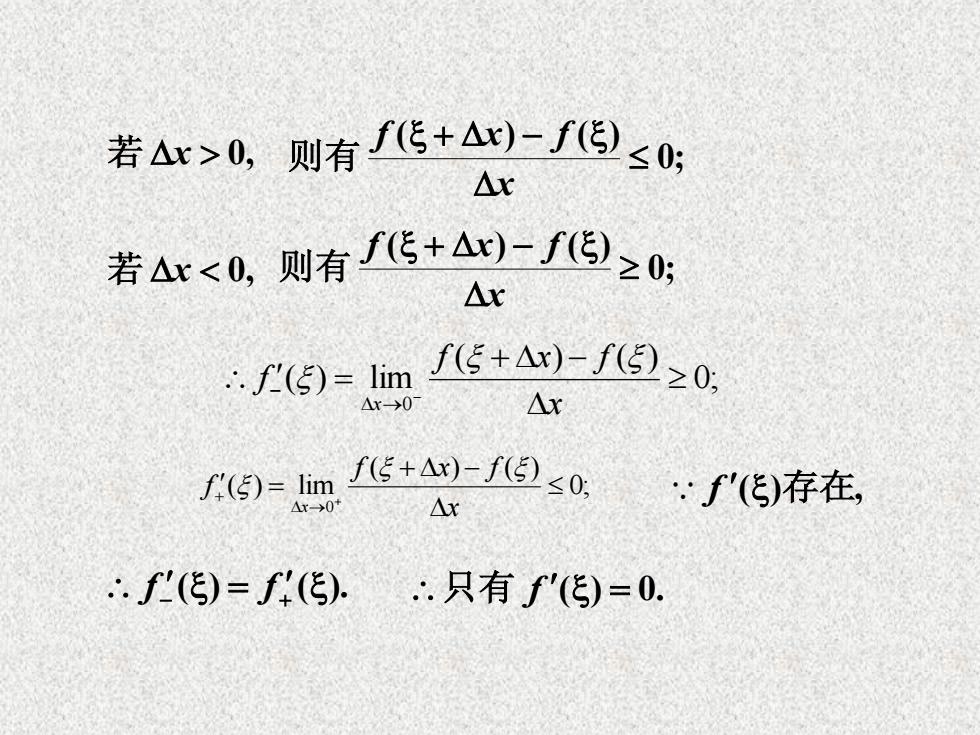
若△x>0,则有f5+A)-f5)s0: △x 若Ar0 △x f6)= f5+A,)-f⑨s0, f'(传)存在, Ar ∴f'(传)=f(传)..只有f'(传)=0
若 x 0, 0; ( ) ( ) x f x f 则有 若 x 0, 0; ( ) ( ) x f x f 则有 0; ( ) ( ) ( ) lim 0 = x f x f f x 0; ( ) ( ) ( ) lim 0 = x f x f f x f ()存在, () = (). f f 只有 f () = 0
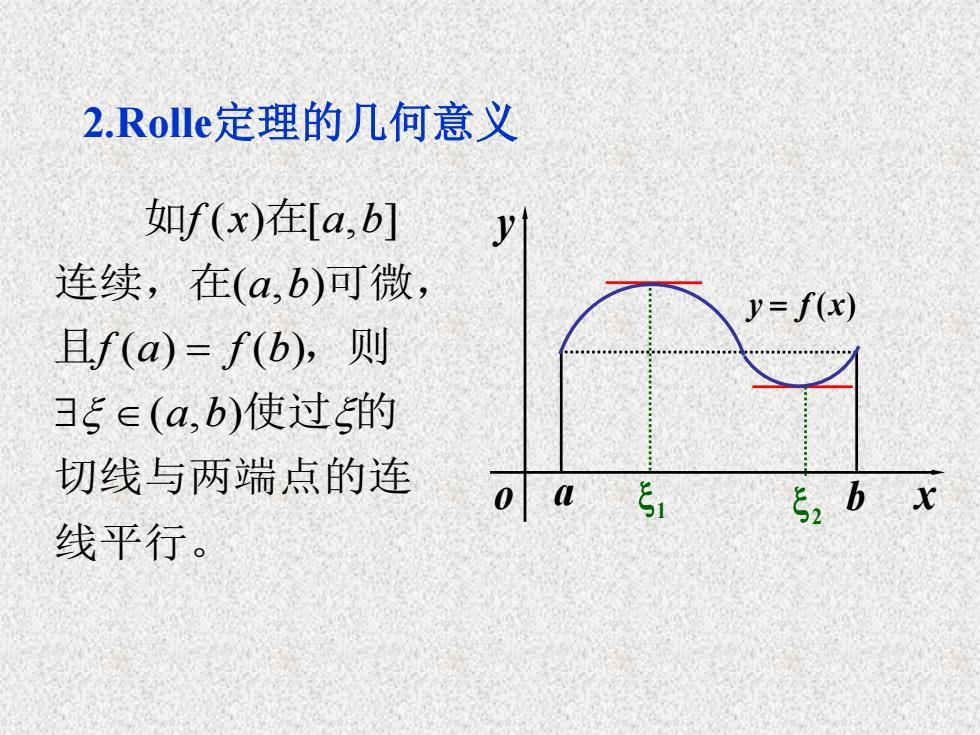
2.Rolle定理的几何意义 如f(x)在[a,b] y 连续,在(a,b)可微, y=f(x) 且f(a)=f(b),则 35∈(a,b)使过的 切线与两端点的连 051 52bx 线平行
2.Rolle定理的几何意义 a 1 b 2 x y o y = f (x) 线平行。 切线与两端点的连 使过 的 且 ,则 连续,在 可微, 如 在 ( , ) ( ) ( ) ( , ) ( ) [ , ] a b f a f b a b f x a b =