
第十一章反常积分 11.1反常积分概念 11.2无穷积分的性质与收敛判别 11.3瑕积分的性质与收敛判别 前页 后页 返回
前页 后页 返回 第十一章反常积分 11.1 反常积分概念 11.2 无穷积分的性质与收敛判别 11.3 瑕积分的性质与收敛判别

11.1反常积分概念 一、引例 二、无穷限的广义积分 三、无界函数的广义积分 前 返回
前页 后页 返回 11.1 反常积分概念 一 、 引例 二、无穷限的广义积分 三、无界函数的广义积分 四、小结

一、引例 在讨论定积分时有两个最基本的条件:积分区间 的有穷性;被积函数的有界性 但以下例子告诉我们有时我们需要考虑无穷区间 上的“积分”或无界函数的“积分”. 例1(第二宇宙速度问题)在地球表面垂直发射火 箭,要使火箭克服地球引力无限远离地球,试问初 速度y至少要多大? 前页 后页 返回
前页 后页 返回 一、引例 在讨论定积分时有两个最基本的条件:积分区间 但以下例子告诉我们有时我们需要考虑无穷区间 例1(第二宇宙速度问题)在地球表面垂直发射火 的有穷性; 被积函数的有界性. 上的“积分”或无界函数的“积分”. 箭, 要使火箭克服地球引力无限远离地球, 试问初 速度 v0 至少要多大?

解设地球半径为R,火箭质量为m,地面上的重 力加速度为g,按万有引力定理,在距地心x(2R) 处火箭所受的引力为 F= mgR2 k2 =限KR》 前页 后页 返回
前页 后页 返回 解 设地球半径为 R,火箭质量为 m,地面上的重 处火箭所受的引力为 , 2 2 x mgR F . 1 1 d 2 2 2 R r x mgR x r mgR R 力加速度为 g, 按万有引力定理, 在距地心 x R

当r→+oo时,其极限gR就是火箭无限远离地 球需作的功.于是自然把这一极限写作上限为 +0的积分 厂a=-"ggR 由机械能守恒定律可求初速度'至少应使 号m=mgR 用g=9.81(m/s2),R=6.371×106(m)代入,得 =√2gR≈11.2(km/s): 前页 后页 返回
前页 后页 返回 当 r 时,其极限 mgR 就是火箭无限远离地 的积分 2 2 2 2 d lim d . r R R r mgR mgR x x mgR x x 由机械能守恒定律可求初速度 v0 至少应使 2 0 1 . 2 mv mgR 2 6 用 g R 9.81(m/s ) , 6.371 10 (m) 代入,得 0 v gR 2 11.2 (km/ s). 球需作的功.于是自然把这一极限写作上限为

网2:求曲线v上轴及直线x=,看边所围成的“开巾 曲边梯形”的面积。 y 解:由于这个图形不是封闭的 曲边梯形,而在x轴的正方 y= 向是开口的,即这是的积 分区间为1,∞) 21 0 X 故vb≥1的面积为号=-中=1-方 显然当b改变时,曲边梯形的面积也随之改变, 故b→+时,即m∫=m1-方- 则所求曲边梯形的面积为1 前页
前页 后页 返回 例2: 曲边梯形”的面积。 求曲线 , 轴及直线 1,右边所围成的“开口 1 2 x x x y 0 x y 1 b 2 x 1 y 解:由于这个图形不是封闭的 曲边梯形,而在x轴的正方 向是开口的,即这是的积 分区间为[1,∞), x b dx x b A b b 1 ] 1 1 [ 1 1, 1 2 1 故 则 的面积为 显然当b改变时,曲边梯形的面积也随之改变, ) 1 1 lim (1 1 lim 1 2 b dx x b b b b 故 时,即 则所求曲边梯形的面积为1

二、无穷限的广义积分. 定义1:设函数f(x)在区间[a,+o)上连续,取b>a, 如果极限 m心达存在 则称此极限为函数f(x)在无穷区间[a,+o)上 的广义积分,记作广fx),即 fax)k=im心fx) (1) 前页 后页 返回
前页 后页 返回 二、无穷限的广义积分. 定义1: 设函数 f (x)在区间[a, +)上连续, 取b > a, 如果极限 b b a lim f (x)dx 存在, 则称此极限为函数 f (x)在无穷区间[a, +)上 的广义积分, 记作 ( ) ,即 a f x dx b a b a f (x)dx lim f (x)dx (1)
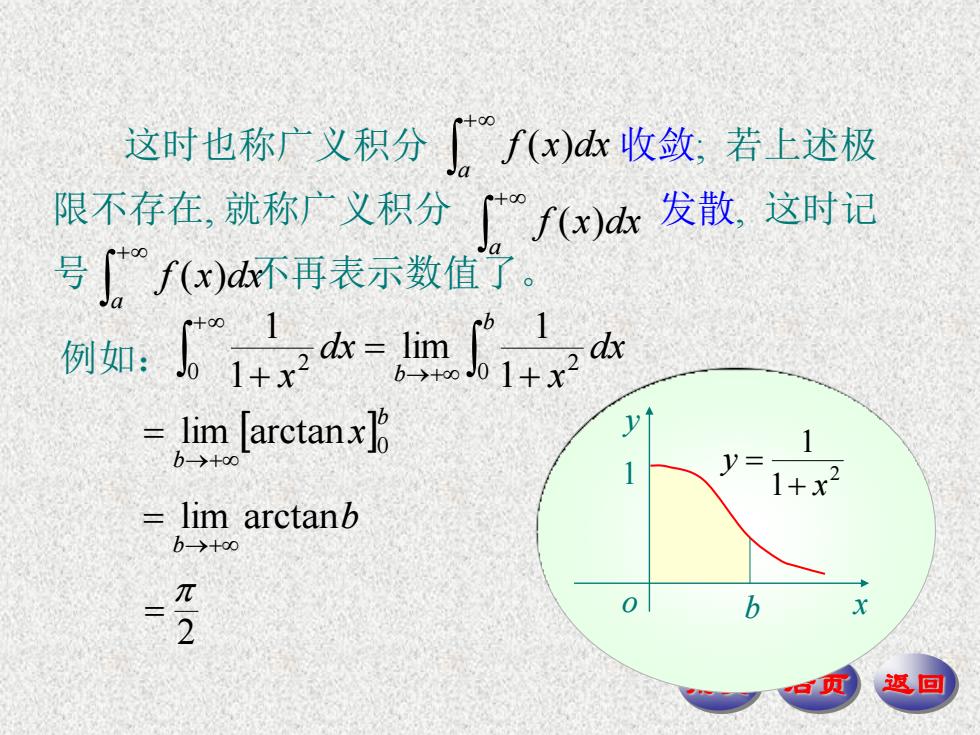
这时也称广义积分f(x)收敛,若上述极 限不存在,就称)广义积分广fx)发散这时记 号∫f(x)d不再表示数值了。 例如:1山-4 lim larctan y 1+x2 lim arctanb b-→+∞ 2 0 返回
前页 后页 返回 这时也称广义积分 收敛; 若上述极 限不存在, 就称广义积分 发散, 这时记 号 不再表示数值了。 a f (x)dx a f (x)dx a f (x)dx 例如: b b dx x dx x 0 2 0 2 1 1 lim 1 1 b b x 0 lim arctan b b lim arctan 2 o y b x 2 1 1 x y 1

类似地,设函数f(x)在区间(一o,b]上连续,取a<b, 如果极限1imf(x)dkr存在,则称此极限为函数 fx)在无穷区间(-∞,b]上广义积分,记作∫心fx) 即 巴f)d=im (2) 这时也称广义积分∫f(x)dc收敛,若上述 极限不存在,就称广义积分f(x)dx发散 前页 后页 返回
前页 后页 返回 类似地, 设函数 f (x)在区间(, b]上连续, 取a < b, 如果极限 b a a lim f (x)dx 存在, 则称此极限为函数 f (x)在无穷区间(, b]上广义积分, 记作 , b a a b f (x)dx lim f (x)dx (2) 这时也称广义积分 收敛; 若上述 极限不存在, 就称广义积分 发散. b f (x)dx b f (x)dx b f (x)dx 即

设函数f(x)在区间(-∞,+∞)上连续,如果广义积分 fx)d和”x)d 都收敛,则称上述两广义积分之和为函数x)在 区间(-o,+o)上广义积分.记作Jf(x),即 rfx)d=心fox)+fax)d limf)ds+limf()ds (3) 这时,也称广义积分f(x)收敛;否则就称 广义积分“f(x)dk发散 上述)义积分统称为无穷限的广义帮爸 后 返回
前页 后页 返回 设函数 f (x)在区间(, +)上连续, 0 0 f (x)dx 和 f (x)dx 都收敛, 则称上述两广义积分之和为函数 f (x)在 区间(, +)上广义积分.记作 ,即 f (x)dx 0 0 f (x)dx f (x)dx f (x)dx b a a b f x dx f x dx 0 0 lim ( ) lim ( ) (3) 这时, 也称广义积分 f (x)dx 收敛; 否则就称 广义积分 发散. f (x)dx 如果广义积分 上述广义积分统称为无穷限的广义积分