
第五节对坐标的曲面积分 一、对坐标的曲面积分的概念与性质 二、对坐标的曲面积分的计算法 三、两类曲面积分的联系
第五节 一、 对坐标的曲面积分的概念与性质 二、对坐标的曲面积分的计算法 三、两类曲面积分的联系 对坐标的曲面积分
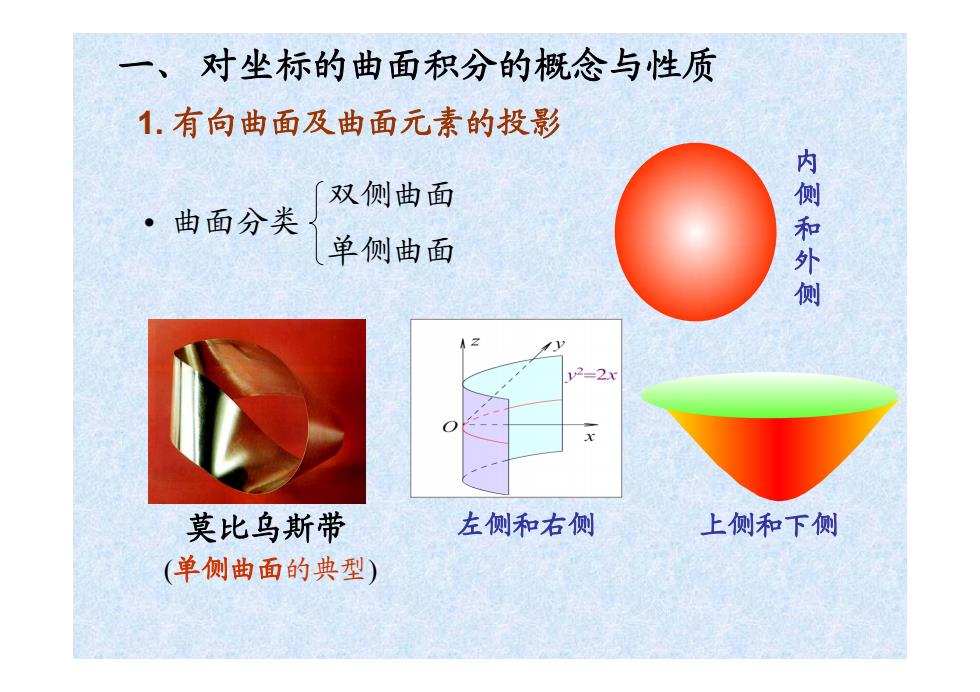
一、 对坐标的曲面积分的概念与性质 1.有向曲面及曲面元素的投影 双侧曲面 ·曲面分类 单侧曲面 内侧和外侧 w2=2x 0 莫比鸟斯带 左侧和右侧 上侧和下侧 (单侧曲面的典型)
1. 有向曲面及曲面元素的投影 • 曲面分类 双侧曲面 单侧曲面 莫比乌斯带 上侧和下侧 内 侧 和 外 侧 左侧和右侧 (单侧曲面的典型) 一 、 对坐标的曲面积分的概念与性质
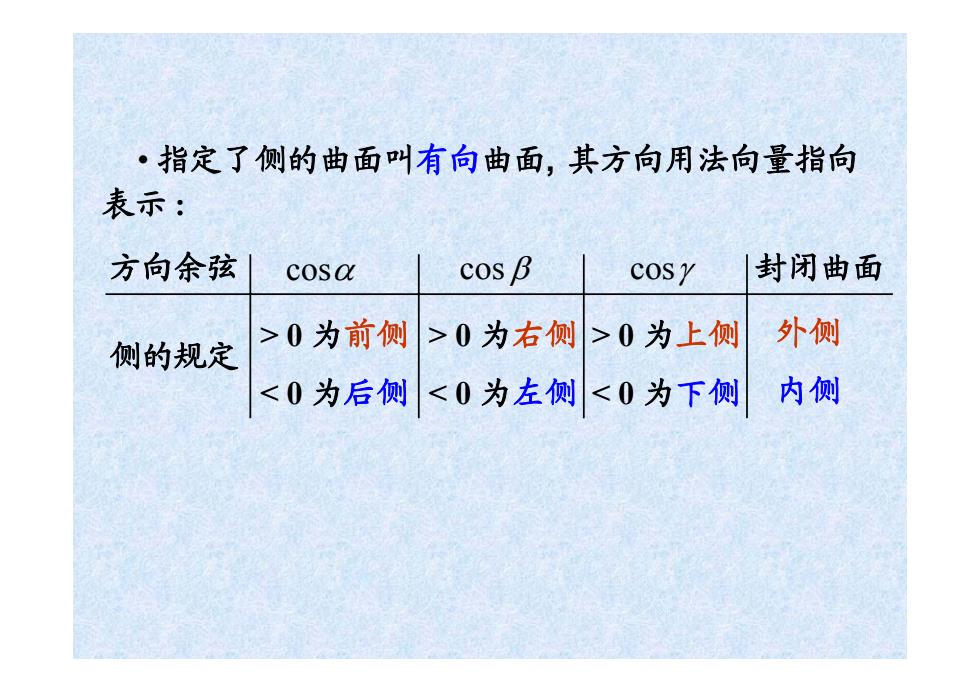
·指定了侧的曲面叫有向曲面,其方向用法向量指向 表示: 方向余弦 cosa cos B cosy|封闭曲面 外侧 侧的规定 >0为前侧>0为右侧>0为上侧 <0为后侧<0为左侧<0为下侧内侧
其方向用法向量指向 方向余弦 cosα cos β cosγ > 0 为前侧 0 为右侧 0 为上侧 < 0 为下侧 外侧 内侧 侧的规定 • 指定了侧的曲面叫有向曲面, 表示 :

设∑为有向曲面,其面元△S在xOy面上的投影记为 (△S)xy,(AS)xy的面积为(△o)xy≥0,则规定 有向投影 (Ao)xy,当cosy>0时 (AS)xy=3-(AG)xy2 当cosy<0时 0, 当cosy=0时 类似可规定(AS)e,(AS)x
设 Σ 为有向曲面, ( ) , xy ΔS ΔS (ΔS) xy = 其面元 在 xOy 面上的投影记为 (Δ ) ≥ 0, S xy σ xy (Δ ) 的面积为 则规定 ( ) , Δσ xy ( ) , − Δσ xy 0 , 当cosγ > 0时 当cosγ < 0时 当cosγ ≡ 0时 有向投影 类似可规定 yz zx (ΔS) , (ΔS)

2.对坐标的曲面积分的概念 定义设∑为光滑的有向曲面,函数y,z在∑上有 界,把∑分成块小曲面△S,(△S,同时又表示第块小曲面 的面积),AS在x0y面上的投影为(AS)o,(5,n,5)是 △S;上任意取定的一点,如果当各小块曲面的直径的最大 值2→0时, im2R5,n-5aS),记作∬R(x,z)dd 2-→0 j=1 存在,则称此极限为函数R(x,y,z)在有向曲面∑上对坐 标x,y的曲面积分(也称第二类曲面积分) R(X,y,z):被积函数 ∑:积分曲面
2.对坐标的曲面积分的概念 定义 设Σ为光滑的有向曲面,函数 x y 在Σ上有 界,把Σ分成n块小曲面ΔSi(ΔSi同时又表示第 i块小曲面 的面积 ),ΔSi在xoy面上的投影为 Si xy (Δ ) , ( , , ) i i i ξ η ζ 是 ΔSi上任意取定的一点,如果当各小块曲面的直径的最大 λ →0 时, R( , ,z) 值 ∑ = → Δ n i R i i i Si xy 1 0 lim (ξ ,η ,ζ )( ) λ 存在, 则称此极限为函数R(x, y,z)在有向曲面Σ上对坐 标x, y的曲面积分(也称第二类曲面积分) ∫∫ Σ R(x, y,z)dxdy 记作 R(x, y,z):被积函数 Σ:积分曲面

类似可定义 ∬P(x,yz)k=lm∑P(5,n,5,AS,) 2→0 i1 称为P(化,3,)在有向曲面∑上对”,z的曲面积分; ∬x,zt=m∑(5,n,5△s)x 2-→0 i=1 称为Q(化,y,)在有向曲面∑上对乙,x的曲面积分;
类似可定义 ∫∫ ∑ = → Σ = Δ n i P i i i Si yz P x y z dydz 1 0 ( , , ) lim (ξ ,η ,ζ )( ) λ ∫∫ ∑ = → Σ = Δ n i dzdx Q i i i Si zx Q x y z 1 0 ( , , ) lim (ξ ,η ,ζ )( ) λ 称为P (x, y, z)在有向曲面∑上对 y, z 的曲面积分; 称为Q (x, y, z)在有向曲面∑上对 z , x 的曲面积分;
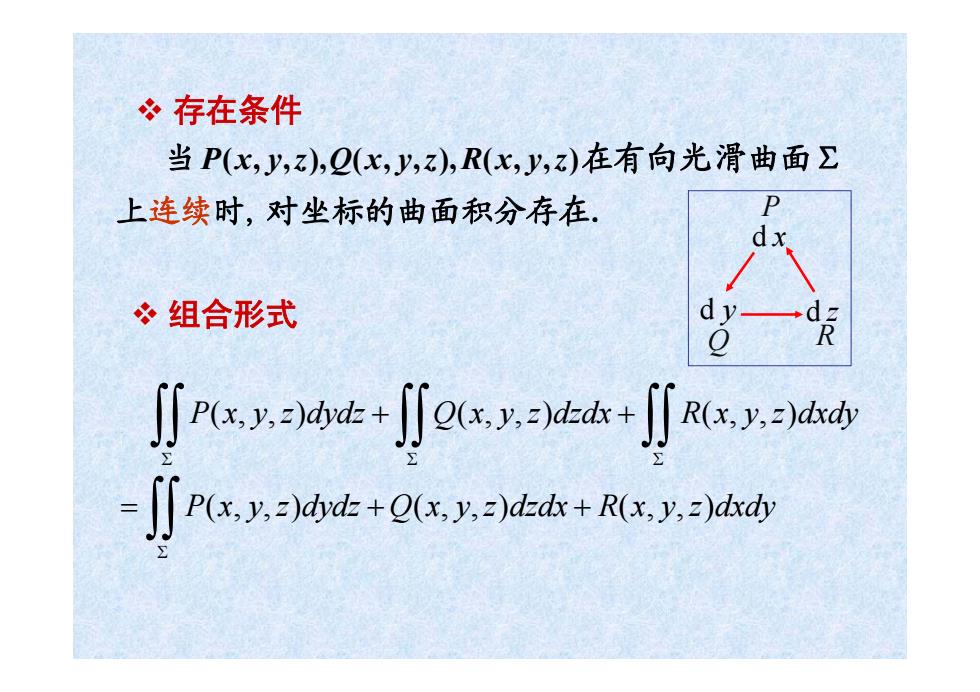
冬存在条件 当P(x,Jy,z),2(x,y,z),R(x,y,z)在有向光滑曲面∑ 上连续时,对坐标的曲面积分存在 冬组合形式 ∬ [JP(*.y.-)dvd-+Q(x.y.)d-ds+R(x.y.-)dsdy
d x d y d z P Q R P x y z dydz Q x y z dzdx R x y z dxdy (, ,) (, ,) (, ,) Σ = ++ ∫∫ 存在条件 当 P ( x , y , z), Q ( x , y , z), R ( x , y , z )在有向光滑曲面Σ 上连续 时, 对坐标的曲面积分存在. 组合形式 P x y z dydz Q x y z dzdx R x y z dxdy (, ,) (, ,) (, ,) ΣΣΣ + + ∫∫ ∫∫ ∫∫
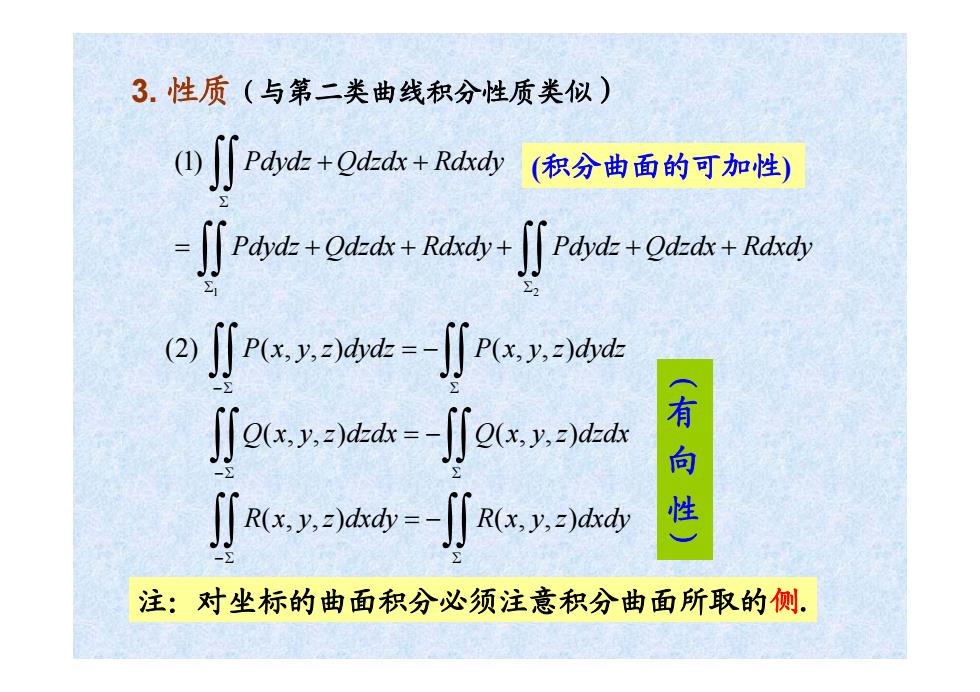
3.性质(与第二类曲线积分性质类似) (JJPdy-+Qd-ds+Rdsdy (积分曲面的可加性) ∬Pat+Qth:h+jPat+0k+nh 2jPxt-∬Pwt ∬oxyh-∬O.y.l-d 有 ∬R(xyhd-J∫F3.).zydso 注:对坐标的曲面积分必须注意积分曲面所取的侧
3. 性质(与第二类曲线积分性质类似) 1 2 (1) Pdydz Qdzdx Rdxdy Pdydz Qdzdx Rdxdy Pdydz Qdzdx Rdxdy Σ Σ Σ + + = +++ ++ ∫∫ ∫∫ ∫∫ (2) ( , , ) ( , , ) (, ,) (, ,) (, ,) (, ,) P x y z dydz P x y z dydz Q x y z dzdx Q x y z dzdx R x y z dxdy R x y z dxdy −Σ Σ −Σ Σ −Σ Σ = − = − = − ∫∫ ∫∫ ∫∫ ∫∫ ∫∫ ∫∫ 注:对坐标的曲面积分必须注意积分曲面所取的侧. (积分曲面的可加性) (有 向 性)

二、对坐标的曲面积分的计算法 设光滑曲面∑:z=z(x,y),(x,y)∈Dxy取上侧, R(x,y,z)是上的连续函数,则 J∬x=ddy-∬风xg(,1dxdy 注:若曲面∑取下侧,则 J∬Rz.y.-)dxdy=-j∬Rxy(x1dxdy 一投,二代,三定号(上侧为正,下侧为负)
二、对坐标的曲面积分的计算法 设光滑曲面 D x y Σ : z = z ( x, y ), ( x, y ) ∈ 取上侧 , R ( x, y,z ) 是 Σ 上的连续函数, 则 R( , , )d d xyz x y Σ ∫∫ [ , , ] D x y = Rxy ∫∫ z ( x, y ) d x d y 注:若曲面Σ取下侧,则 R( , , )d d xyz x y Σ ∫∫ [ , , ] D x y = Rxy ∫∫ — z ( x, y ) d x d y 一投,二代,三定号(上侧为 正,下侧为 负 )

若∑:x=x(y,),(y,)∈Dz,则有(前正后负) =t∬P0,,yd 若∑:y=y(z,x),(z,x)eDx,则有(右正左负) jxyd:dx=±∬ox(e),-ldzdx D 一投,二代,三定号
• 若 : ( , ), ( , ) , Dyz Σ x = x y z y z ∈ 则有 P( , , )d d xyz yz Σ ∫∫ [ , ] Dy z = ± P y, z ∫∫ x( y,z) d y d z • 若 : ( , ), ( , ) , Dzx Σ y = y z x z x ∈ 则有 Qxyz z x ( , , )d d Σ ∫∫ [ , , ] Dz x = ± Qx z ∫∫ y(z, x) d z d x (前正后负) (右正左负) 一投,二代,三定号