
第二节对坐标的曲线积分 一、对坐标的曲线积分的概念 与性质 二、对坐标的曲线积分的计算法 三、两类曲线积分之间的联系
第二节 一、对坐标的曲线积分的概念 与性质 二、 对坐标的曲线积分的计算法 三、两类曲线积分之间的联系 对坐标的曲线积分
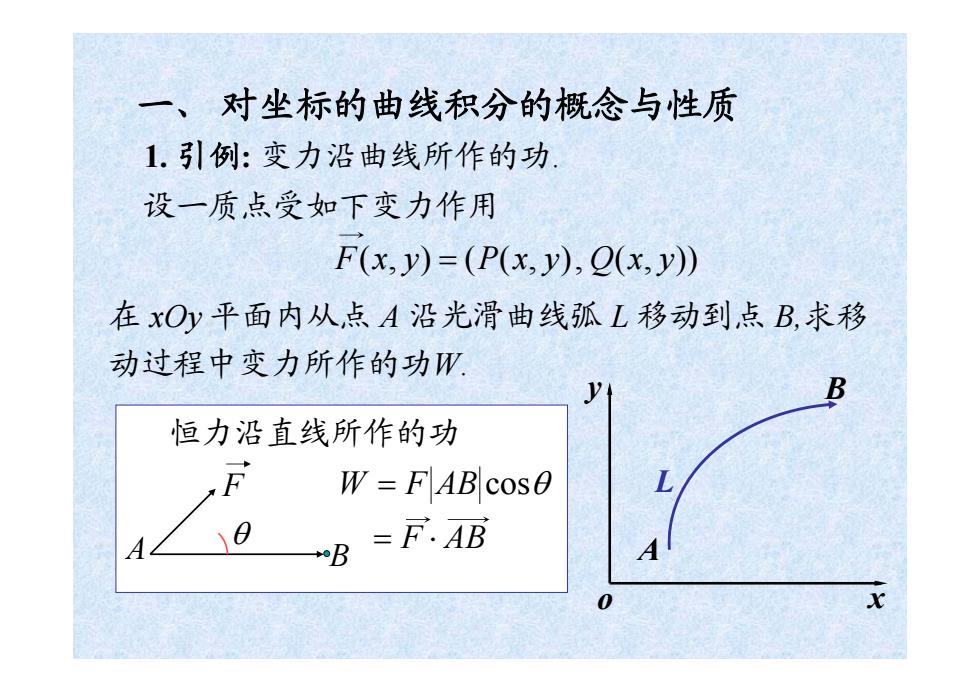
一、对坐标的曲线积分的概念与性质 1.引例:变力沿曲线所作的功. 设一质点受如下变力作用 F(x,y)=(P(x,y),Q(x,y)) 在xOy平面内从点A沿光滑曲线孤L移动到点B,求移 动过程中变力所作的功W y 恒力沿直线所作的功 F W=FAB cos0 A B =F.AB
一 、 对坐标的曲线积分的概念与性质 1. 引例: 变力沿曲线所作的功. 设一质点受如下变力作用 在 xOy 平面内从点 A 沿光滑曲线弧 L 移动到点 B, 求移 W = F AB cosθ 恒力沿直线所作的功 动过程中变力所作的功W. = F ⋅ AB A B F θ F(x, y) = (P(x, y), Q(x, y)) o x y A B L
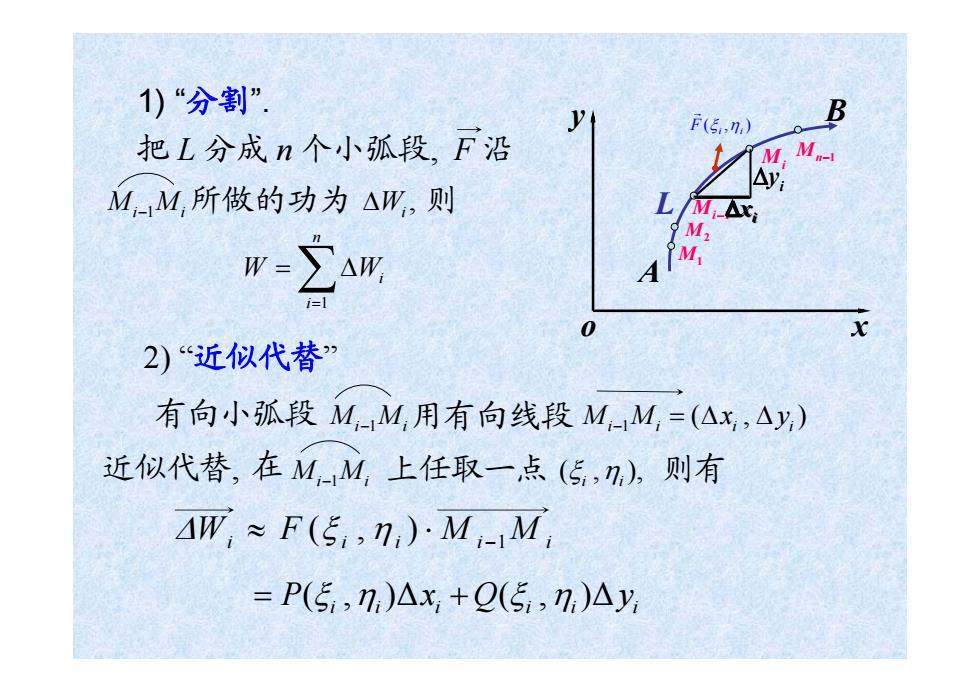
1)“分割” F(5,n) 把L分成n个小孤段,F沿 MM,所做的功为△W,则 L/MAx M, i=1 2)“近似代替” 有向小孤段M,-M,用有向线段M,-M,=(△x,△y) 近似代替,在MM,上任取一点(5,n),则有 AW,≈F(51,7,)M-M =P(5,7,)△x,+Q(5,7)△y
1) “分割”. 2) “近似代替” = + P(, ) ξii i ii i η ξη ΔxQ y (, )Δ F 沿 1 (, ) ΔW F MM i ii i i ≈ ⋅ ξ η − 把 L 分成 n 个小弧段, 所做的功为 , ΔWi 1 n i i W W = = Δ ∑ Mi i −1M 则 o x y A B L Mn−1 Mi Mi−1 M2 M1 Δxi i Δy (, ) F i i ξ η G 有向小弧段 (, ) i i = Δ Δ x y 近似代替, ( , ), i i ξ η 则有 用有向线段 在 上任取一点 Mi i −1M Mi i −1M Mi i −1M i Δx

3)“求和” W≈ ∑[P(5,n)△x+Q5,n)△y 4)“取极限” W lim 2)0 ∑[P(5,7,)△x+05,7)△y] i=l (其中入为n个小孤段的 F(5,n) 最大长度) /Mi-Ax A
3) “求和” 4) “取极限” 1 n i W = ≈∑ 0 1 lim n i W λ→ = = ∑ (其中λ 为 n 个小弧段的 最大长度) o x y A B L Mn−1 Mi Mi−1 M2 M1 i Δx i Δy (, ) F i i ξ η G [P(, ) ξη ξη ii i ii i ΔxQ y + (, )Δ ] [P(, ) ξη ξη ii i ii i ΔxQ y + (, )Δ ]

2.定义.设L为xOy平面内从A到B的一条有向光滑 孤,函数P(x,y)、Qx,y)在L上有界.若对L的任意分割 和在局部孤段上任意取点,极限 Im2P(E,WA作Ax达 λ→0 总存在,称此极限为函数P(x,y)在有向曲线孤L上对 坐标x的曲线积分. 类似地,如果板限m主05M0xd 101 总存在,称此极限为函数Qx,y)在有向曲线弧L上对 坐标y的曲线积分
2. 定义. 设 L 为xOy 平面内从 A 到B 的一条有向光滑 弧, 和在局部弧段上任意取点, 极限 函数P(x, y)、Q(x, y)在L上有界. 若对L的任意分割 总存在, 称此极限为函数P(x, y)在有向曲线弧L上对 坐标x 的曲线积分. i i i n i P Δx → = lim∑ ( , ) 1 0 ξ η λ ∫LP(x, y)dx =记作 类似地,如果极限 在有向曲线弧L上对 i i i n i Q Δy → = lim∑ ( , ) 1 0 ξ η λ ∫LQ(x, y)dy 总存在, 称此极限为函数Q(x, y) = 记作 坐标y的曲线积分. 类似地,如果极限 i i i n i Q Δy → = lim∑ ( , ) 1 0 ξ η λ

说明 1.在积分中P(x,y)、Q(x,y)叫做被积函数,L叫做积分孤段 2对坐标的曲线积分也称为第二类曲线积分 推广 设「为空间内一条光滑有向曲线孤,函数P(x,y,z)小 Q(x,y,)、R(x,y,z)在「上有定义.我们定义 P(x.y.)ds=lim>P(G)Ax. →0≥1 ∫0xy,a=lim205n,54y, →0i-1 ∫Rxy,adt=limR5,n,5A →0-1
1.在积分中P(x, y)、Q(x, y)叫做被积函数, L叫做积分弧段. 说明 2.对坐标的曲线积分也称为第二类曲线积分. i i i i n i LQ x y z dy = Q Δy → = ∫ ( , , ) lim∑ ( , , ) 1 0 ξ η ζ λ , 设Γ为空间内一条光滑有向曲线弧, 函数P(x, y, z)、 Q(x, y, z)、R(x, y, z)在Γ上有定义. 我们定义 i i i i n i L P x y z dx = P Δx → = ∫ ( , , ) lim∑ ( , , ) 1 0 ξ η ζ λ , 推广 i i i i n i L R x y z dz = R Δz → = ∫ ( , , ) lim∑ ( , , ) 1 0 ξ η ζ λ

对坐标的曲线积分的简写形式 在应用上经常出现的是 P(dy, 上式可记为 ∫Px,k+Oxd,或JFx,)dr, 其中Fx,y)=P(x,y)i4Q(x,yj,dr=dxi+dji 对三元函数来说,就有 Pds+Qdy+Rd==Pdsx+Qdy+Rd==S A-dr, A=P(x,y,z)i+e(x,y,)j+R(x,y,z)k,dr=dxi+dyj+dzk
对坐标的曲线积分的简写形式 在应用上经常出现的是 ∫ ∫ + L L P ( x, y )dx Q ( x, y )dy , 上式可记为 其中 F(x , y ) =P (x, y ) i+ Q (x, y)j, dr =dx i+dyj. 对三元函数来说 ,就有 其中 A =P(x, y, z)i +Q(x , y , z)j+R (x, y, z ) k , dr=dx i+dyj+dzk. Pdx Qdy Rdz ∫ ∫ ∫ Γ Γ Γ + + = Pdx +Qdy +Rdz ∫Γ A dr L = ⋅ ∫ , P x y dx Q x y dy L ( , ) + ( , ) ∫ , 或 ∫L F ( x, y ) d . r

3.对坐标的曲线积分的性质 性质1设a、B为常数,则 Jl@F(x)+BF(x.dr=aJFi(x.y)dr+BJF(x.)dr 性质2若有向曲线孤L可分成两段光滑的有向曲线孤L和 L2,则 Fdr-FdFdr 性质3设L是有向光滑曲线孤,L是L的反向曲线孤,则 JF(x.y)-dr=-JF(dr. 注:对坐标的曲线积分必须注意积分孤段的方向!
3.对坐标的曲线积分的性质 •性质1 设 α、 β为常数, 则 ∫ ∫ ∫ + ⋅ = ⋅ + ⋅ L L L [ F ( x, y ) F ( x, y)] dr F ( x, y ) dr F ( x, y ) dr α 1 β 2 α 1 β 2 •性质2 若有向曲线弧 L可分成两段光滑的有向曲线弧 L1和 L2, •性质3 设 L是有向光滑曲线弧, L− 是 L的反向曲线弧, 则 ∫ ∫ ⋅ = − ⋅ −L L F ( x, y ) dr F ( x, y ) dr . ∫ ∫ ∫ ⋅ = ⋅ + ⋅ 1 2 ( , ) ( , ) ( , ) L L L 则 F x y dr F x y dr F x y dr . 注: 对坐标的曲线积分必须注意积分弧段的方向 !

二、对坐标的曲线积分的计算法 定理:设P(x,y),Q(x,y)在有向光滑孤L上有定义且 连续,L的参数方程为 二00,L的起点和终点对应 y=w(t) 的参数分别为a和B,则曲线积分∫P(+Qxy存在 且有 JP(x.ydx+Q(x.y)dy -(Plw1+Ql.vilw)dr 注意:①下限对应于L的起点,上限B对应于L的终点, ②a不一定小于B
二、对坐标的曲线积分的计算法 定理 : 设 P ( x, y ), Q ( x, y ) 在有向光滑弧 L 上有定义且 L 的参数方程为 ⎩ ⎨ ⎧ = = ( ) ( ) y t x t ψ ϕ ∫ + L P ( x, y ) d x Q ( x, y ) d y { ∫ = β α P [ϕ ( t), ψ ( t)] ϕ′( t ) + Q [ϕ ( t), ψ ( t)] ψ′( t ) } d t 连续, , L的起点和终点对应 的参数分别为 α和 β, 则曲线积分 存在, ∫ + L P(x, y)dx Q(x, y)dy 且有 注意: ①下限 α对应于 L的起点 , 上限β 对应于 L的终点 , ② α不一定小于 β

特殊情形 (I)L:y=y(x)起点横坐标x=a,终点x=b. 则JP+Q=∫PLx,r(x+OIx,(xy'(x. a对应L的起,点 b对应L的终点 (2)L:x=x(y)起点纵坐标y=c,终点y=d. 则∫P+d=J{PIx)JyxO)+0Ix()
特殊情形 (1) L : y = y(x) 起点横坐标 x = a,终点 x = b. Pdx Qdy {P[x, y(x)] Q[x, y(x)]y (x)}dx. b ∫L ∫a + = + ′ (2) L : x = x( y) 起点纵坐标 y = c,终点 y = d. Pdx Qdy {P[x( y), y]x ( y) Q[x( y), y]}dy. d ∫L ∫c + = ′ + 则 则 a对应L的起点 b对应L的终点