
第十一章 曲线积分与曲面积分 积分学 定积分二重积分三重积分曲线积分曲面积分 积分域 区间 平面域 空间域 曲线孤 曲面域 对孤长的曲线积分 曲线积分 对坐标的曲线积分 对面积的曲面积分 曲面积分 对坐标的曲面积分
第十一章 积分学 定积分二重积分三重积分 积分域 区 间 平面域 空间域 曲线积分 曲线弧 曲面域 曲线积分 曲面积分 对弧长的曲线积分 对坐标的曲线积分 对面积的曲面积分 对坐标的曲面积分 曲面积分 曲线积分与曲面积分

第一节对孤长的曲线积分 一、对孤长的曲线积分的概念与性质 二、对孤长的曲线积分的计算法
第一节 一、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法 对弧长的曲线积分
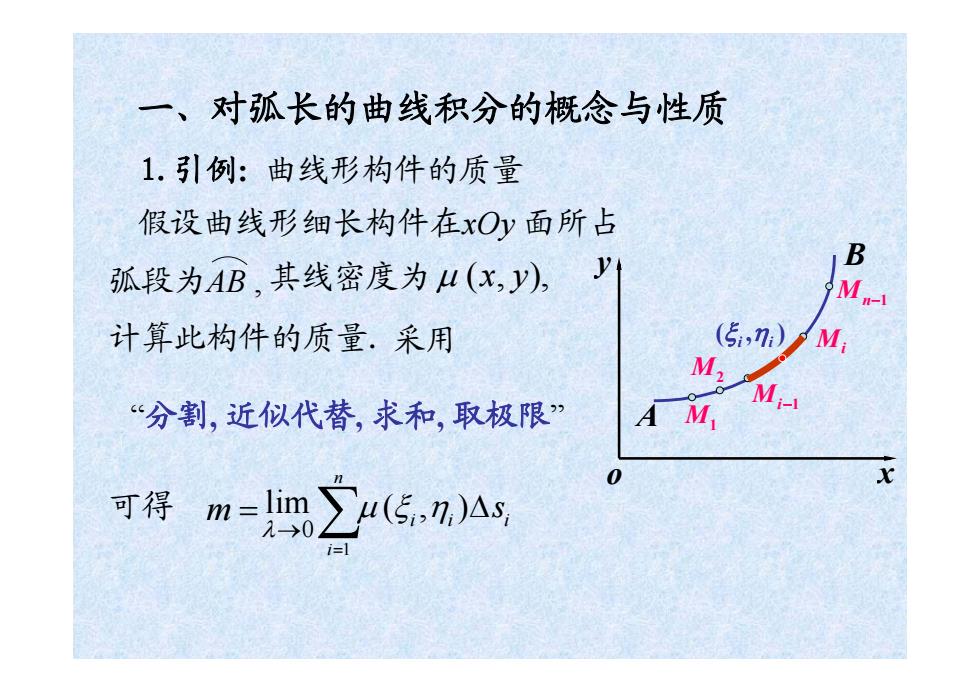
一、对孤长的曲线积分的概念与性质 1.引例:曲线形构件的质量 假设曲线形细长构件在xOy面所占 y B 孤段为AB,其线密度为u(x,y) M 计算此构件的质量.采用 (5,n)M M22 “分割,近似代替,求和,取极限” A M 可得m=∑4(5nA
一、对弧长的曲线积分的概念与性质 假设曲线形细长构件在xOy 面所占 弧段为AB , 其线密度为 μ ( , ), x y “分割, 近似代替, 求和, 取极限” (, ) ii i 可得 μ ξ η Δ s 1 n i= m = λ lim → 0 ∑ 计算此构件的质量. 1.引例 : 曲线形构件的质量 采用 o x y A B Mn − 1 Mi Mi− 1 M2 M1 ( , ) ξ i ηi

2.定义 设L是xOy面中一条光滑的曲线孤,函数f(x,y)是定 义在L上的一个有界函数,若通过对L的任意分割和对 局部的任意取点,下列“乘积的和式极限” 立w 积分孤段 被积函数 都存在,则称此极限为函数f(x,y)在曲线孤L上对孤长 的曲线积分,或第一类曲线积分
设 L是xOy 面中一条光滑的曲线弧,函数 是定 义在 L上的一个有界函数, 都存在, f (, ) x y 的曲线积分, = 记作 ( , )d L f xy s ∫ 若通过对 L的任意分割 局部的任意取点, 2.定义 f (, ) x y 下列“乘积的和式极限” 则称此极限为函数 在曲线弧L上对弧长 或第一类曲线积分. 积分弧段 被积函数 0 lim λ→ 和对 (, ) ii i f ξ η Δs 1 n i= ∑

曲线形细长构件的质量 m=2(5,nA=∫4(xnds i= 注:1.若函数f(x,y)在光滑的曲线孤L上连续,则 ∫fcd娱存在的 2.如果L是闭曲线,则记为f,fx,)ds 推广:/xyds=m2/5m,5 其中厂是空间曲线孤
( , )d L = μ xy s ∫ 曲线形细长构件的质量 (, ) ii i μ ξ η Δs 1 n i= m =λlim→0∑ 注:1.若函数 f (, ) x y 在光滑的曲线弧L上连续,则 ( , )d L f xy s ∫ 是存在的. 推广: f (, ,) x y z ds ∫Γ i ( , , )Δs i i i ∑ f ξ η ζ =ni 1 0 lim→ = λ 其中 Γ 是空间曲线弧. 2.如果 L 是闭曲线 , 则记为 ( , )d . ∫L f x y s

3.性质 a,B为常数 0u+gx明s-aJro.d+j8xa Qjads-xds+Jx0 (L分成L,L2两段) (3)设在L上f(x,y)≤g(x,y),则 ∫f.y)ds≤∫8x0ds 特别 sa∫la (4∫ds=1(1为曲线孤L的长度)
3. 性质 (1) ( , ) ( , ) d [ ] L α β f xy gxy s + ∫ ( L 分成 两段) 1 2 L L, ( l 为曲线弧 L 的长度) ( , )d ( , )d L L = + α β f xy s gxy s ∫ ∫ = l 1 2 (2) ( , )d ( , )d ( , )d LL L f xy s f xy s f xy s = + ∫ ∫ ∫ (4) d L s ∫ ( , )d ( , )d L L f xy s gxy s ≤ ∫ ∫ (3) 设在L上 则 f ( , ) ( , ), xy gxy ≤ α, β 为常数 特别 ( , )d ( , ) d L L f x y s ≤ f x y s ∫ ∫

3.性质 凸,B为常数 0jIc+gjs=ajxds+j8xd 2∫/d-xd+fas (L分成L,L2两段) (3)设在L上f(x,y)≤g(xy),则 ds≤∫300a 特别 xwdjnas (④∫ds=1(1为曲线弧L的长度)
3. 性质 (1) ( , ) ( , ) d [ ] L α β f xy gxy s + ∫ ( L 分成 两段) 1 2 L L, ( l 为曲线弧 L 的长度) ( , )d ( , )d L L = + α β f xy s gxy s ∫ ∫ = l 1 2 (2) ( , )d ( , )d ( , )d LL L f xy s f xy s f xy s = + ∫ ∫ ∫ (4) d L s ∫ ( , )d ( , )d L L f xy s gxy s ≤ ∫ ∫ (3) 设在L上 则 f ( , ) ( , ), xy gxy ≤ α, β 为常数 特别 ( , )d ( , ) d L L f x y s ≤ f x y s ∫ ∫

二、对孤长的曲线积分的计算法 基本思路:求曲线积分 转化计算定积分 定理:设f(x,y)是定义在光滑曲线孤 L:x=p(t),y=w(t)(a≤t≤B) 上的连续函数则曲线积分∫,fx,)ds存在,且 Jf.ds-tw+d
二、对弧长的曲线积分的计算法 基本思路 : 转 化 计算定积分 定理 : 设 f ( x, y ) 且 y = ψ ( t ) (α ≤ t ≤ β ) 上的连续函数, 是定义在光滑曲线弧 则曲线积分 L : x = ϕ ( t ), ( , ) d 存在, ∫L f x y s 求曲线积分 ∫ ∫ = ′ + ′ β α f x y s f ϕ t ψ t ϕ t ψ t t L ( , ) d [ ( ), ( )] ( ) ( ) d 2 2

x=φ(t) 曲线孤的方程L: (a≤t≤B) y=(t) 令x=(t) y=w() ds=()+w(t)dt Jf.yds-.d 说明:积分限必须满足<阝 下限必须小于 上限
说明: 积分限必须满足α < β ! x = φ ( )t y t =ψ ( ) 2 2 d ( ) ( )d s t tt = + φ ψ ′ ′ ( ) : () ( ) x t L t y t φ α β ψ ⎧ = ⎪⎨ ≤ ≤ ⎪⎩ = 曲线弧的方程 令 下限必须小于 上限 ∫ ∫ = ′ + ′ βα f x y s f ϕ t ψ t ϕ t ψ t t L ( , )d [ ( ), ( )] ( ) ( ) d 2 2

如果曲线L的方程为y=W(x)(a≤x≤b),则有 f.d(dx 令y=(x) ds=I+(y)dx 如果方程为极坐标形式:L:r=r(0)(@≤0≤B),则 f(xy)ds -f(r(cs0)sin)d x=rcose y=rsin ds=vr2+(r)"de
如果曲线 L 的方程为y =ψ(x) (a ≤ x ≤ b),则有 ∫L f (x, y)ds 如果方程为极坐标形式: L :r = r(θ ) (α ≤θ ≤ β ),则 f x y s L∫ ( , )d ∫ = βα f (r(θ ) cosθ , r(θ )sinθ ) 1 (x) dx 2 +ψ′ (θ ) (θ ) dθ 2 2 r + r′ ∫ = ba f (x,ψ (x)) y =ψ ( ) x 2 令 d 1 ( )d s = + y′ x x r = cosθ y r = sinθ 2 2 d ()d srr = + ′ θ