
第七节斯托克斯公式 一、斯托克斯公式
第七节 斯托克斯公式 一、斯托克斯公式

斯托克斯(1819-1903) 英国数学物理学家.他是19世纪英国 数学物理学派的重要代表人物之一,其 主要兴趣在于寻求解重要数学物理问题 的有效且一般的新方法,在1845年他导 出了著名的粘性流体运动方程(后称之 为纳维-斯托克斯方程),1847年先于 柯西提出了一致收敛的概念.他提出的斯托克斯公式 是向量分析的基本公式.他一生的工作先后分五卷 出版
斯托克斯(1819-1903) 英国数学物理学家. 他是19世纪英国 数学物理学派的重要代表人物之一, 其 主要兴趣在于寻求解重要数学物理问题 的有效且一般的新方法, 在1845年他导 出了著名的粘性流体运动方程 ( 后称之 为纳维 – 斯托克斯方程 ), 1847年先于 柯西提出了一致收敛的概念. 他提出的斯托克斯公式 是向量分析的基本公式. 他一生的工作先后分 五卷 出版

一、 斯托克斯公式 定理1设光滑曲面∑的边界「是分段光滑曲线,∑的 侧与「的正向符合右手法则,P,Q,R在包含Σ在内的一 个空间域内具有连续一阶偏导数,则有 )vd--o) =dx+ 80 dxdy -fPdx+Qdy+Rdz (斯托克斯公式) 斯托克斯公式的实质: 表达了有向曲面上的曲面积分与其边界曲线上的曲 线积分之间的关系
一、 斯托克斯公式 定理1 设光滑曲面Σ 的边界Γ 是分段光滑曲线, x y y P x Q z x x R z P y z z Q y R d d d d ⎟d d ⎠⎞ ⎜⎝⎛ ∂∂ − ∂∂ ⎟ + ⎠⎞ ⎜⎝⎛ ∂∂ − ∂∂ ⎟ + ⎠⎞ ⎜⎝⎛ ∂∂ − ∂∂ ∫∫Σ ∫ = + + ΓPd x Qd y Rd z (斯托克斯公式) 个空间域内具有连续一阶偏导数, Σ 的 侧与 Γ 的正向符合右手法则, P,Q,R在包含Σ 在内的一 则有 斯托克斯公式的实质: 表达了有向曲面上的曲面积分与其边界曲线上的曲 线积分之间的关系

证:情形1.∑与平行z轴的直线只交于 一点,设其方程为 :z=f(x,y),(x,y)∈Dxy 为确定起见,不妨设∑取上侧 则fPdx=fePx,yc.)dx -ody刘 -n,g得d 号2ksa的
y z x Σ O Γ 证: 情形1. Σ 与平行 z 轴的直线只交于 一点, 设其方程为 Dx y Σ : z = f (x, y), (x, y)∈ n 为确定起见, 不妨设Σ 取上侧. Dx yC 则 ∫Γ Pd x ∫ = C P(x, y,z(x, y))d x P x y z x y x y Dx y y ( , , ( , ))d d ∫∫ ∂∂ = − [ ] x y y z z P y P Dx y d d ∂∂ ∂∂ + ∂∂ = −∫∫ [ f ] S z P y P y cosγ d Σ ∂∂ + ∂∂ = −∫∫ (利用格林公式)

oy=s=m会 cos B cos y 因此 毛a-儿g lcosyds X Pcosy lds -j8 aPaxdy Oy
2 2 1 1 cos , x y f f γ + + = cos , 2 2 1 x y y f f f + + − β = cos cos y f β γ = − y z x Σ O Γ n D x y C 因此 [ ] S z P y P P x cos d cos cos d γ γ β Γ Σ ∂ ∂ − ∂ ∂ = − ∫ ∫∫ [ ] S y P z P cos β cos γ d Σ ∂ ∂ − ∂ ∂ = ∫∫ x y y P z x z P d d d d ∂ ∂ − ∂ ∂ = ∫∫Σ

f,ar-小8ddx-号 dxdy 同理可证 f,0ay-川94dy号 yd 人nax-1a:- d=dx x 三式相加,即得斯托克斯公式;
同理可证 ∫Γ Qd y y z zQ x y xQ d d d d ∂∂ − ∂∂ = ∫∫Σ ∫Γ Rd x z x xR y z yR d d d d ∂∂ − ∂∂ = ∫∫Σ 三式相加, 即得斯托克斯公式 ; ∫Γ Pd x x y yP z x zP d d d d ∂∂ − ∂∂ = ∫∫Σ

情形2曲面∑与平行z轴的直线交点多于一个,则可 通过作辅助线把∑分成与z轴只交于一点的几部分, 在每一部分上应用斯托克斯公式,然后相加,由于沿辅助 曲线方向相反的两个曲线积分相加刚好抵消,所以对这 类曲面斯托克斯公式仍成立. 注意:如果∑是xOy面上的一块平面区域,则斯托克斯 公式就是格林公式,故格林公式是斯托克斯公式的特例. 格林公式 卷广 斯托克斯公式
情形2 曲面Σ 与平行 z 轴的直线交点多于一个, 则可 通过作辅助线把 Σ 分成与z 轴只交于一点的几部分, 在每一部分上应用斯托克斯公式, 然后相加, 由于沿辅助 曲线方向相反的两个曲线积分相加刚好抵消, 所以对这 类曲面斯托克斯公式仍成立. 注意: 如果Σ 是 xOy 面上的一块平面区域, 则斯托克斯 公式就是格林公式, 故格林公式是斯托克斯公式的特例. 格林 公式 斯托克斯公式 推广

为便于记忆,斯托克斯公式还可写作: dydz dzdx dxdy o 8x Oy 0z -fPdx+Qdy+Rd: P Q R 或用第一类曲面积分表示: cosa cos B cosy S A a-小Q aaR dS=fPdx+Ody+Rd=
为便于记忆, 斯托克斯公式还可写作: ∫∫ ∂∂ ∂∂ ∂∂ Σ P Q R x y z d y d z d z d x d x d y ∫ = + + ΓPd x Qd y Rd z 或用第一类曲面积分表示: S P Q R x y z d cos cos cos ∫∫ ∂∂ ∂∂ ∂∂ Σ α β γ ∫ = + + ΓPd x Qd y Rd z

例1.利用斯托克斯公式计算积分,dx+xdy+ydz 其中厂为平面x+y+z=1被三坐标面所截三角形的整 个边界,方向如图所示 解:记三角形域为∑,取上侧,则 fzdx+xdy+yd= dydz dzdx dxdy = 品 品 品 x y -eau:+d:dx4dd-ouxdy-月 利用对称性
z x y 1 1 1 O z x y y z z x x y x y ∂ z ∂ ∂ ∂ ∂ ∂ ∫∫ = d d d d d d Σ 例1. 利用斯托克斯公式计算积分∫ + + Γ z d x x d y y d z 其中Γ 为平面 x+ y+ z = 1 被三坐标面所截三角形的整 解: 记三角形域为Σ , 取上侧,则 个边界, 方向如图所示. ∫ + + Γ z d x x d y y d z ∫∫ = + + Σd y d z d z d x d x d y 利用对称性 ∫∫ = Dx y 3 d x d y 23 = Dxy
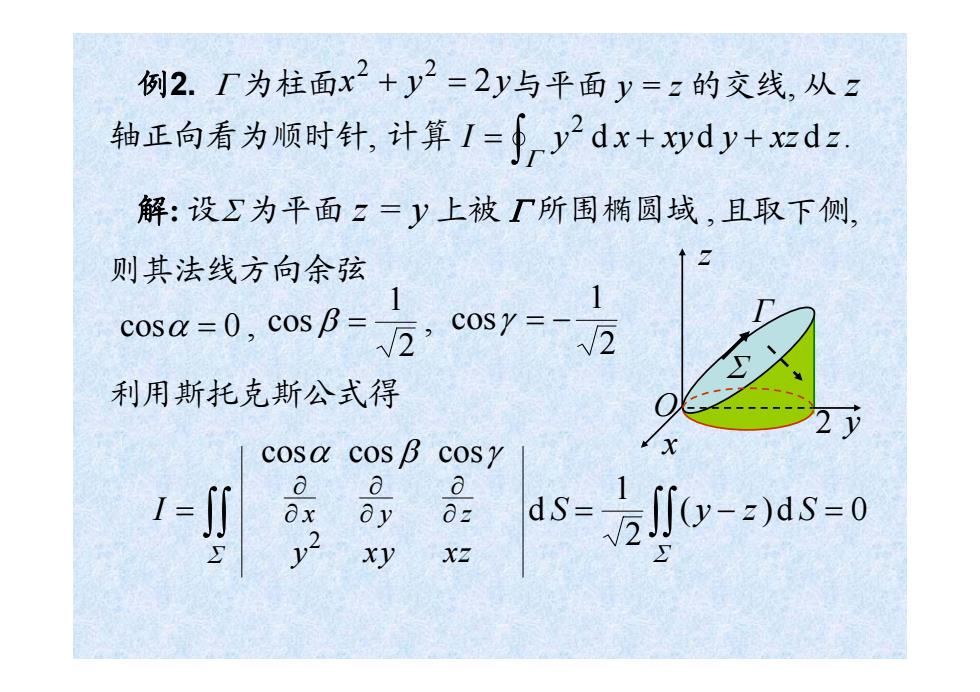
例2.Γ为柱面x2+y2-2y与平面y=z的交线,从2 轴正向看为顺时针,计算/=∫rydx+ydy+xzdz 解:设∑为平面z=y上被厂所围椭圆域,且取下侧, 则其法线方向余弦 cosy=- 1 cosa=0,cosB= , 2 利用斯托克斯公式得 cosa cos B cosy 品 品 8 ds-小0-)as-0 xy XZ
z 2 x y Γ O 例2. Γ 为柱面 与平面 y = z 的交线, 从 z 轴正向看为顺时针, d d d . 2 I = y x + xy y + xz z ∫Γ 解: 设Σ 为平面 z = y 上被 Γ 所围椭圆域 , 且取下侧, cosα = 0 , 利用斯托克斯公式得 I d S ∫∫ = Σ ∫∫ = − Σ ( y z)d S 21 = 0 则其法线方向余弦 , 2 1 cos β = 21 cosγ = − cosα cos β cosγ x y ∂ z ∂ ∂ ∂ ∂ ∂ y xy xz 2 x y 2y 2 2 + = Σ 计算