南阳师范学院：《高等数学》课程教学课件（同济第六版）第三章 微分中值定理与导数的应用 3.6 函数图形的描绘

第六节函数图形的描绘

第六节 函数图形的描绘

一、函数的渐近线 1.曲线的水平渐近线和垂直渐近线， 定义如果imf)=a(或1imfx)=a或1mfx)=a）, 那么称直线y=a为曲线y=fx的一条水平渐近线； 如果imfx)=∞（或imf)=或1mfx)=o), Y-h 那么称直线x=b为曲线y=f(x)的一条垂直渐近线

一、函数的渐近线 定义 如果 f x a x   lim ( ) (或 f x a x   lim ( ) 或 f x a x   lim ( ) ), 那么称直线 y  a为曲线 y  f (x)的一条水平渐近线; 如果    lim f (x) x b (或     lim f (x) x b 或     lim f (x) x b ), 那么称直线 x  b为曲线 y  f (x)的一条垂直渐近线. 1 .曲线的水平渐近线和垂直渐近线

二、函数作图 利用导数作函数图像的一般步骤如下： (1)确定函数的定义域； (2)研究函数的奇偶性、周期性； (3)讨论函数的单调性、极值、曲线的凹凸性及拐点，并列表； (4)确定曲线的水平渐近线和垂直渐近线； (5)根据作图需要适当选取辅助点； :(6)综合上述讨论，作出函数图像

二、函数作图 利用导数作函数图像的一般步骤如下 : (1) 确定函数的定义域; (2) 研究函数的奇偶性、周期性; (3) 讨论函数的单调性、极值、曲线的凹凸性及拐点,并列表; (4) 确定曲线的水平渐近线和垂直渐近线; (5) 根据作图需要适当选取辅助点; : (6) 综合上述讨论,作出函数图像

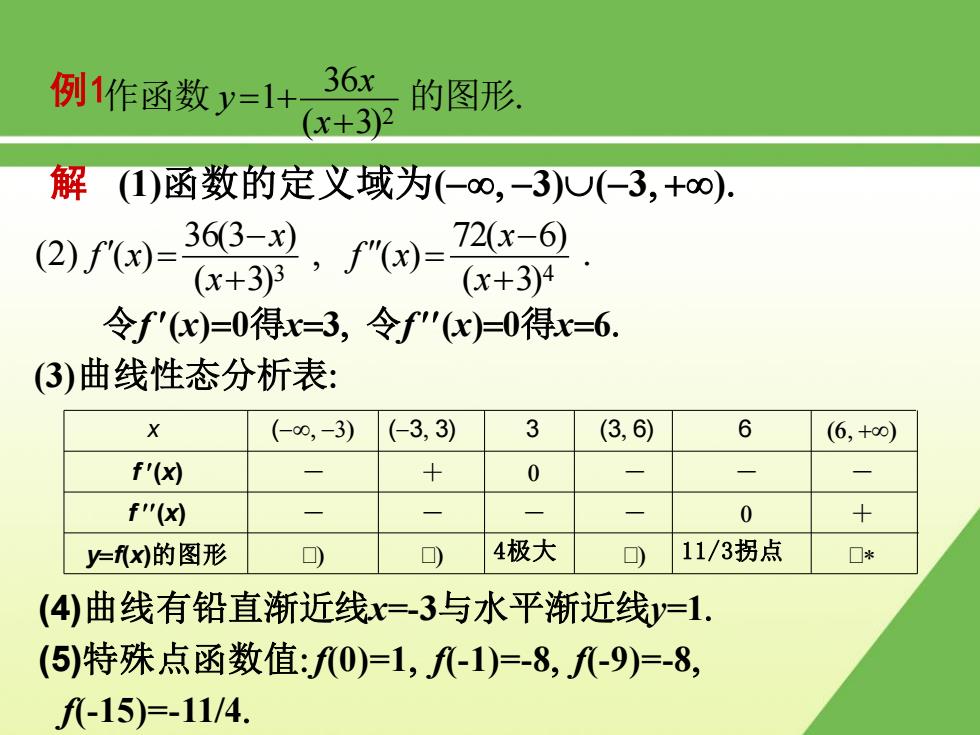
例1作函数y=1+ 36x 的图形 (x+3)2 解(1)函数的定义域为(-∞，-3)U(-3,+∞). (2)fx)= 363-x 2,)= 72(x-6) (x+3)3 (x+3)4 令f'c)=0得x=3,令f"'x)=0得x=6. (3)曲线性态分析表： X (-0,-3) (-3,3) 3 (3,6) 6 (6,+∞) f'(x刘 + 0 f"() 0 + y=x)的图形 口 0 4极大 0 11/3拐点 口* (4)曲线有铅直渐近线x=-3与水平渐近线y=1. (5)特殊点函数值：f0)=1,f八-1)=-8，f八-9)=-8， f-15)=-11/4

例 3 作函数 2 ( 3) 36 1    x x y 的图形 例1 解 (1)函数的定义域为( 3)(3 ) 令f (x)0得x3 令f (x)0得x6 (3)曲线性态分析表: x ( 3) (3 3) 3 (3 6) 6 (6 ) f (x) f (x) yf(x)的图形 － － － － － ＋ － － － 0 ＋ 0 ) ) 4极大 ) 11/3拐点  (4)曲线有铅直渐近线x=-3与水平渐近线y=1 (5)特殊点函数值:f(0)=1 f(-1)=-8 f(-9)=-8 f(-15)=-11/4 (2) 3 ( 3) 36(3 ) ( )     x x f x  4 ( 3) 72( 6) ( )     x x f x 

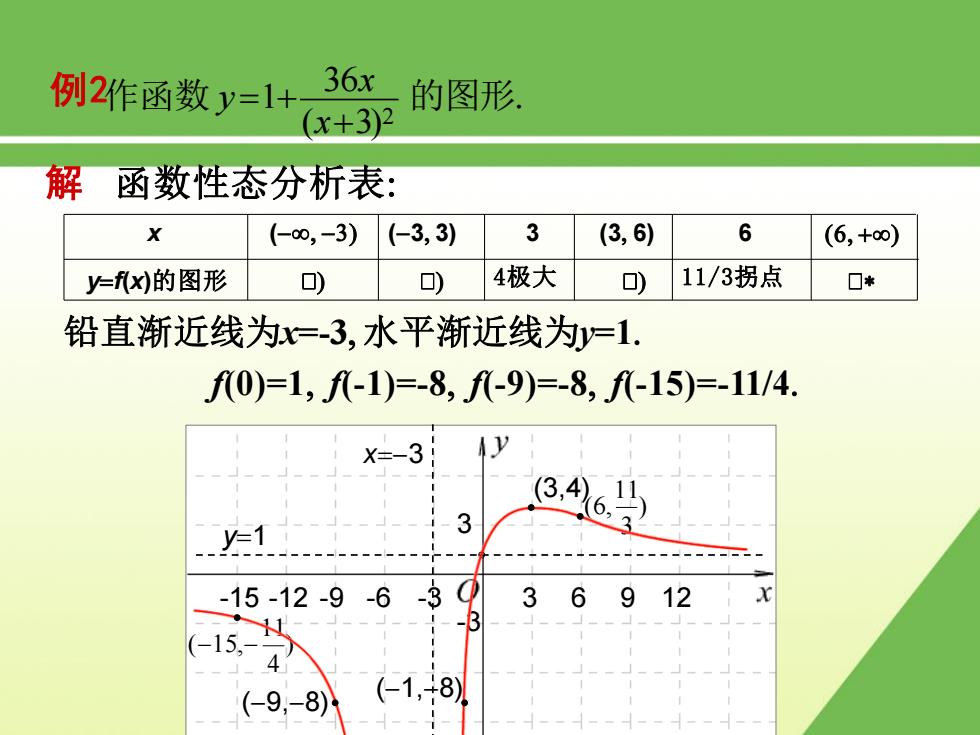
例2作函数y=1+ 36x 的图形. x+3)2 解函数性态分析表： (0,-3) （-3,3) 3 (3,6) 6 (6,+∞) y=fx)的图形 0) o) 4极大 可) 11/3拐点 ☐* 铅直渐近线为=3，水平渐近线为y=1. f0)=1,f-1)=-8,f-9)=-8,f-15)=-11/4. X=-3 (3,4)1 6 .y1 -15-12-9-6-30 36 912 -1 (-9,-8)1 (-1,+8)

-15 -12 -9 -6 -3 3 6 9 12 3 -3 x ( 3) (3 3) 3 (3 6) 6 (6 ) yf(x)的图形 ) ) 4极大 ) 11/3拐点  铅直渐近线为x=-3 水平渐近线为y=1 f(0)=1 f(-1)=-8 f(-9)=-8 f(-15)=-11/4 y1 x3 (3,4) ) 3 11 (6, (1,8) (9,8) ) 4 11 (15, 解 函数性态分析表: 例 3 作函数 2 ( 3) 36 1    x x y 的图形 例2