南阳师范学院：《高等数学》课程教学课件（同济第六版）第三章 微分中值定理与导数的应用 3.4 函数的单调性与凸凹性

第四节函数的单调性与凸凹性 基本内容 一、函数单调性的判定法 二、曲线的凹凸性与拐点

第四节 函数的单调性与凸凹性 一、函数单调性的判定法 二、曲线的凹凸性与拐点 基本内容

复习函数单调递增与单调递减的定义 设函数y=f)的定义域为D,区间IcD. (1)如果对于区间I上任意两点x1,2,当x,f(x2) 称函数fx)在区间I上是单调递减

复习函数单调递增与单调递减的定义 设函数 y  f(x)的定义域为 D, 区间 I D. （1）如果对于区间 I上任意两点 x1，x2 , 当 1 2 x  x 时, 恒有 称函数 f(x)在区间 I上是单调递增. ( ) ( ) 1 2 f x  f x （2）如果对于区间 I上任意两点 x1，x2 , 当 1 2 x  x 时, 恒有 1 2 f x f x ( ) ( )  称函数 f(x)在区间 I上是单调递减

函数单调性的判定法 函数y=孔x)的图象有时上升，有时下降.如何判断函数的图象 在什么范围内是上升的，在什么范围内是下降的呢？ 观察与思考 ) 函数的单调性与导数的符号 有什么关系？ •观察结果 函数单调增加时导数大于零， 函数单调减少时导数小于零： 0 a b

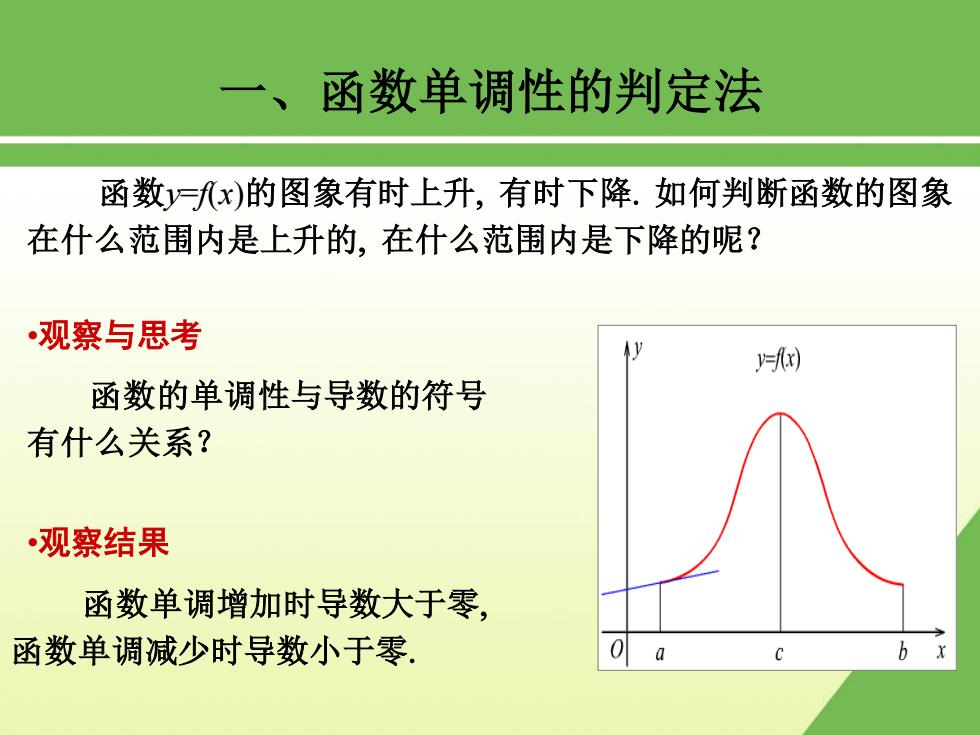
一、函数单调性的判定法 函数y=f(x)的图象有时上升, 有时下降. 如何判断函数的图象 在什么范围内是上升的, 在什么范围内是下降的呢？ •观察结果 函数单调增加时导数大于零, 函数单调减少时导数小于零. •观察与思考 函数的单调性与导数的符号 有什么关系？

定理1（函数单调性的判定法） 设函数fx)在4，b上连续，在(a,b)内可导. (1)如果在(a,b)内f)>0,则fx)在[a,b上单调增加； (2)如果在(a,b)内f'x)0,x2-x>0,所以 fx2)-fx1)=f'(x)c2-x1)>0, 即 fx)f,), 这就证明了函数fx)在4，b]内单调增加

定理1(函数单调性的判定法) 设函数f(x)在[a, b]上连续, 在(a, b)内可导. (1)如果在(a, b)内f(x)>0, 则f(x)在[a, b]上单调增加 (2)如果在(a, b)内f(x)0, x2 x1>0, 所以 f(x2 )f(x1 )f(x)(x2 x1 )>0, 即 f(x1 )<f(x2 ) , 这就证明了函数f(x)在[a, b]内单调增加. 证明: 只证(1). 在[a, b]内任取两点x1 , x2 (x1<x2 )

、】 函数单调性的判定法 2.判定定理的应用： (1)判断函数在某一区间上的单调性 证明函数在某区间上单调递增、单调递减 (2)求函数的单调区间 (3)证明不等式 (4)确定某些方程实根的个数

2 .判定定理的应用： （1）判断函数在某一区间上的単调性 （2）求函数的单调区间 （3）证明不等式 （4）确定某些方程实根的个数 证明函数在某区间上单调递增、单调递减 一、函数单调性的判定法

例1讨论函数y=e-x-1的单调性. 解函数y=e-x-1的定义域为-oo,o). y'=e-1. 因为在(-oo,0)内y'<0,所以函数y=-x-1在(-oo,0]上单调减 少； 因为在(0，+o)内y0,所以函数y=-x-1在[0，+oo)上单调增 加

因为在(, 0)内y0, 所以函数 ye xx1在[0, )上单调增 加. 解 函数ye xx1的定义域为(, ). ye x1. 例1 讨论函数 ye x x1的单调性

例2证明：当o1时，2>3-1 证明令fx)=2-(3-),则 因为当x>1时，f'x)>0,所以fx)在[1，+oo)上单调增加. 因此当x>1时，x)>f1)=0,即 y 2-6->0, y=2R-(3-) 也就是2>3-6o1 0 2

( 1) 1 1 1 ( ) 2 2     x x  x x x f x . 证明 令 ) 1 ( ) 2 (3 x f x  x   , 则 因为当x>1时, f (x)>0, 所以f(x)在[1, )上单调增加. 例 6. 证明 当 x1 时, x x 1 2 3 . 例2 证明 ) 0 1 2 (3  x x , 也就是 x x 1 2 3 (x1). 因此当x>1时, f(x)>f(1)=0, 即

例3讨论函数y=x2的单调性 解函数的定义域为(-oo,+oo). y=2(40,函数在0处不可导 3 因为x0时，y>0,所以函数在[0，+oo)上单调增加. 由该题我们得知： 在不可导点两侧，函数的 y=Vx2 单调性也可能发生改变

解 函数的定义域为(, ). 因为x>0时, y>0, 所以函数在[0, )上单调增加. 因为x<0时, y<0, 所以函数在(, 0] 上单调减少 例 例 3 3 . 讨论函数 3 2 y x 的单调性. 3 3 2 x y   (x0), 函数在 x0 处不可导. 由该题我们得知： 在不可导点两侧，函数的 单调性也可能发生改变

函数单调性的判定法 注记1：求单调区间的步骤 第一步：求出函数y=f(x)的定义域 第二步：求导数f"(x) 第三步：在定义区间内求出所有使f"(x)=0和使f"()不存在的点，并以这些 点为分界点，将定义域分为若干个子区间 第四步：（列表）判定f'(x)在每个区间上的正负号 第五步：利用判断定理得出递增及递减区间

注记 1：求单调区间的步骤 第一步：求出函数 y  f (x)的定义域 第二步：求导数 f x ( ) 第三步：在定义区间内求出所有使 f (x)  0和使 f (x)不存在的点, 并以这些 点为分界点,将定义域分为若干个子区间； 第四步：（列表）判定 f x ( )在每个区间上的正负号 第五步：利用判断定理得出递增及递减区间 一、函数单调性的判定法

2 例4讨论f(x)=(x-1)3的单调性 解 定义域为(-，+∞ x=x5±气c-Ie9S 5x-2 3无 2 田)0，解得x专 当x=0时，f(x)不可导. 列表如下： (-∞，0) 0 (0,2/5) 2/5 (2/5,+0) f'(x) + 不 0 + fx) 故函数在(-∞，0]和[25，+∞)递增，[0,2/5]递减。 注记4：单调区间的分界点除驻点外，也可能是导数不存在的点

解 定义域为(∞,+∞) f x ( )  3 5 - 2 3 x x  2 1 - 3 3 2 ( -1) 3 x x x  例4 讨论 的单调性 2 3 f x x x ( ) ( -1)  列表如下：    故 函数在(∞,0]和[2/5,+∞)递增，[0,2/5]递减。 f x ( ) x (-∞,0) 0 (0,2/5) 2/5 (2/5,+∞) f(x) 不 0 2 ( ) 0 5 令f x x    ，解得 ； 当x f x  0 ( ) 时， 不可导. 注记 4：单调区间的分界点除驻点外,也可能是导数不存在的点