
南阳师范学院一数学与统计学院 二、填空题(将正确答来填写在横战上) 《高等数学》第一章—函数与极限 1.若fx)=e,f(x)=1-x,则x)=」 练习题(A) 一、判断正误题(判断下列各愿是香正确,正确的划1,懒浅的划X) 之 )ia,i)={0<-d<d={a-6<x<au{a<x<a+8} () = (2)关系式x2-)2=1表示y是x的函数 () 4.liml= (3)关系式y=max{x,}+min{x,-l}表示y是x的函数 () 5.lim[(1+x+)(1-x+sinx)= (4)关系式y=ar心c0s业,u=2+x之表示y是x的函数 () (如》 6 5》若f)=gnx,则了=r0 () {0,x=0. 2 (6)若f(x)=lnx2,g(x)=2lnx,则fx)=g(x). () (7)y=in2x是周期为π的函数, () (8)imf5+A)=f)一lim(f,+A)-f》=0 9若imx,=a,则im- (9)y=0是曲线y=三的水平渐近线 () 10.若1imx,=a,则1im.= (10)y=f(x)在x连续的充要条件是f(x)=f(x)=f,)】 () (11)收敦数列的极限不唯一. () 北g. (12)limf(x)=A台fx)=A+a.(其中lima=0) () 8)m2=0 2品 () (14)设f(x),g(x在(-,+∞)内有定义.若f(x)连续且f(x)≠0,g(x)有间断 以岩 点则得有 () 第1页共3页
南阳师范学院—数学与统计学院 第 1 页 共 3 页 《高等数学》第一章-——函数与极限 练习题(A) 一、判断正误题(判断下列各题是否正确,正确的划√,错误的划×) (1) { } { } { } 0U a x x a xa x a xa x a (, ) 0 δ = < − < = −<< ∪ <<+ δδ δ ( ) (2)关系式 2 2 x y − =1表示 y 是 x 的函数 ( ) (3)关系式 yx x = +− max ,1 min , 1 { } { } 表示 y 是 x 的函数 ( ) (4)关系式 2 y = =+ arccos , 2 uu x 表示 y 是 x 的函数 ( ) (5)若 f ( ) sgn x x = ,则 2 1, 0, ( ) 0, 0. x f x x ⎧ ≠ = ⎨⎩ = ( ) (6)若 2 f ( ) ln , ( ) 2ln , x x gx x = = 则 f () () x gx = . ( ) (7) 2 y = sin x 是周期为π 的函数. ( ) (8) 0 0 00 ( ) 0 0 lim ( ) ( ) lim ( ) ( ) 0 x x fx x fx fx x fx Δ→ Δ→ +Δ = ⇔ +Δ − = . ( ) (9) y = 0是曲线 21 y x = 的水平渐近线. ( ) (10) y = f x( ) 在 0 x 连续的充要条件是 000 f ( ) ( ) () x fx fx − + = = . ( ) (11)收敛数列的极限不唯一. ( ) (12)lim ( ) ( ) . fx A fx A =⇔ =+α (其中lim 0 α = ). ( ) (13) 2 1 2 lim 0 n n →+∞ n + +⋅⋅⋅+ = ( ) (14)设 f ( ) x , g x( ) 在(, ) −∞ +∞ 内有定义.若 f ( ) x 连续且 f x() 0 ≠ , g x( ) 有间断 点,则 ( ) ( ) g x f x 必有间断点 ( ) 二、填空题(将正确答案填写在横线上) 1. 若 ( ) , ( ( )) 1 , x f x ef x x = ϕ = − 则ϕ( ) x = 2. 2 arctan lim n n →+∞ n = 3. 2 1 2 lim 10n n→+∞ n ⎛ ⎞ ⎜ ⎟ + = ⎝ ⎠ 4. 0 lim x x → = 5. ( )( ) 2 2 0 lim 1 1 sin x xx x x → ⎡ + + −+ =⎤ ⎣ ⎦ 6. 2 21 lim sin n n →+∞ n ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ 7. 2 lim 3 1 n n→+∞ n ⎛ ⎞ ⎜ ⎟ − = ⎝ ⎠ 8. ( )3 0 sin 2 lim x tan x → x = 9. 若 lim , n n x a →∞ = 则 lim n n x →∞ = 10. 若 lim , n n x a →∞ = 则 2 lim n n x →∞ = 11. ( )2 2 0 lim h x h x → h + − = 12. 2 3 1 lim x 1 x →∞ x − = + 13. 3 3 1 lim x 1 x →∞ x + = −

南阳师范学院一数学与统计学院 三、选择题(将正确答案的序号填写在括号内) D:m)存在的充要条件是函数)在点处的左右极限存在且相等 (1)设函数f(x)的定义域为D,数集X∈D,则下列命题错误的是() 玉若函数在点处的左右极限存在包不相等,则回 一定存在 A:若f(x)在X上有界,则f(x)在X上既有上界也有下界 (6)若mf(x)=0,img(x)=oo,则下列结论错误的是() B:若fx)在X上有界,则f(x在X上也有界 A:Iim(f(x)±gx)不存在 B:im(f(xg(x)不一定存在 C着因在X上有界,则而在X上逸无界 C:lim[2fx】一定存在 D:m但不存在 g(x) D:若(x在X上无界,则fx)在X上也无界 (7)下列结论正确的是() (2)下列结论错误的是() A:绝对值很小的数一定是无穷小B:至少有两个常数是无穷小 A:y=sinx在定文域上有界B:y=anx在定义域上有界 C:常数不可能是无穷小D:在自变量的某一变化过程中,趋向0的函数是无穷小 C:y=arctanx在定义域上有界D:y=arccosx在定义域上有界 (8)下列结论正确的是( (3)下列结论正确的是() A:有界函数与无穷大的积不一定为无穷大 B:无限个无穷小的和仍为无穷小 A:y=arcsinx的定义域是(-o,+) B:y=arctanx的值t域是(-e,+o) C:两个无穷大的和(积及商)仍为无穷大 D:无界函数一定是无穷大 C:y=c0sx的定义域是(-丸,+o) D:=acem玉的值城是(仁受受 (9)下列等式不成立的是( (4)若1imx。=a,则下列结论错误的是() 心=六0 1 Bs恤n+D0 A:{x}必有界 c:lim2”"=+o D:lim (vn+1-)=1 C:必有lim.=im=a D:必有imxo+loo=a (10)下列结论错误的是() (5)下列结论正确的是() A:单调有界数列必收敛 B:单增有上界的数列必收敛 A:若函数f)在点x,处的左右极限存在,则1mf)一定存在 C:单调数列必收敛 D:单减有下界的数列必收敛 B:若函数f()在点处无定义,则1imf(x)一定不存在 (11)下列结论正确的是〔) C:若mfx)不存在,则必有m)=0 A:当x→0时,e2-1是比之高阶的无穷小 B:当x→1时,x-1与x产-1是同阶的无穷小 第2页共3页
南阳师范学院—数学与统计学院 第 2 页 共 3 页 三、选择题(将正确答案的序号填写在括号内) (1)设函数 f ( ) x 的定义域为 D ,数集 X ⊂ D ,则下列命题错误的是( ) A:若 f ( ) x 在 X 上有界,则 f ( ) x 在 X 上既有上界也有下界 B:若 f ( ) x 在 X 上有界,则 f ( ) x 在 X 上也有界 C:若 f ( ) x 在 X 上有界,则 1f ( ) x 在 X 上必无界 D:若 f ( ) x 在 X 上无界,则 f ( ) x 在 X 上也无界 (2)下列结论错误的是( ) A: y = sin x 在定义域上有界 B: y = tan x 在定义域上有界 C: y = arctan x 在定义域上有界 D: y x = arccos 在定义域上有界 (3)下列结论正确的是( ) A: y = arcsin x 的定义域是(, ) −∞ +∞ B: y = arctan x 的值域是(, ) −∞ +∞ C: y x = cos 的定义域是(, ) −∞ +∞ D: y = arc x cot 的值域是( ,) 2 2 π π − (4)若 lim n n x a →+∞ = ,则下列结论错误的是( ) A:{ }n x 必有界 B:必有 1 1 lim n n →∞ x a = C:必有 2 21 lim lim n n n n x x a − →∞ →∞ = = D:必有 1000 lim n n x a + →∞ = (5)下列结论正确的是( ) A:若函数 f ( ) x 在点 0 x 处的左右极限存在,则 0 lim ( ) x x f x → 一定存在 B:若函数 f ( ) x 在点 0 x 处无定义,则 0 lim ( ) x x f x → 一定不存在 C: 若 0 lim ( ) x x f x → 不存在,则必有 0 lim ( ) x x f x → = ∞ D: 0 lim ( ) x x f x → 存在的充要条件是函数 f ( ) x 在点 0 x 处的左右极限存在且相等 E:若函数 f ( ) x 在点 0 x 处的左右极限存在但不相等,则 0 1 lim ( ) x x → f x 一定存在 (6)若 lim ( ) 0, lim ( ) x x f x gx →∞ →∞ = =∞,则下列结论错误的是( ) A: lim ( ) ( ) ( ) x f x gx →∞ ± 不存在 B: lim ( ) ( ) ( ) x f xgx →∞ 不一定存在 C: lim[2 ( )] x f x →∞ 一定存在 D: ( ) lim ( ) x f x →∞ g x 不存在 (7)下列结论正确的是( ) A:绝对值很小的数一定是无穷小 B:至少有两个常数是无穷小 C:常数不可能是无穷小 D:在自变量的某一变化过程中,趋向 0 的函数是无穷小 (8)下列结论正确的是( ) A:有界函数与无穷大的积不一定为无穷大 B:无限个无穷小的和仍为无穷小 C:两个无穷大的和(积及商)仍为无穷大 D:无界函数一定是无穷大 (9)下列等式不成立的是( ) A: 1 lim 0 2n n→+∞ n = B: 1 lim 0 ln( 1) n→+∞ n = + C: lim 2n n→+∞ = +∞ D: lim 1 1 ( ) n n n →+∞ +− = (10)下列结论错误的是( ) A:单调有界数列必收敛 B:单增有上界的数列必收敛 C:单调数列必收敛 D:单减有下界的数列必收敛 (11)下列结论正确的是( ) A:当 x → 0时, 1 x e − 是比 2 x 高阶的无穷小 B:当 x →1时, x−1与 2 x −1是同阶的无穷小

南阳师范学院一数学与统计学院 C当n一中时.子是比片低阶的无方小 (17)下列结论错误的是() D:当x+0时,若sinr~tnx,则a=2 A:∈(-,+o,m sinx=sin B:limInsinx=0 (12)下列结论不正确的是( C.,).lim arccosx=arccos D:msgnxsgn 0是/了S=日的跳跃间斯点B:号是 的可去间断点 四、计算愿 tanx C:f(x)=cotx只有一个间断点 D:x=0是f)=simn上的第二类间断点 1.lim arcsin 品 (13)下列结论不正确的是() s 4ml+3amn2产 A若im名=a,则imo=a 益 5.lim. -”1 五、证明题 C着0气片则m=0 (1)下列数列收敛的是() 1.证明函数f(x)= 在点x=0处连续. x>0 A:1-ll…,(-l sin I B:2,48…,2”,… x c是 僩 2.证明f八x)= 0 (sinx 在定义域内连续的充要条件是a=1, a+r',xs0 (15)下列数列发散的是() 3.设f(x)在0,上连续,且f0)=0,f)=1,证明存在5∈(0,),使得f()=1-5 A如受 B=旷片 4证明四本2叶+a0 1 1 c54日 D:x.=n(-1)" (16)下列变量在给定变化过程中,不是无穷大量的是() 5.设fx)在0,2]上连续,且f0)+f0+f2)=3,求证:存在5e0,2],使f八)=1 A:gx,(x→0) B:lgx,(x→+o) 6.证明方程x-3x=1在1与2之间至少存在一个实根. C:x2+l,(x→0) D:e,x→0) 第3页共3页
南阳师范学院—数学与统计学院 第 3 页 共 3 页 C:当 n → +∞ 时, 21 n 是比 1 n 低阶的无穷小 D:当 x → 0时,若sin tan ax x ∼ ,则 a = 2 (12)下列结论不正确的是( ) A: x = 0 是 ( ) x f x x = 的跳跃间断点 B: 2 x π= 是 ( ) tanx f x x = 的可去间断点 C: f ( ) cot x x = 只有一个间断点 D: x = 0 是 1 f x( ) sin x = 的第二类间断点 (13)下列结论不正确的是( ) A:若 lim , n n x a →+∞ = 则 10 lim n n x a + →+∞ = B: 0 1 lim 1 tan x x e → x − = C:若 1 0 nx n ≤ xx 在点 x = 0处连续. 2. 证明 2 sin , 0 ( ) , 0 x x f x x ax x ⎧⎪ > = ⎨⎪ + ≤ ⎩ 在定义域内连续的充要条件是 a =1. 3. 设 f ( ) x 在[0,1] 上连续,且 f (0) 0 = , f (1) 1 = ,证明存在ξ ∈(0,1) ,使得 f () 1 ξ = −ξ . 4. 证明 22 2 11 1 lim 0 n→∞ n n nn 1 2 ⎛ ⎞ ⎜ ⎟ + +⋅⋅⋅+ = ⎝ ⎠ ++ + . 5. 设 f ( ) x 在[0, 2]上连续,且 f ff (0) (1) (2) 3 + + = ,求证:存在ξ ∈[0, 2],使 f () 1 ξ = . 6. 证明方程 5 x − 3 1 x = 在1与2 之间至少存在一个实根

南阳师范学院—一数学与统计学院 x+a,x>0 《高等数学》第一章-—函数与极限 (14)fx)={0, x=0在x=0连续的充要条件是a=0 () x-a,x≥0 (20)mP42+r.0 (8)函数f(x)=cos4x的反函数f(x)=arccos4x () n (9)若fx)=V(sgnx),g(x)=sgnx,则f)=g(x). () 二、填空题(将正确答寒填写在横线上) (10)y=sin2x+tam于是周期为x的函数 () 1.若fx)=e,f(op(x)》=1-x,则gx)= ()函数y=√一7,u=gx能构成复合函数y=√-g云的充分必要条件是 2.Jim 4arctan(n-lY(sinn+1 n2-100 x∈l,10] () =台+品} 3. (12)曲线y=e云的水平渐近线是y=1 () 4.mk-小sgnr-= (13)若1mf田不存在,则必有f红)≠f八。) () 5.m+2 第1页共4页
南阳师范学院——数学与统计学院 第 1 页 共 4 页 《高等数学》第一章---函数与极限 练习题(B) 一、判断正误题(判断下列各题是否正确,正确的划√,错误的划×) (1) 2 xx x − − 是偶函数 ( ) (8)函数 f ( ) cos 4 x x = 的反函数 1 f ( ) arccos 4 x x − = ( ) (9)若 2 f ( ) (sgn ) , ( ) sgn , x x gx x = = 则 f () () x gx = . ( ) (10) sin 2 tan 2 x y x = + 是周期为π 的函数. ( ) (11)函数 2 y =− = 1 , lg uu x 能构成复合函数 2 y = −1 lg x 的充分必要条件是 x∈[1,10] ( ) (12) 曲线 2 1 x 1 y e − − = 的水平渐近线是 y =1 ( ) (13) 若 0 lim ( ) x x f x → 不存在,则必有 0 0 f () () x fx − + ≠ ( ) (14)) , 0 ( ) 0, 0 , 0 xa x f x x xa x ⎧ + > ⎪ = ⎨ = ⎪⎩ − < 在 x = 0 连续的充要条件是 a = 0 ( ) (15)设 f ( ) x , g x( ) 在 (, ) −∞ +∞ 内有定义, f ( ) x 为连续,且 f x() 0 ≠ ,若 g x( ) 有间断 点,则 2 2 2 () ( ) g x f x 必有间断点 ( ) (16) x =1是函数 ( )2 y x = sgn( 1) 1 − + 的可去间断点 ( ) (17) 4 x π = 是 2 y = tan 2 1 x − 的无穷间断点 ( ) (18)lim ( ) 1 ( ) 1 . fx fx = ⇔ =+α (其中lim 0 α = ) () (19) 20 80 100 ( 1) ( 100) lim 1 ( 1) n n n →∞ n − + = + ( ) (20) 22 2 2 1 2 lim 0 n n →+∞ n + +⋅⋅⋅+ = ( ) 二、填空题(将正确答案填写在横线上) 1. 若 ( ) , ( ( )) 1 , x f x ef x x = ϕ = − 则ϕ( ) x = 2. 2 4arctan( 1)(sin 1) limn 100 n n →+∞ n − + = − 3. 4 1 7 lim 100n n→+∞ n ⎛ ⎞ ⎜ ⎟ + = ⎝ ⎠ 4. ( ) 1 lim 1 sgn( 1) x x x → − − = 5. 2 2 3 0 1 lim (3 cos ) x 2 x x → x ⎡ + ⎤ + = ⎢ ⎥ ⎣ + ⎦

南阳师范学院—数学与统计学院 &-(rm引 一'()在(-,+)上也是单调递增且连线 =- D话数=cex的定义线为(-树,值越为(-受引 (2)下列数列收敛的是() 《品侣部 A:x。:l-l,l,-l1-l… 9.若m=a,则1m.+4们- B:xn:0,12,3,4,5… C:x :0,In2,In3,In4,In5,... L画任+之。 (3)下列数列发散的是() h 斗信 13.limInsinx= (4)下列结论错误的是() A:单调有界数列必收敛 n 14.ln cosx B:发散的数列必无界 C:数列收敛的充要条件是任意子列都收敛于同一个数 三、选择题(将正确答来的序号填写在括号内) D:收效的数列必有界 (1)下列结论错误的是() (s)若Iimf(x)与1img(x)都不存在,则( A:由于函数f)=simx在习上单调递增,因此f代)的反函数厂) 多存在且了广国)的定文线-山小、值城受引 A:lim[/(x)+g(x与im[f(xg(ax都不存在 B:lim[f(x)+g(x与lim[f(x)g(x一定都存在 B:在同一平面坐标系中,函数y=fx)与其反函数y=(x)的图形关于直线 y=x对称 c.imf(-)g到与im]s不存在 Lg()] C由于函数f)=mr在-受,上单调递增且连续。因此f:)的反函数 第2页共4页
南阳师范学院——数学与统计学院 第 2 页 共 4 页 6. 2 4 2 lim sin n n →+∞ n ⎛ ⎞ ⎜ ⎟ = ⎝ ⎠ 7. 2 4 lim 10 1 n n→+∞ n ⎛ ⎞ ⎜ ⎟ − = ⎝ ⎠ 8. ( )100 50 0 sin 4 lim (tan 2 ) x x → x = 9. 若 lim , n n x a →+∞ = 则 2 21 lim n n n x x − →+∞ ⎡ + ⎤= ⎣ ⎦ 10. 2 2 5 limx 2 x → x − = − 11. ( )3 3 0 limh x h x → h + − = 12. 200 1000 1 limx 1 x →∞ x − = + 13. 2 lim ln sin x x π → = 14. 2 0 1 lim cos x x e → x − = 三、选择题(将正确答案的序号填写在括号内) (1)下列结论错误的是( ) A:由于函数 f ( ) sin x x = 在[ ,] 2 2 π π − 上单调递增,因此 f ( ) x 的反函数 1 f ( ) x − 必存在且 1 f ( ) x − 的定义域为[ 1,1] − ,值域为[ ,] 2 2 π π − B:在同一平面坐标系中,函数 y = f x( ) 与其反函数 1 y f x( ) − = 的图形关于直线 y = x 对称 C:由于函数 f ( ) tan x x = 在 , 2 2 ⎛ ⎞ π π ⎜ ⎟ −⎝ ⎠上单调递增且连续,因此 f ( ) x 的反函数 1 f ( ) x − 在(−∞ +∞ , ) 上也是单调递增且连续. D:函数 f ( ) cot x arc x = 的定义域为(, ) −∞ +∞ ,值域为 , 2 2 ⎛ ⎞ π π ⎜ ⎟ −⎝ ⎠ (2)下列数列收敛的是( ) A: :1, 1,1, 1,1, 1, n x − − − " B: : 0,1, 2,3, 4,5, n x " C: : 0,ln 2,ln 3,ln 4,ln 5, n x " D: 111 : 0, , 0, , 0, , 248 n x " (3)下列数列发散的是( ) A: ( 1) 1 n n ⎧ − + ⎫ ⎨ ⎬ ⎩ ⎭ B: 3 1 10n ⎧ ⎫ ⎨ + ⎬ ⎩ ⎭ C: {( 2) } n − D: 1 n n ln( 1) ⎧ ⎫ ⎨ ⎬ ⎩ ⎭ + (4)下列结论错误的是( ) A:单调有界数列必收敛 B:发散的数列必无界 C:数列收敛的充要条件是任意子列都收敛于同一个数 D:收敛的数列必有界 (5)若lim ( ) f x 与lim ( ) g x 都不存在,则( ) A:lim ( ) ( ) [ f x gx + ] 与lim ( ) ( ) [ f xgx ]都不存在 B:lim ( ) ( ) [ f x gx + ] 与lim ( ) ( ) [ f xgx ]一定都存在 C:lim ( ) ( ) [ f x gx − ] 与 ( ) lim ( ) f x g x ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ 都不存在

南阳师范学院—一数学与统计学院 D:liml/e)±gx小、lim/sgx与limg 可能存在。也可能不存在 A: B:x C:x D:x (1l)设当x一→0时,tanx-sinx是比arcsin”x高阶的无穷小,则正整数n等于() (6)下列结论正确的是( A:1或2B:4C:5D:3 A:若imf四)>lim.则必有f)>gx) (12)设a(x)=e-l,x)=n(x+,m,n∈N,则当x→0时,下列结论正确的是( B:若f)>g国,则必有im)>1im田 A:当m>n时,(x)必是x)等价的无穷小 C若四f=4则f田必有界 B:当m=n时,a(x)必是B(x)高阶的无穷小 D:mf田=4的充要条件是对任意数列工,→,火。→,有 C:当m<n时,a(x)是(x)的低阶无穷小 im f)=limn f()=4 D:当m<n时,a(x)是(x)的同阶无穷小 (7)下列结论正确的是() (13)设若a~',B~B,则下列结论可能不正确的是( A:若数列x无界,则数列x,一定发敬 A:aB~a'B' B:a±B~x±B B:若ma.=0,m6,=L则m么一定存在 C:a/B-a'lB' D:Ca~Ca'C¥0) a. C:若1imk=,则必有lim=a 14)f)-H 在x=0有() D:若1imn=imx4=a,则im不一定不存在 A:跳跃间断点 B:可去间断点 (8)当x→+0时,下列变量中不是无穷小量的是() C:震荡间断点 D:无穷间断点 x-1 1 A:2++ B:vx2+1 15》函数严-丽的同断在有() A:1个: B:2个 C:3个D:4个 C: 0-)sim之 T n子m x+:+cx则a,6c的值一定为() 1 1 (9)下列变量在给定的变化过程中为无穷大量的是( (16)当x→0o时,若 A:xsn(x→0) B:上sin2xG→0) A:a=0,b=Lc=-1 B:a=0,b=L,c为任意常数 C:xcosx (xoo) D.cos (0) C:a=0,b,c为任意常数 D:a,b,c为任意常数 (10)当x→0时,下列变量中与anx为等价无穷小量的是() (17)下列极限中结果等于e的是() 第3页共4页
南阳师范学院——数学与统计学院 第 3 页 共 4 页 D:lim ( ) ( ) [ f x gx ± ] 、 lim ( ) ( ) [ f xgx ]与 ( ) lim ( ) f x g x ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ 可能存在,也可能不存在 (6)下列结论正确的是( ) A:若 0 0 lim ( ) lim ( ) xx xx f x gx → → > ,则必有 f () () x gx > B:若 f () () x gx > ,则必有 0 0 lim ( ) lim ( ) xx xx f x gx → → > C:若 0 lim ( ) , x x f x A → = 则 f ( ) x 必有界 D: 0 lim ( ) x x f x A → = 的充要条件是对任意数列 0 0 , , n n x → → xy x 有 0 0 lim ( ) lim ( ) n n n n xx yx f x fy A → → = = (7)下列结论正确的是( ) A:若数列 n x 无界,则数列 n x 一定发散 B:若 lim 0, lim 1, n n n n a b →∞ →∞ = = 则 lim n n n b →∞ a 一定存在 C:若 lim n n x a →+∞ = ,则必有 lim n n x a →+∞ = D:若 2 21 lim lim n n n n x x a − →+∞ →+∞ = = ,则 lim n n x →+∞ 一定不存在 (8)当 x → ∞时,下列变量中不是无穷小量的是( ) A: 3 2 1 1 x x x − + + B: 2 x +1 C: 2 2 1 (1 ) sin 1 x x x − − D: 2 2 1 1 sin 1 x x x − − (9)下列变量在给定的变化过程中为无穷大量的是( ) A: 4 1 x x sin ( 0) x → B: 1 2 sin ( 0) x x x → C: x xx cos ( ) → ∞ D: 1 cos ( 0) x x x → (10)当 x → 0时,下列变量中与 2 tan x 为等价无穷小量的是( ) A: x B: x C: 2 x D: 3 x (11)设当 x→0 时, tan sin x − x 是比 sinn arc x 高阶的无穷小,则正整数 n 等于( ) A:1 或 2 B:4 C:5 D:3. (12)设 ( ) 1, ( ) ln( 1), , mx n α β x e x x mn N+ =− = + ∈ ,则当 x→0 时,下列结论正确的是( ) A:当 m n > 时,α( ) x 必是 β ( ) x 等价的无穷小 B: 当 m n = 时,α( ) x 必是 β ( ) x 高阶的无穷小 C:当 m n < 时,α( ) x 是 β ( ) x 的低阶无穷小 D:当 m n < 时, α( ) x 是 β ( ) x 的同阶无穷小 (13)设若α ∼ ∼ αβ β ′, ,′ 则下列结论可能不正确的是( ) A:αβ αβ ∼ ′ ′ B: α ± ± βα β ∼ ′ ′ C:α β αβ ∼ ′ ′ D: C CC α ∼ α′( 0) ≠ (14) ( ) x f x x = 在 x = 0 有( ) A:跳跃间断点 B:可去间断点 C:震荡间断点. D:无穷间断点 (15)函数 1 ( 3)ln y x x = − 的间断点有( ) A:1 个; B:2 个 C:3 个 D: 4 个 (16)当 x → ∞时,若 2 1 1 ax bx c x 1 ∼ ++ − ,则 abc , , 的值一定为( ) A: a bc = 0, 1, 1 = =− B: a bc = = 0, 1, 为任意常数 C: a bc = 0, , 为任意常数 D: abc , , 为任意常数 (17)下列极限中结果等于e 的是( )

南阳师范学院—数学与统计学院 人产产 5.求imn-nn+) c D:l细+tamx w质数-古在在1装(, 五、讨论题 0x=1 sin'x 1.讨论fx)= 工心在定义域内的连线性 A:连续 B:不连续,但右连续或有右极限 x+l, x=0. C:不连续,但左连续或有左极限D:左、右都不连续 sin xarceos (19)下列结论正确的是() x x>0; 2.讨论a取何值可使fx)=0, x=0,在定义域内连续 A:若函数f(x)在(a,b)内连续,则f(x)在(a,b)内一定有界 In(1-x)+a,x0.证明存在5∈(0,).使f(5)=1-5 连续,则复合函数y=几x月在点x=x处也是连续的 D:一切初等函数在其定义域内都是连续的 2回南本小 四、计算题 3.设fx)在0,2】上连续,且f(0)+f0)+f2)=3,求证:存在5∈0,2.使f(5)=1 1我四-名0 求f(x)在x=0的极限 4.证明曲线y=x-3x2+7x-10在x=1与x=2之间至少存在与x轴有一个交点 2求▣acmF+x- 5.证明p>0时,函数fx)= 5 x0 x≤0在点x=0处连线 0. x=0 x>0 x I 3.求细一- 6.证明:nf田=A白f国=A+a,其中ma=0. (1+2-1)arcsinx 4求明 tanx? 第4页共4页
南阳师范学院——数学与统计学院 第 4 页 共 4 页 A: sin 0 sin 2 lim 1 x x x x → x ⎛ ⎞ ⎜ ⎟ + ⎝ ⎠ B: sin sin lim 1 x x x x →∞ x ⎛ ⎞ ⎜ ⎟ − ⎝ ⎠ C: sin sin lim 1 x x x x x − →∞ ⎛ ⎞ ⎜ ⎟ − ⎝ ⎠ D: ( )2cot 0 lim 1 tan x x x → + (18)函数 1 1 1 ( ) 0 1 x e x f x x − − ⎧⎪ ≠ = ⎨⎪⎩ = 在点 x =1处( ) A:连续 B:不连续,但右连续或有右极限 C:不连续,但左连续或有左极限 D:左、右都不连续 (19)下列结论正确的是( ) A:若函数 f ( ) x 在(,) a b 内连续,则 f ( ) x 在(,) a b 内一定有界 B:若函数 f ( ) x 在[,] a b 内有间断点,则 f ( ) x 在[,] a b 上一定没有最值 C:若函数u x = ϕ( ) 在点 0 x = x 处连续,且 0 0 ϕ( ) x = u ,而函数 y = f u( ) 在点 0 u u = 处 连续,则复合函数 y = f x [ ( )] ϕ 在点 0 x = x 处也是连续的 D:一切初等函数在其定义域内都是连续的 四、计算题 1.设 ( ) 0. 1 0 x e x f x x ⎧ ≤ = ⎨⎩ > 求 f (x) 在 x = 0 的极限 2.求 2 1 lim arctan x x x x →+∞ + − 3.求 3 2 1 1 lim( ) x 1 1 x → x x − − − 4. 求 ( )2 0 1 2 1 sin limx tan x arc x → x + − 5. 求 lim ln( 1) ln( 1) n n n →∞ n n ⎛ ⎞ ⎜ ⎟ − ⎝ ⎠ − + 五、讨论题 1. 讨论 2 sin , 0; ( ) 1, 0. x x f x x x x ⎧⎪ ≠ = ⎨⎪⎩ + = 在定义域内的连续性 2. 讨论 a 取何值可使 1 sin arccos , 0; ( ) 0, 0; ln(1 ) , 0. x x x fx x xa x ⎧ > ⎪⎪ = = ⎨⎪ − + ,证明存在ξ ∈(0,1) ,使ξ f () 1 ξ ξ = − 2. 证明 22 2 11 1 lim 1 1 2 n n n nn →∞ ⎛ ⎞ ⎜ ⎟ + +⋅⋅⋅+ = ⎝ ⎠ ++ + 3. 设 f ( ) x 在[0, 2]上连续,且 f ff (0) (1) (2) 3 + + = ,求证:存在ξ ∈[0, 2],使 f () 1 ξ = 4. 证明曲线 4 2 yx x x = − +− 3 7 10在 x =1与 x = 2之间至少存在与 x 轴有一个交点 5. 证明 p > 0时,函数 1 sin , 0 ( ) 0, 0 p x x f x x x ⎧⎪ ≠ = ⎨⎪⎩ = 00 >≤ xx 在点 x = 0处连续. 6. 证明: 0 lim ( ) ( ) x x fx A fx A α → = ⇔ =+ ,其中 0 lim 0 x x α → =
南阳师范学院一数学与统计学院 《高等数学》第一章—函数与极限 二.单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码填在题干上 自测题(A) 的话号内.每小题2分,共10分) 题号 三 四 六 总分 1若!mf)=0x)≠0),m8)=1,则下列结论不一定正确的是() 得分 受网如 B:g2f产()+gx=1 一判断题(判断下列各题是否正确,正确的划,错误的划×.每小题2分,共24分) 1数列+是收敛数列,数列-少是发散数列. c=儡0 D:f(x)>g(x) () 2.若m.≠m5则数列{}发散 () 2.下列结论不正确的是() 3.mf到=Aof)=A+a,(其中ma=0) () 学 B:lim(sininx)=1 4无限个无穷小量之和仍为无穷小量. () 5.无界量一定是无穷大量. () c:l+x炉=e ,sim9=0 D:。x 6若职=%则吗石0, () 3.函数fx)=emr不是() 7.一切初等函数在其定义区间内都是连续的, () A:偶函数 B:单调函数 8.若a~c,B~B,则必有a+B~r'+B () C:有界函数 D:周期函数 9.当x→0时,e-1是比x高阶的无穷小量 () 4.设函数f(x)在Ia,b1上连续,则下列结论错误的是( A:fx)在Ia,b上有界 10.y=x+arcsinx在[-l,】上是单调递增的. () 11.函数fx)=上是x→助时的无穷小量 B:fx)在a,b]上必有最大值和最小值 () T C:若fa)f(b)<0,则至多有一点a<5<b),使f()=0 业 () D:若f(a)<C<fb),则至少有一点(a<5<b)·使f)=C 第1页共2页
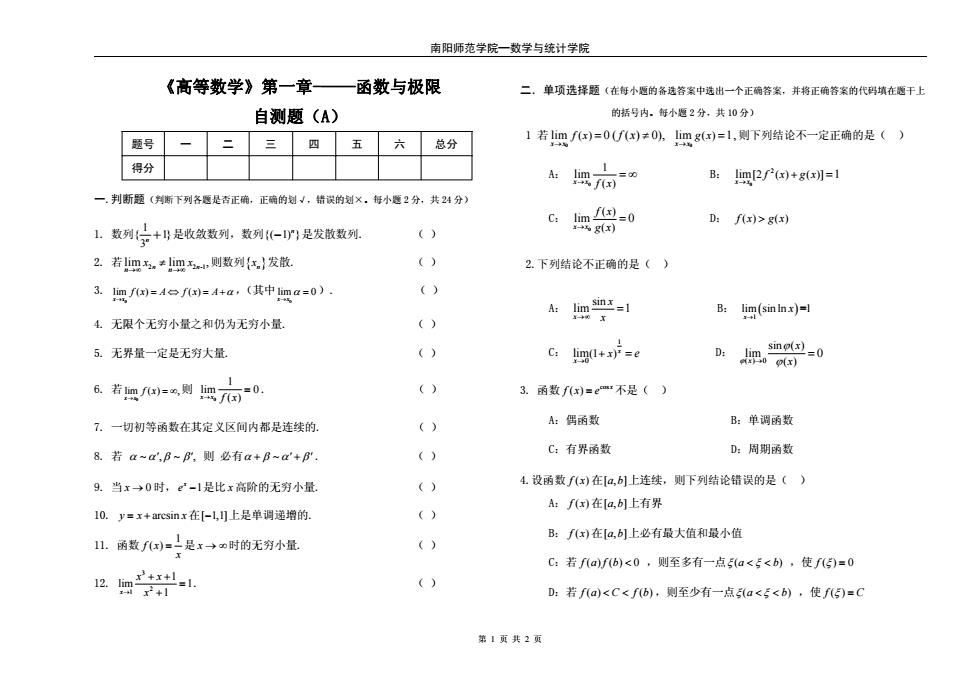
南阳师范学院—数学与统计学院 第 1 页 共 2 页 《高等数学》第一章-——函数与极限 自测题(A) 题号 一 二 三 四 五 六 总分 得分 一.判断题(判断下列各题是否正确,正确的划√,错误的划×。每小题 2 分,共 24 分) 1. 数列 1 { 1} 3n + 是收敛数列,数列{( 1) }n − 是发散数列. ( ) 2. 若 2 2 -1 lim lim , n n n n x x →∞ →∞ ≠ 则数列{xn}发散. ( ) 3. 0 lim ( ) ( ) x x fx A fx A α → =⇔ =+ ,(其中 0 lim 0 x x α → = ). ( ) 4. 无限个无穷小量之和仍为无穷小量. ( ) 5. 无界量一定是无穷大量. ( ) 6. 若 0 lim ( ) , x x f x → = ∞ 则 0 1 lim 0 ( ) x x → f x = . () 7. 一切初等函数在其定义区间内都是连续的. ( ) 8. 若 α ∼ ∼ αβ β ′ ′ , , 则 必有α + + βα β ∼ ′ ′ . () 9. 当 x → 0 时, 1 x e − 是比 x 高阶的无穷小量. ( ) 10. yx x = + arcsin 在[ 1,1] − 上是单调递增的. ( ) 11. 函数 1 f x( ) x = 是 x → ∞时的无穷小量. ( ) 12. 3 2 1 1 lim 1 x 1 x x → x + + = + . () 二.单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码填在题干上 的括号内。每小题 2 分,共 10 分) 1 若 0 lim 0 ( ( ) 0), ( ) x x f x f x → = ≠ 0 lim 1, ( ) x x g x → = 则下列结论不一定正确的是( ) A: 0 1 ( ) lim x x → f x = ∞ B: 0 2 lim 1 [2 ( ) ( )] x x f x gx → + = C: 0 ( ) ( ) lim 0 x x f x → g x = D: f () () x gx > 2.下列结论不正确的是( ) A: sin lim 1 x x →∞ x = B: ( ) 1 lim sin ln =1 x x → C: 1 0 lim(1 ) x x x e → + = D: () 0 sin ( ) ( ) lim 0 x x ϕ x ϕ → ϕ = 3. 函数 cos ( ) x f x e = 不是( ) A:偶函数 B:单调函数 C:有界函数 D:周期函数 4.设函数 f ( ) x 在[,] a b 上连续,则下列结论错误的是( ) A: f ( ) x 在[,] a b 上有界 B: f ( ) x 在[,] a b 上必有最大值和最小值 C:若 fafb () () 0 < ,则至多有一点ξ ( ) a b < < ξ ,使 f () 0 ξ = D:若 f () () a C fb < < ,则至少有一点ξ ( ) a b < < ξ ,使 f ( ) ξ = C

南阳师范学院一数学与统计学院 5.下列结论错误的是() A:x=0是fm)=sn的第一类间断点 五m42tt2 6F- B队点“受是=m:的无穷间斯点 1斜 & cl是o- ,的可去间断点 五.证明题(共14分) D:x=0是/-过的跳跃间断点 1.证明函数y-任=到在x=1处极限不存在.(8分) x-1 三。填空题(将正确答案填写在空格上,每小题2分,共12分) 2.证明方程x3+x-1=0至少有一个根介于0与1之间.(6分) 1若00 在定义域内连续。 3.ing(arcsinx+arccosx)= a+x xs0. 5岩 6m+行= 四.计算题(每小题4分,共2分) 上 2名台 3.m1+2x) 4回[rm] 第2页共2页
南阳师范学院—数学与统计学院 第 2 页 共 2 页 5. 下列结论错误的是( ) A: x = 0 是 1 f x( ) sin x = 的第一类间断点 B:点 2 x π = 是 f ( ) tan x x = 的无穷间断点 C: x =1是 2 1 ( ) 1 x f x x − = − 的可去间断点 D: x = 0 是 ( ) x f x x = 的跳跃间断点. 三.填空题(将正确答案填写在空格上,每小题 2 分,共 12 分) 1. 若 22 0 n x n = ⎨⎪ + ≤ ⎩ 在定义域内连续
南阳师范学院一数学与统计学院 《高等数学》第一章—函数与极限 二.单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码填在题干上 的括号内。每小题2分,共10分) 自测题(B) 1.若mf)=0,mg)-1,则下列结论不一定正确的是() 题号 一 三 六 总分 得分 A:im(gf)=0(c≠0) B:lim[f(x)+g(x)= 一判断题(判断下列各题是否正确,正确的划,错误的划×.每小题2分,共24分) 6一碧0 D:f(x)>g(x) 1数列分+-是发散数列 () 2.下列结论正确的是() 2.若im.=im则数列收敛 () 3.m)=)ef)=j3)+a,(其中ma=0) () B:lim(cosin(x-1))=1 4无限个无穷小量之积仍为无穷小量 () C:lim(l-x)i=e 马二-0 5.由于y=xCosx在(0,+o)内为无界量,所以该函数在(0,+o)内一定 3.函数f)=e不是() 是无穷大量 () A:偶函数 B:有界函数 6若四=4则了0 () C:单调函数 D:周期函数 7.函数y=立图形的水平渐近线为x=1. () 4.设函数f(x)在[a,)上连续,则下列结论错误的是() 8.若a~d,B~f,则必有2a+5B~2'+5f () A:f产(x)在(a,b)上必有最大值和最小值 9.当x→0时,e2-1是比x高阶的无穷小量 () B:f(x)+1在(a,b)上有界 10.y=3 arctanx在(←A,+o)上是单调递增的. () C:若f(af(b)<0·则至少有一点5(a<5<b),使f(5)=0 山.函数f)=子simx是x→时的无穷小量 () D:若fa<C<f⑥),则至少有一点5a<5<b),使f产(=C () 第1页共2页
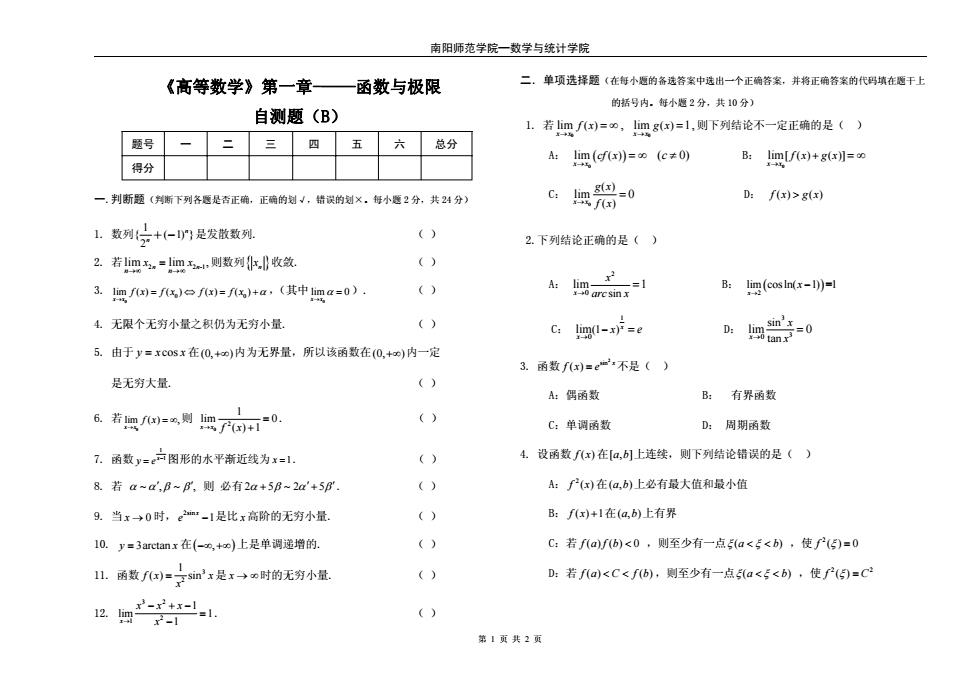
南阳师范学院—数学与统计学院 第 1 页 共 2 页 《高等数学》第一章-——函数与极限 自测题(B) 题号 一 二 三 四 五 六 总分 得分 一.判断题(判断下列各题是否正确,正确的划√,错误的划×。每小题 2 分,共 24 分) 1. 数列 1 { ( 1) } 2 n n + − 是发散数列. ( ) 2. 若 2 2 -1 lim lim , n n n n x x →∞ →∞ = 则数列{ xn }收敛. ( ) 3. 0 0 0 lim ( ) ( ) ( ) ( ) x x fx fx fx fx α → = ⇔= + ,(其中 0 lim 0 x x α → = ). ( ) 4. 无限个无穷小量之积仍为无穷小量. ( ) 5. 由于 yx x = cos 在(0, ) +∞ 内为无界量,所以该函数在(0, ) +∞ 内一定 是无穷大量. ( ) 6. 若 0 lim ( ) , x x f x → = ∞ 则 0 2 1 lim 0 x x → f x() 1 = + . () 7. 函数 1 x 1 y e − = 图形的水平渐近线为 x =1. () 8. 若 α ∼ ∼ αβ β ′ ′ , , 则 必有25 2 5 α + βα β ∼ ′ + ′ . () 9. 当 x → 0 时, 2sin 1 x e − 是比 x 高阶的无穷小量. ( ) 10. y x = 3arctan 在( ) −∞ +∞ , 上是单调递增的. ( ) 11. 函数 3 21 f ( ) sin x x x = 是 x → ∞时的无穷小量. ( ) 12. 3 2 2 1 1 lim 1 x 1 xxx → x − +− = − . () 二.单项选择题(在每小题的备选答案中选出一个正确答案,并将正确答案的代码填在题干上 的括号内。每小题 2 分,共 10 分) 1. 若 0 lim , ( ) x x f x → = ∞ 0 lim 1, ( ) x x g x → = 则下列结论不一定正确的是( ) A: ( ) 0 lim ( 0) ( ) x x cf x c → = ∞ ≠ B: 0 lim[ ( ) ( )] x x f x gx → + = ∞ C: 0 ( ) ( ) lim 0 x x g x → f x = D: f () () x gx > 2.下列结论正确的是( ) A: 2 0 sin lim 1 x x → arc x = B: ( ) 2 lim cosln( 1) =1 x x → − C: 1 0 lim(1 ) x x x e → − = D: 3 3 0 sin tan lim 0 x x → x = 3. 函数 2 sin ( ) x f x e = 不是( ) A:偶函数 B: 有界函数 C:单调函数 D: 周期函数 4. 设函数 f ( ) x 在[,] a b 上连续,则下列结论错误的是( ) A: 2 f ( ) x 在(,) a b 上必有最大值和最小值 B: f x() 1+ 在(,) a b 上有界 C:若 fafb () () 0 < ,则至少有一点ξ ( ) a b < < ξ ,使 2 f () 0 ξ = D:若 f () () a C fb < < ,则至少有一点ξ ( ) a b < < ξ ,使 2 2 f ( ) ξ = C