
第五节函数的极值与最大值最小值
第五节 函数的极值与最大值最小值

一、函数的极值及其求法 1. 极值的定义 设函数y=fx)的定义域为D.如果存在x,的某一邻域U(x)cD,使得对任意 的xeU(x), (1)都有fw)≤fx)则称函数y=f在点x,处有极大值fx,.点x,称为极大值点 (2)都有f(x)≥fx), 则称函数y=fx)在点,处有极小值fx).点x,称为极小值点 极大值和极小值统称为极值;极大值点和极小值点统称为极值点
一、函数的极值及其求法 设函数y f x ( )的定义域为D .如果存在 0 x 的某一邻域 0 U x D ( ) ,使得对任意 的 0 x U x ( ), 1. 极值的定义 (1)都有 0 f x f x ( ) ( ) 则称函数y f x ( )在点 0 x 处有极大值 0 f x( ).点 0 x 称为极大值点. (2)都有 0 f x f x ( ) ( ) ,则称函数y f x ( )在点 0 x 处有极小值 0 f x( ) .点 0 x 称为极小值点. 极大值和极小值统称为极值;极大值点和极小值点统称为极值点

一、函数的极值及其求法 2 极值的判定 定理1(必要条件)设函数∫(x)在x点处可导,且在xo点取得极值,则必有 f'(x)=0 注记1:可导函数的极值点一定是驻点.但驻点却不一定是极值点. 如y=x的驻点是x=0,但函数在在x=0附近无极值 注记2:函数的极值点可能是驻点也可能是不可导的点.如函数 f(x)=x在点x=0处不可导,但函数在x=0处取到极小值
定理 1 (必要条件) 设函数 f (x)在 0 x 点处可导,且在 0 x 点取得极值,则必有. 2 极值的判定 0 f x ( )=0 注记 1:可导函数的极值点一定是驻点. 但驻点却不一定是极值点. 如 3 y x 的驻点是 x 0,但函数在在x 0附近无极值 一、函数的极值及其求法 注记 2:函数的极值点可能是驻点也可能是不可导的点. 如函数 f (x) x 在 点 x 0处不可导,但函数在 x 0处取到极小值
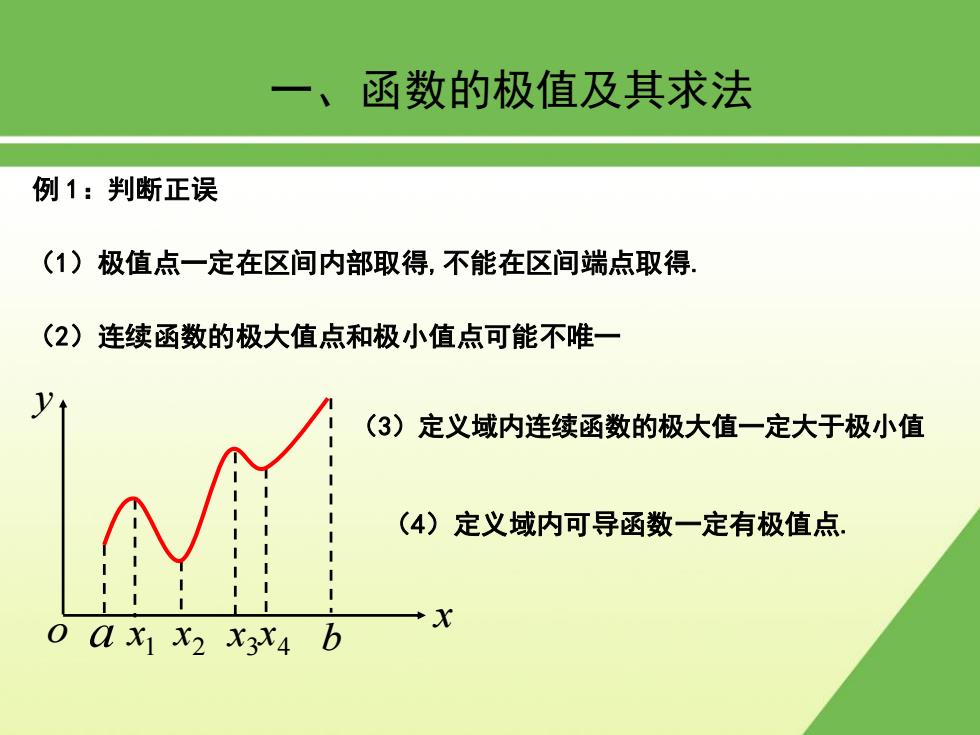
一、函数的极值及其求法 例1:判断正误 (1)极值点一定在区间内部取得,不能在区间端点取得。 (2)连续函数的极大值点和极小值点可能不唯一 (3)定义域内连续函数的极大值一定大于极小值 (4)定义域内可导函数一定有极值点. X o ax x2 x3X4 b
1 x 4 x3 x 2 a x b x o y 例 1:判断正误 (1)极值点一定在区间内部取得,不能在区间端点取得. (2)连续函数的极大值 点和极小值点可能不唯一 (3)定义域内连续函数的极大值一定大于极小值 (4)定义域内可导函数一定有极值点. 一、函数的极值及其求法

一、函数的极值及其求法 问题1:如何判断函数的驻点是函数的极值点?, 问题2:如何判断函数的不可导点是极值点?
问 题 1 :如何判断函数的驻点是函数的极值点?, 问题 2:如何判断函数的不可导点是极值点? 一、函数的极值及其求法

一、 函数的极值及其求法 定理2(第一充分条件) 设fx)在x,处连续,且在x,的某去心邻域U(,6)内可导 (1)若x∈(x。-d,)时, fx)>0 而x∈(,x。+d)时, fx)0 则 f(x)在点x处取得极小值 (3):若x∈U(x,⊙)时,f"x)的符号保持不变,则f)在x,处没有极值
定理 2 (第一充分条件) 设 f (x)在 0 x 处连续,且在 0 x 的某去心邻域 ( , ) x0 内可导. (1) 若 ( , ) 0 0 x x x 时, f (x) 0, 而 ( , ) x x0 x0 时, f (x) 0, 则 f (x)在点 0 x 处取得极大值; f (x)在点 0 x 处取得极小值. 一、函数的极值及其求法 (2) 若 ( , ) 0 0 x x x 时, f (x) 0, 而 ( , ) x x0 x0 时, f (x) 0, 则 (3):若 ( , ) x x0 时, f (x)的符号保持不变,则 f (x)在 0 x 处没有极值

一、函数的极值及其求法 注记3:如果函数fx)在所讨论的区间内连续,除个别点外处处可导,那 么就可以按下列步骤来求f()在该区间内的极值点和极值: 第一步:确定函数fx)的定义域; 第二步:求函数的导数f'(x),并求出fx)的所有驻点及不可导点; 第三步:列表判定函数的导数∫'(x)在每一个驻点和不可导点左右两侧的符号 第四步:利用第一充分条件得到极值点和相应的极值
注记 3:如果函数 f (x)在所讨论的区间内连续,除个别点外处处可导,那 么就可以按下列步骤来求 f (x) 在该区间内的极值点和极值: 第一步: 确定函数 f (x)的定义域; 第二步:求函数的导数 f (x),并求出 f (x)的所有驻点及不可导点; 第三步:列表判定函数的导数 f (x)在每一个驻点和不可导点左右两侧的符号 第四步:利用第一充分条件得到极值点和相应的极值. 一、函数的极值及其求法
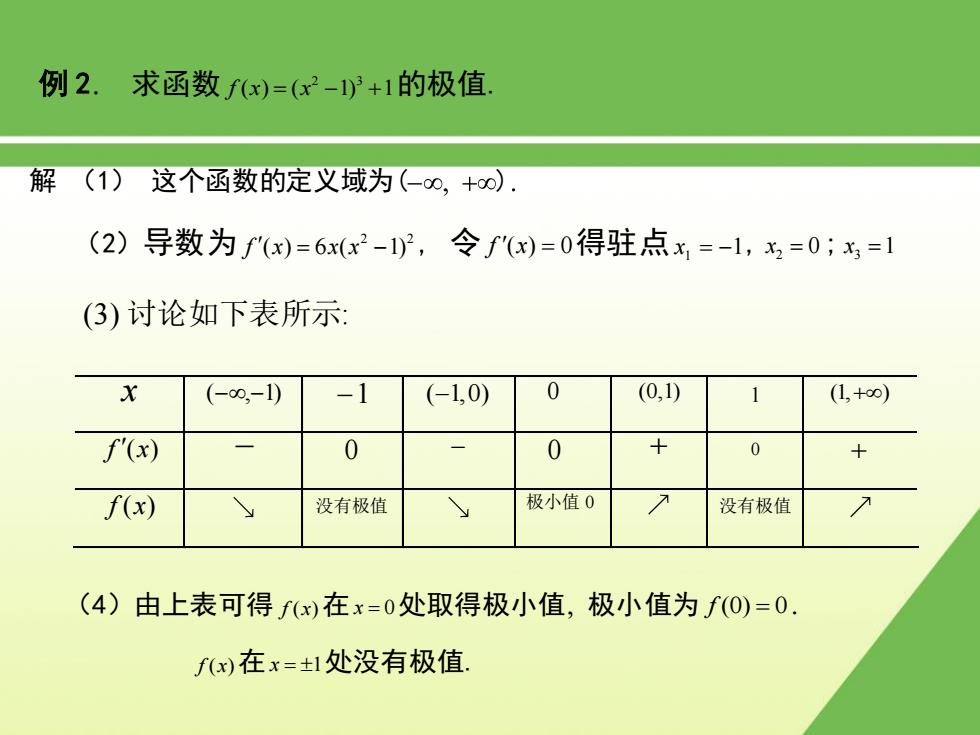
例2.求函数fx)=6x2-1)+1的极值 解 (1)这个函数的定义域为(-0,+0). (2)导数为f()=6xx2-1,令f"()=0得驻点x,=-1,=0;x=1 (3)讨论如下表所示: (-0,-1) (-1,0) 0 (0,1) (1,+o∞) f'(x) 0 0 0 f(x) 没有极值 极小值0 没有极值 (4)由上表可得fx在x=0处取得极小值,极小值为f0)=0. f)在x=士1处没有极值
(2)导数为 2 2 f x x x ( ) 6 ( 1) , 令 f (x) 0得驻点x1 1, 2 x 0 ; 3 x 1 解 (1) 这个函数的定义域为( ) 例 2 求函数 2 3 f x x ( ) ( 1) 1 的极值. x (,1) 1 ( 1,0) 0 (0,1) 1 (1, ) f x ( ) 0 - 0 0 f (x) 没有极值 极小值 0 没有极值 (3) 讨论如下表所示: (4)由上表可得 f x( )在x 0处取得极小值 极小值为 f (0) 0 f x( )在x 1处没有极值

例3求函数fx)=1-(x-2)的极值. 解:(1)函数的定义域为(-0,+0). (2) 当x≠2时,)= 2 3x-2 x=2为函数的不可导点 (3)讨论如下表所示: (-00,2) 2 (2,+∞) f'(x) 不存在 f(x) 极大值1 (4)由上表可得函数f(x)在x=2处取得极大值f(2)=1
例 3 求函数 2 3 f x x ( ) 1 ( 2) 的极值. 解 (1)函数的定义域为( ) (2) 当x 2时, 3 2 ( ) 3 2 f x x x 2为函数的不可导点 x ( ,2) 2 (2,+ ) f (x) + 不存在 - f (x) 极大值 1 (4) 由上表可得函数 f (x)在 x 2处取得极大值 f (2) 1 (3) 讨论如下表所示:

问题 如果f在驻点x,处的二阶导数f"x)存在,那么可否用 二阶导数的符号来判定x是极值点?
问题 如果 f x( )在驻点 0 x 处的二阶导数 0 f x ( )存在,那么可否用 二阶导数的符号来判定 0 x 是极值点?