§7.2点的坐标与向量的坐标 主要 内容 空间直角 向量运算 坐标系 的坐标 表示 向量在轴 上的射影
主 要 内 容 向量在轴 上的射影 空间直角 坐标系 向量运算 的坐标 表示 §7.2 点的坐标与向量的坐标
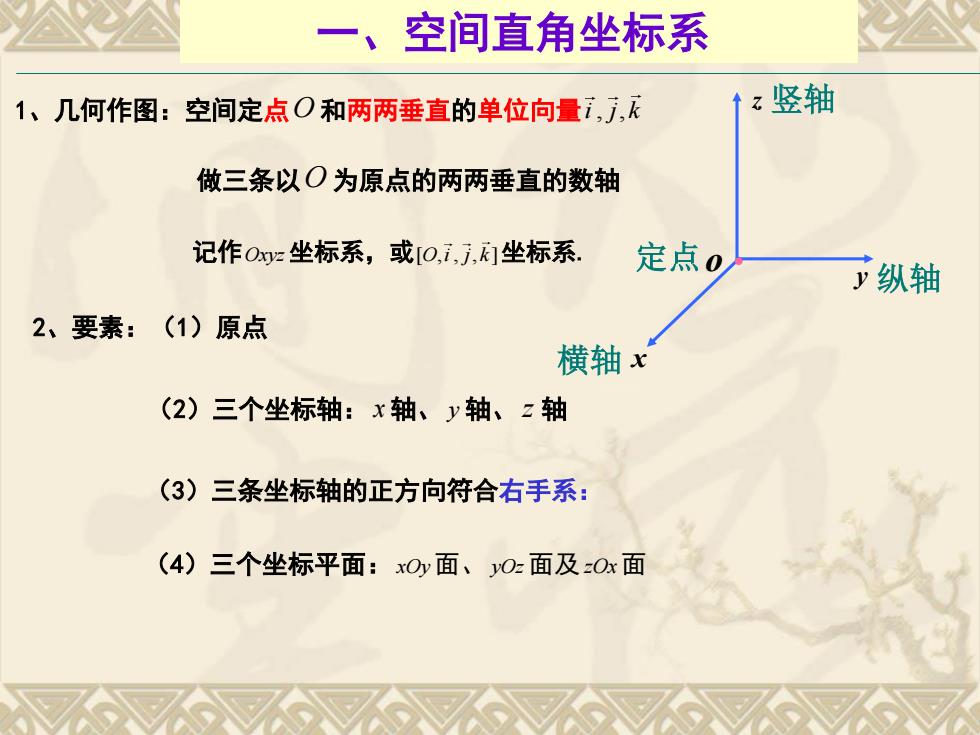
一、空间直角坐标系 1、几何作图:空间定点O和两两垂直的单位向量i,, z竖轴 做三条以O为原点的两两垂直的数轴 记作0z坐标系,或[O,i,j,们坐标系 定点0 立纵轴 2、要素: (1)原点 横轴x (2)三个坐标轴:x轴、y轴、z轴 (3)三条坐标轴的正方向符合右手系: (4)三个坐标平面:xOy面、O:面及0x面
横轴 x y 纵轴 z 竖轴 定点 o 一、空间直角坐标系 1、几何作图:空间定点 O 和两两垂直的单位向量 i j k , , 做三条以O 为原点的两两垂直的数轴 记作 Oxyz 坐标系,或 [ , , , ] O i j k 坐标系. 2、要素:(1)原点 (2)三个坐标轴: x 轴、 y 轴、 z 轴 (3)三条坐标轴的正方向符合右手系: (4)三个坐标平面:xOy 面、 yOz 面及 zOx 面

一、空间直角坐标系 (3)三个坐标面将空间共分八个卦限 z0x面 J0z面 IV- x0y面 VI
Ⅶ x o y z xoy 面 yoz 面 zox 面 (3) 三个坐标面将空间共分八个卦限 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅷ 一、空间直角坐标系
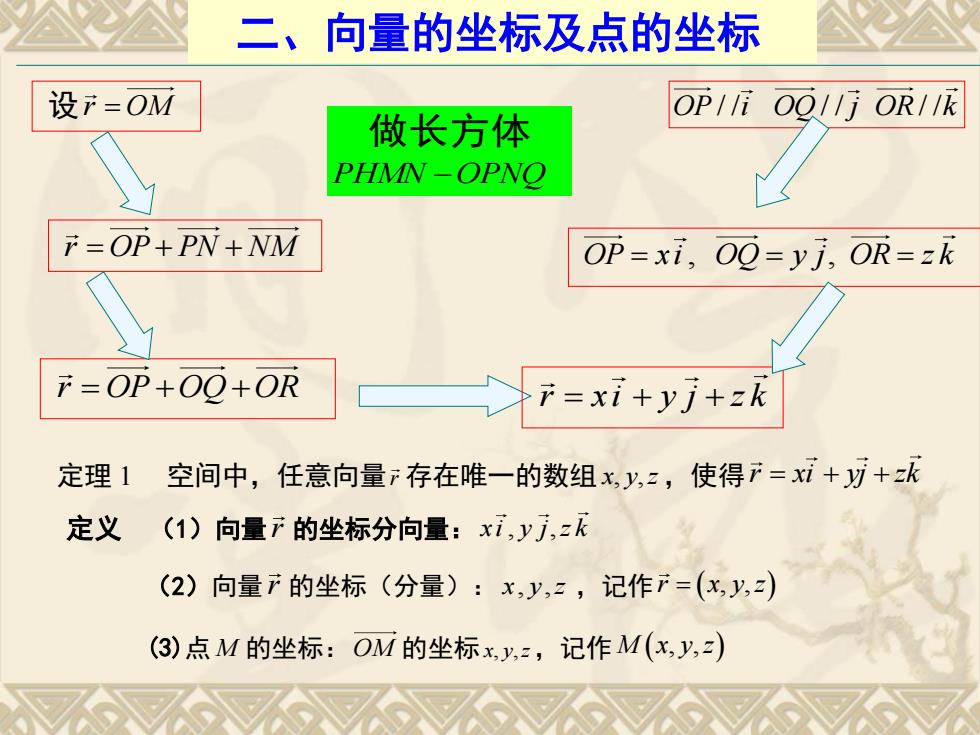
二、向量的坐标及点的坐标 设F=OM OPI/00ll OR/Ik 做长方体 PHMN-OPNO =OP+PN+NM OP=xi,00=yj,OR=zk =OP+00+OR F=xi+yj+zk 定理1 空间中,任意向量F存在唯一的数组x,y,2,使得产=xi++k 定义 (1)向量产的坐标分向量:xi,y,z (2)向量产的坐标(分量):x,y,z,记作产=(xy,) (3)点M的坐标:OM的坐标x,y,z,记作M(x,y,2)
二、向量的坐标及点的坐标 设r OM 做长方体 PHMN OPNQ r OP PN NM r OP OQ OR OP i OQ j OR k / / / / / / OP xi OQ y j OR z k , , r xi y j z k 定理 1 空间中,任意向量 r 存在唯一的数组 x, y,z,使得r xi yj zk 定义 (1)向量 r 的坐标分向量: xi y j z k , , (2)向量 r 的坐标(分量): x y z , , ,记作 r x y z , , (3)点 M 的坐标: OM 的坐标x y z , , ,记作 M x y z , ,

三、利用坐标作向量的线性运算 定理2:设a=(a,a,a),6=(6,b,),元为实数,则 (D)a+b=(as+bs;a,+b,a:+b) (2)元d=(2a,元ay,元a) (3)b/1a,(a≠0)→b:a.=b,:a,=b:a 定理3:设P(a,b,C),D(a2,b2,c2)则PP2=(a-a,b2-b,C2-c) 定理4:设M,(x1,y1,1)和M2(x2,2,2),若MM=1MM,则 oM=+o+0)-(经+2 1+
三、利用坐标作向量的线性运算 定理 2:设 ( , , ), ( , , ), x y z x y z a a a a b b b b 为实数,则 1 ( , , ) x x y y z z ()a b a b a b a b (2) ( , , ) x y z a a a a (3) ,( 0) : : : b a a b a b a b a x x y y z z 定理 3:设 1 1 1 1 2 2 2 2 P a b c P a b c ( , , ), ( , , ) 则 1 2 1 2 1 2 1 2 PP a a b b c c ( , , ) 定理 4:设 ( , , ) 1 1 1 1 M x y z 和 ( , , ) 2 2 2 2 M x y z ,若 M1M MM2 ,则 1 2 1 2 1 2 1 2 1 , , 1 1 1 1 x x y y z z OM OM OM

四、向量在轴上的投影 投影 设点M与一轴u,通过M作垂直于轴u的平面Ⅱ,称 该平面与轴u的交点M'叫做点M在轴u上的投影点: 设Od=2e,则数入称为向量在u轴上的投影 (或分量),记作Prj,OM或(OM
设点 M 与一轴u ,通过M 作垂直于轴u 的平面 ,称 M O e M u 该平面与轴u 的交点M 叫做点M 在轴u 上的投影点. 设OM e , 则数 称为向量 r 在u 轴上的投影 (或分量),记作Pr u j OM 或( ) OM u 投影 四、向量在轴上的投影

四、向量在轴上的投影 定理5:(1) Prj,a=alcoso其中p为d与u轴夹角 (2) Prj(@+b)=Prj@+Prjb (3) Pr j(Aa)=APr ja 注记:(1) Prj,a=|acos∠(a,b),b≠0 (2) Prja(a+b)=Prjga+Prjb c+0 (3) Prj6(a)=Prj,ab≠0
四、向量在轴上的投影 定理 5:(1) Pr cos u j a a 其中 为 a 与u 轴夹角 (2) Pr ( ) Pr Pr u u u j a b j a j b (3) Pr ( ) Pr u u j a j a 注记:(1) Pr cos ( , ), 0 b j a a a b b (2) Pr ( ) Pr Pr 0 c c c j a b j a j b c (3) Pr ( ) Pr 0 b b j a j a b

四、 例题 例1:m=3i+5j+8k,方=2i-4j-7, 例2:若a=-2i+3j+nk与 p=5i+j-4k,a=5m+3n-p b=mi-6j+2X平行,求m,n 解:由向量坐标的定义可得 解:由向量坐标的定义可得 m=(3,5,8),n=(2,-4,-7) a=(-2,3,n) p=(5,1,-4) 6=(m,6,2) 向量线性运算的坐标的表达式可得 由于两向量共线,故对应坐标成比例 à=5(3,5,8)+3(2,-4,-7)-(5,1,-4) -2:3:n=m:(-6):2 =(16,12,23)=16i+12j+23k, 因此 m=4,n=-1
四、 例 题 例 1: m i j k n i j k 3 5 8 , 2 4 7 , p i j k 5 4 , 求 a m n p 5 3 例 2:若 a i j nk 2 3 与 b mi j k 6 2 平行,求m n, 解:由向量坐标的定义可得 m n 3,5,8 , 2, 4, 7 p 5,1, 4 向量线性运算的坐标的表达式可得 a 5 3,5,8 3 2, 4, 7 5,1, 4 16,12,23 16 12 23 , i j k 解:由向量坐标的定义可得 a n 2,3, b m , 6,2 由于两向量共线,故对应坐标成比例 2:3: :( 6) : 2 n m 因此 m n 4, 1