
第二节 最小二乘拟合多项式 一、最佳平方逼近问题 二、最小二乘拟合多项式
一、最佳平方逼近问题 二、最小二乘拟合多项式 第二节 最小二乘拟合多项式

一、最佳平方逼近问题 最佳平方逼近问题的提法是:设()是[a,]上的连续函数, H是所有次数不超过n的多项式的集合,在H,中求()逼近 f(),使-L-p(s[/-)=V-P 此时称()为f(x)在[a,]上的最佳平方逼近多项式。 我们将要研究P()是否存在?是否唯一?如何求得()
最佳平方逼近问题的提法是:设 是 上的连续函数, 是所有次数不超过 的多项式的集合,在 中求 逼近 ,使 此时称 为 在 上的最佳平方逼近多项式。 我们将要研究 是否存在?是否唯一?如何求得? a b, n H n P x n ( ) f x( ) ( ( ) ( ) ( ) ) ( ) 1/ 2 2 2 2 inf n b n n a P x H f P x f x P x dx f P − = − = − H n f x( ) P x n ( ) P x n ( ) a b, f x( ) P x n ( ) 一、最佳平方逼近问题
二、最小二乘拟合多项式 例1 测得铜导线在温度X时的电阻y如下 温度x 19.1 25.0 30.1 36.0 40.0 45.1 50.0 电阻y 76.30 77.80 79.25 80.80 82.35 83.9085.10 求电阻少和温度X间的关系
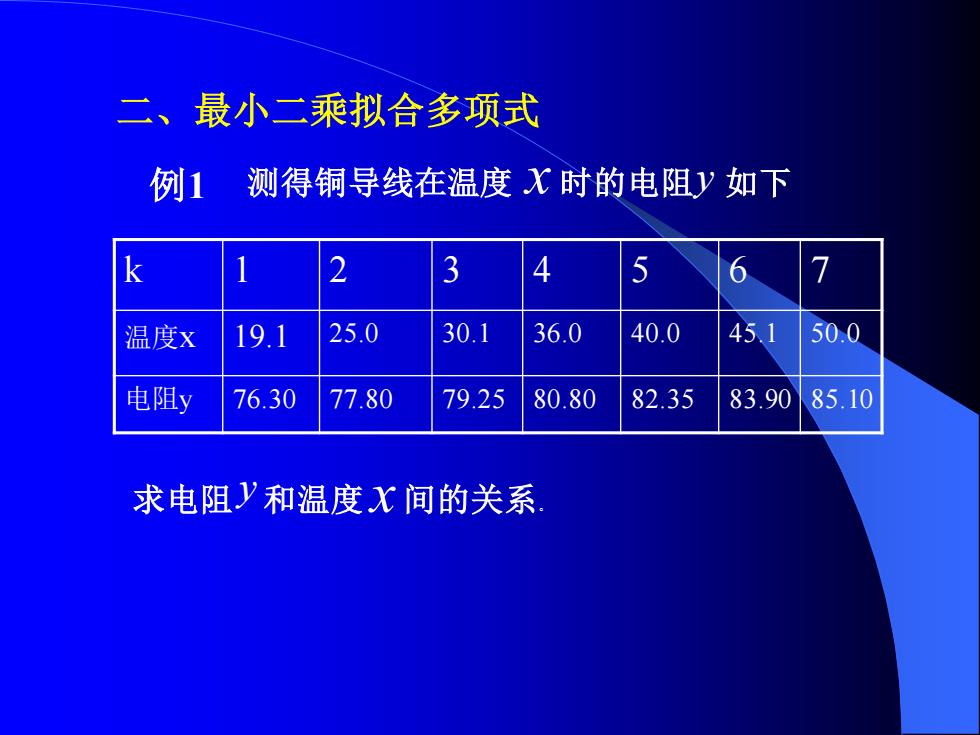
二、最小二乘拟合多项式 例1 求电阻 和温度 x 间的关系。 y 测得铜导线在温度 x 时的电阻 y 如下 k 1 2 3 4 5 6 7 温度x 19.1 25.0 30.1 36.0 40.0 45.1 50.0 电阻y 76.30 77.80 79.25 80.80 82.35 83.90 85.10

解决这类问题通常的步骤如下: (1)用一坐标将X,y值描于图上 (2)凭视觉翹,y)在一条直线 上的两测附近,于是可没X,近 似的成直线关。≈少=ax十b 上面的直线关系称为数学模型。在第飞次观测数据中,少与 实测值y有误差 k=yx-=y-(a+bx),k=1.2,...,n Ek通常称为残差
解决这类问题通常的步骤如下: x y (1)用一坐标将 x , y 值描于图上 (1) (2)凭视觉知, 在一条直线 上的两测附近,于是可设 , 近 似的成直线关系。 ( , ) i i x y y x y y ax b = + ˆ 上面的直线关系称为数学模型。在第 次观测数据中, 与 实测值 有误差 k y ˆ k y k k k k k = − = − + = y y y a bx k n ˆ ( ), 1, 2, , 2.1 ( ) k 通常称为残差

它是衡量被确定的参数Q和b(也就是近似多项式 )=a+bx)好坏的重要标志。 确定参数A,b原则: ①使残差绝对值中最大的一个达到最小,即T=maxs为最小 ②使残差绝对值之和达到最小,即∑为最小 ③使残差的平方和达到最小,即∑为最小; 。原则③确定待定参数,从而得到近似多项式的方法,就是 通常所说的最小二乘法
它是衡量被确定的参数 和 (也就是近似多项式 )好坏的重要标志。 a b y a bx ˆ = + 确定参数 a , b 原则:, ①使残差绝对值中最大的一个达到最小,即 为最小; ②使残差绝对值之和达到最小,即 为最小; ③使残差的平方和达到最小,即 为最小; max k k T = k k 2 k k ① 原则③确定待定参数,从而得到近似多项式的方法,就是 通常所说的最小二乘法

用最小二乘法确定参数☑和b,应使 8(a,)-(.-a+ 取最小值。因此,应有 2∑(0-(a+x)0 2∑(x-(a+bx)水=0 由此,得到如下线性方程组 空+空- 解之有a=70.527,b=0.291从而得近似多项式 y=70.572+0291x
用最小二乘法确定参数 a 和 b ,应使 ( ) ( ( )) 7 2 1 , k k k a b y a bx = = − + 取最小值。因此,应有 ( ( )) 7 1 2 0 k k k y a bx = − + = ( ( )) 7 1 2 0 k k k k y a bx x = − + = 由此,得到如下线性方程组 7 7 1 1 7 2 7 2 1 1 1 7 k k k k k k k k k k k a b x y a x b x x y = = = = = + = + = 解之有 a b = = 70.527, 0.291 y x ˆ = + 70.572 0.291 从而得近似多项式

一般来说,设给定一组数据 (x,y),k=1,2.,m (2.2) 则适当选择系数a,a,…a.(n<m)后,使 δ(a,4a)=∑(4-P.(》 (2.3) 达到最小的多项式 Pn(x)=anx”+.tax+ao 2.4 称为数据(2.2)的最小二乘拟合多项式,或变量x,y之间的 数学模型(经验公式)
一般来说,设给定一组数据 ( x y k m k k , , 1, 2 , 2.2 ) = ( ) 则适当选择系数 a a a n m 0 1 , , n ( ) 后,使 ( ) ( ( )) ( ) 2 0 1 1 , , 2.3 m n k n k k a a a y P x = = − 达到最小的多项式 ( ) 1 0 (2.4) n P x a x a x a n n = + + + 称为数据 的最小二乘拟合多项式,或变量 之间的 数学模型(经验公式)。 (2.2) x y

由于8排负,且为a,4,a。的二次多项式,故δ(4o,41,,an) 必有最小值,其最小值可如下求得: 令: a6=0,U=0,lm Da; 即 2-4-ag-a=0 (0=0,1,2n) 或写成 (j=0,1,…,n 引进记号 则上述方程组成为
即 或写成 ( 0 1 ) ( ) 1 0, 0,1, 2, m n j k k n k k k y a a x a x x j n = − − − = = ( ) 1 0 1 1 1 1 1 , 0,1, , m m m m j j j j n k k k k n k k k k k y x a x a x a x j n + + = = = = = + + + = 由于 非负,且为 的二次多项式,故 必有最小值,其最小值可如下求得: 0 1 , , n a a a (a a a 0 1 , , , n ) 0, 0,1, ( ) j j n a = = 令: 引进记号 则上述方程组成为 1 1 m m j j j k j k k k k s x u y x = = = =

S4+S+4+…+S+nan=4J=0,1,,n) (2.5) 这是P(x)系数ao,41,,an满足的方程组,称为正规方程 组(或法方程组)。 可以证明,当x0,X1,…,x互异时,该方程组有唯一解 ao,41,…,4n它们使得(23)取最小值。如此,我们便得 到了最小二乘拟合多项式P(x)
s a s a s a u j n j j j n n j 0 1 1 + + + = = + + , 0,1, , 2.5 ( ) ( ) 这是 系数 满足的方程组,称为正规方程 组(或法方程组)。 P x n ( ) 0 1 , , , n a a a 可以证明,当 x x x 0 1 , , , n 互异时,该方程组有唯一解 0 1 , , , n a a a 它们使得 (2.3) 取最小值。如此,我们便得 到了最小二乘拟合多项式 P x n ( )

例7 设已知函数f(x)的表列值为 X 0.2 0.5 0.7 0.85 1.221 1.649 2.014 2.3402.718 试按最小二乘法构造f(x)的二次近似多项式。 解 经简单计算可得关于参数4,4,4的方程组为 5a+3.250a1+2.503a2=9.942, 3.250a+2.503a,+2.090a2=70185 2.503a+2.090a+1.826a2=5.857 解之得a=1.036,a=0.751,a2=0.928,故 B(x)=1.036+0.751x+0.928x2
例7 设已知函数 f x( ) 的表列值为 试按最小二乘法构造 f x( ) 的二次近似多项式。 0.2 0.5 0.7 0.85 1 1.221 1.649 2.014 2.340 2.718 y x 解 经简单计算可得关于参数 a a a 0 1 2 , , 的方程组为 0 1 2 0 1 2 0 1 2 5 3.250 2.503 9.942, 3.250 2.503 2.090 70185, 2.503 2.090 1.826 5.857. a a a a a a a a a + + = + + = + + = 解之得 a a a 0 1 2 = = = 1.036, 0.751, 0.928, 故 ( ) 2 2 P x x x = + + 1.036 0.751 0.928