
§5.二次型及其标准型 在解析几何中,为了便于研究二次曲线 ● ax"+bxy+cy2 =1 。的几何性质,我们可以选择适当的坐标变换: x=x'cose-y'sin 0 y x'sin 0+y'cos0 把方程化为标准形 mx2+ny'2=1
§5. 二次型及其标准型 ⚫ 在解析几何中,为了便于研究二次曲线 ⚫ ⚫ 的几何性质,我们可以选择适当的坐标变换: ⚫ ⚫ 把方程化为标准形 1 (1) 2 2 ax +bxy+ cy = = + = − sin cos cos sin y x y x x y 1 2 2 mx + ny =

ax2+bxy+cy2 =1 (1) (1)的左边是一个二次齐次多项式,从代数学的观点看, 化标准型的过程就是通过变量的线性变换化简一个二次齐 次多项式,使它只有平方项。这样的问题,在许多理论问 题或是实际问题中常会遇到。 现在我们把这类问题一般化,讨论个变量的二次齐 次多项式的化简问题
(1)的左边是一个二次齐次多项式,从代数学的观点看, 化标准型的过程就是通过变量的线性变换化简一个二次齐 次多项式,使它只有平方项。这样的问题,在许多理论问 题或是实际问题中常会遇到。 现在我们把这类问题一般化,讨论n个变量的二次齐 次多项式的化简问题。 1 (1) 2 2 ax +bxy+ cy =

一、」 二次型概念 定义1:含有n个变量x1,x2,…xn的二次齐次函数 f(x)=ax+2a2x2+2axx +a22X2+…+2a2nX2x =∑∑ax 其中 a ji 2arxxj =arx xj+anxxi
一、二次型概念 定义1:含有n个变量x1 , x2 ,…xn的二次齐次函数 n n n f x x x a x a x x a x x 1 2 1 2 1 1 2 1 2 1 1 1 ( , , , ) = + 2 ++ 2 n n a x a x x 2 2 2 22 2 + ++ 2 2 nn n ++ a x = = = n i n j ij i j a x x 1 1 i j j i i j i j i j i j j i j i a = a , 2a x x = a x x + a x x 其中

二次型的矩阵形式 fx…,x)=∑∑a, i=1= =x (ax +a2x2+...+ainx,) +x2(a21x1+a22x2+…+a2mxn) +xn (anx+an2x2++amxn)
二次型的矩阵形式 = = = n i n j n i j i j f x x x a x x 1 1 1 2 ( , ,, ) 1 11 1 12 2 1 2 21 1 22 2 2 1 1 2 2 ( ) ( ) ( ) = + + + + + + + + + + + + + n n n n n n n nn n x a x a x a x x a x a x a x x a x a x a x

ax1+a2X2+…+anxn =(X1,x2,…,Xn) a21+022+…ta2mxn anlX1+an2X2+…+amxn =(x…xn〉 21 02 02n an nn Xn x"Ax
+ + + + + + + + + = n n n n n n n n n n a x a x a x a x a x a x a x a x a x x x x 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 ( , , , ) ( ) 11 12 1 1 21 22 2 2 1 2 1 2 n n n n n nn n a a a x a a a x x x x a a a x = T = x Ax

其中 多多 1)称A为二次型f的矩阵,显然A=AT: 2)A=(a以,若a,为复数,称f为复二次型: 3)A=(a/,若a为实数,称f为实二次型: 4)称为(A)为二次型f的秩
其中 = = n n n n n n n x x x x a a a a a a a a a A 2 1 1 2 2 1 2 2 2 1 1 1 2 1 , 1)称A为二次型 f 的矩阵,显然 A=AT; 2)A=(aij), 若 aij 为复数,称 f 为复二次型; 3) A=(aij), 若 aij 为实数,称 f 为实二次型; 4)称为R(A)为二次型 f 的秩

例1.把下面的二次型写成矩阵形式: f(x,x)=x+4x2+3x (2 f(x1,x2,x3)=x2+4xx2+3x 解:0=63 2 (②)0,3)=632 3 x
例 1. 把下面的二次型写成矩阵形式; (1) ( , ) 4 3 ; 2 1 2 2 2 1 2 1 f x x = x + x x + x (2) ( , , ) 4 3 ; 2 1 2 2 2 1 2 3 1 f x x x = x + x x + x ( ) = 3 2 1 1 2 3 1 2 3 0 0 0 2 3 0 1 2 0 (2) ( , , ) x x x f x x x x x x ( ) 1 1 2 1 2 2 1 2 1 2 3 x f x x x x x = 解:( ) ( , )
二、二次型的标准形 定义9.称只含有平方项的二次型 f=y+3y+…+2ny =(y…y) y"Ay 为二次型的标准型(或法式)
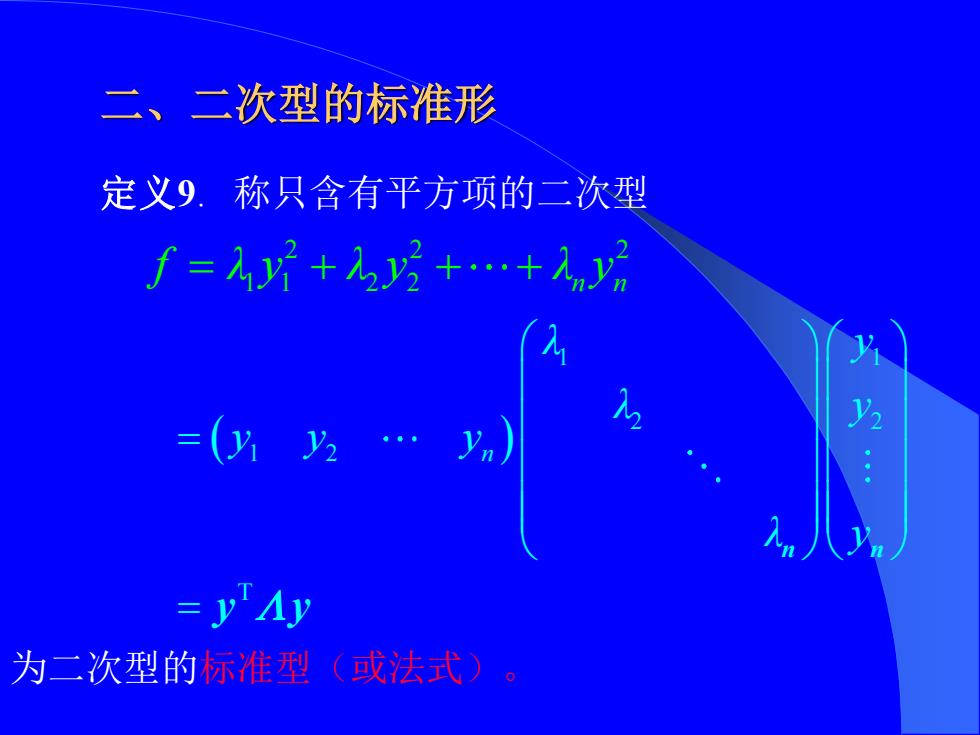
二、二次型的标准形 定义9. 称只含有平方项的二次型 为二次型的标准型(或法式)。 2 2 2 = + + + 1 1 2 2 n n f λ y λ y λ y ( ) 1 1 2 2 1 2 T n n y y = = n λ y λ y y y y λ y

所谓一般二次型的化简问题,就是寻找一个可逆的线 性变换: x Cy+C22++Cinyn X2=C21y1+C222++C2nym Xn=Cny+Cn22+Cmyn 即 x=cy 把f=xAx化成标准型。于是 f=xAx=(cy)'A(cy)=y(c'Ac)y
所谓一般二次型的化简问题,就是寻找一个可逆的线 性变换: T T T T f x Ax cy A cy y c Ac y = = = ( ) ( ) ( ) . T 即 把 化成标准型。于是 x cy f x Ax = = 1 11 1 12 2 1 2 21 1 22 2 2 1 1 2 2 = + + + = + + + = n n n n n n n nn n x c y c y c y x c y c y c y x c y +c y + +c y

定理9任给可逆矩阵C,令B=CTAC,若A为对称 矩阵,则B亦为对称矩阵,且R(B)=R(A)。 证:A为对称矩阵,即有AT=A,子是, BT=CTAC)T=CTAT(C )T=CTAC=B. 故B为对称矩阵 再证R(B)=R(A) 因 B=CTAC故R(B)≤R(AC)R(A) 又因A=(C)BC1,故R(A)≤R(BC-I)≤R(B) 于是 R(B)=R(A)
定理9 任给可逆矩阵 C ,令 B=C TAC,若 A 为对称 矩阵,则 B 亦为对称矩阵,且 R(B)=R(A)。 证: A为对称矩阵,即有 A T=A,于是, B T =(C TAC) T=C TAT(C T) T=C TAC=B . 故 B 为对称矩阵. 再证 R(B)=R(A). 因 B=C TAC, 故 R(B) ≤R(AC) ≤R(A). 又因 A=(C T) -1BC -1 ,故 R(A) ≤R(BC -1 ) ≤R(B) 于是 R(B)=R(A)