
五、线性相关性基本定理 定理2向量组a1,a2,…,am(m之2)线性相关的充 分必要条件是向量组中至少有一个向量可由其余的-1个 向量线性表示。 证充分性,不妨设am可由其余的向量线性表示,即有 am=九1a1+2a2+…+九m-1am-l 从而 入1a1+22++1m-1am-1+(l)am=0 因为21,2,,m-,-1这m个数不全为零,故a1,a2, am线性相关
五、线性相关性基本定理 定理2 向量组 α1,α2,… ,αm ( m ≥ 2 )线性相关的充 分必要条件是向量组中至少有一个向量可由其余的 m-1个 向量线性表示。 证 充分性,不妨设αm可由其余的向量线性表示,即有 αm= λ1α1 + λ2α2 + … + λm-1αm-1 从而 λ1α1 + λ2α2 + … + λm-1αm-1 + (-1)αm = 0 因为 λ1,λ2,… ,λm-1 , -1 这 m 个数不全为零,故α1,α2,…, αm 线性相关

必要性设a1,a2,, am线性相关,即有不全为0 的数k1,2,…,飞nm使 k a+k2z++kmcm= 不妨设k夫0,从而有 k k 即a,能由其余的m-1个向量线性表示
必要性 设α1,α2,…,αm线性相关,即有不全为 0 的数 k1 , k2 , … , km 使 k1α1 + k2α2 + … + kmαm = 0 不妨设 k1 ≠ 0,从而有 2 3 1 2 3 1 1 1 m m k k k k k k = − − − − 即 α1能由其余的 m-1个向量线性表示

例2设a7=(a1,a2,an),e1T=(1,0,…,0)月 2T=(0,1,…,0),…,emI=(0,0,,1),讨论向量组的线性 相关性。 解显然 aT=ae taze2"++anen 由定理2知,向量组a,eT,e2T,…,enT线性相关
例2 设 α T = ( a1 , a2 , … , an ) , e1 T = ( 1, 0, … , 0 ), e2 T = ( 0, 1, … ,0 ),… ,en T= ( 0, 0, …, 1) , 讨论向量组的线性 相关性。 解 显然 由定理2知,向量组 α T , e1 T , e2 T , … , en T 线性相关。 α T = a1 e1 T +a2 e2 T + … + an en T

定理3设a1,a2,,am线性无关,而a1,a2,, am,阝线性相关,则阝能由a1,a2,·,am线性表示, 且表示式是唯一的。 证因a1,a2,,am阝线性相关,故有k1,,kmkm+1 不全为0,使 ka++kmam+kmB= 要证印能由a1,a2,…,am线性表示,知须证明km*1≠0 用反证法,假设km+1=0,则k1,2,,飞m不全为0,且有 k an k2a2 ++kmam=0 这与a1,a2,,am线性无关矛盾,此矛盾说明km≠0 从而有 B=- k m
定理3 设 α1 , α2 , … , αm 线性无关,而 α1,α2,…, αm,β 线性相关,则 β 能由 α1,α2,… ,αm 线性表示, 且表示式是唯一的。 证 因 α1,α2,…,αm,β 线性相关,故有k1 ,…,km,km+1 不全为 0 ,使 k1α1 + … + kmαm + km+1β = 0 要证β 能由 α1 , α2 , … , αm 线性表示,知须证明 km+1 ≠ 0 。 用反证法,假设 km+1= 0 , 则 k1 , k2 , … , km不全为 0 ,且有 k1α1 + k2α2 + … + kmαm= 0 这与 α1,α2,…,αm 线性无关矛盾,此矛盾说明 km+1 ≠ 0 。 从而有 1 2 1 2 1 1 1 m m m m m k k k k k k + + + = − − − −

再证表示式的唯一性。设有两个表示式 阝=八1a1+2a2++m0m 阝=k1a1+k2a2++km0m 两式相减,得 (1-k)a1+(2-)a2++(2nm-km)am=0 因a1,a2,,anm线性无关,所以2,-k=0即 2=k(i=1,2,,m)。 故表示式是唯一的
再证表示式的唯一性。设有两个表示式 β =λ1 α1 + λ2α2 + … + λmαm β = k1α1 + k2α2 + … + kmαm 两式相减,得 (λ1-k1 )α1 +(λ2-k2 )α2 + … + (λm-km)αm = 0 因 α1 ,α2 ,…,αm 线性无关,所以 λi-ki = 0 即 λi = ki ( i = 1, 2, … , m ) 。 故表示式是唯一的

作业127页1、2、 128贤5
作业 127 页 1 、 2 、 128 页 5

§3线性相关性的判定 一、方程组矩阵←→向量组的关系 ax +a2x2 +...+amnx,b a2X1+a2X2+…+41mXm=b mX+am23+…+amXn=b a A 2 0 'm2 mn
§3 线性相关性的判定 一、方程组↔矩阵↔向量组的关系 11 1 12 2 1 1 21 1 22 2 1 2 1 1 2 2 n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b + + + = + + + = + + + = (1) 11 12 1 1 1 21 22 2 2 2 1 2 n n m m mn n m a a a x b a a a x b a a a x b =

即 Ax三b 将A按列分块,由(2)得 X1C1+X2a2+…+xn0n=b (3 显然,由(3)式知,若b能由a,a2,,an线性表 示, 则线性方程组(1)有解,若b不能由a1,a2,·,a 线性表示,则线性方程组(1)无解: 当b=0时,(3)式变为x1a1+x302++x6n=0(4) 显然,由(4)知,若a1,a2,,an线性相关,则它所 对应的齐次线性方程组Ax=0有非零解,若a1,a2,·,am 线性无关,则Ax=0仅有零解。 综上所述,向量b能不能由向量组a1,a2,,an线性表 示,则说明它所对应的非齐次的线性方程组Ax=b有没有 解的问题;向量组a1,a2,…,an的线性相关性,则说明它所 对应的齐次线性方程组Ax=0有什么样的解的问题
即 Ax = b (2) x1α1 + x2α2 + … + xnαn = b (3) 显然,由(3)式知,若 b 能由α1 , α2 , … , αn 线性表 示,则线性方程组(1)有解,若 b 不能由 α1 , α2 , … , αn 线性表示,则线性方程组(1)无解; 当 b = 0时,(3)式变为 x1α1 + x2α2 + … + xnαn = 0(4) 显然,由(4)知,若 α1 , α2 , … , αn 线性相关,则它所 对应的齐次线性方程组 Ax = 0 有非零解,若 α1 , α2 , … , αn 线性无关,则 Ax = 0 仅有零解。 综上所述,向量b能不能由向量组 α1 , α2 , … , αn 线性表 示,则说明它所对应的非齐次的线性方程组 Ax = b 有没有 解的问题;向量组α1 , α2 , … , αn的线性相关性,则说明它所 对应的齐次线性方程组 Ax = 0 有什么样的解的问题。 将A按列分块,由(2)得
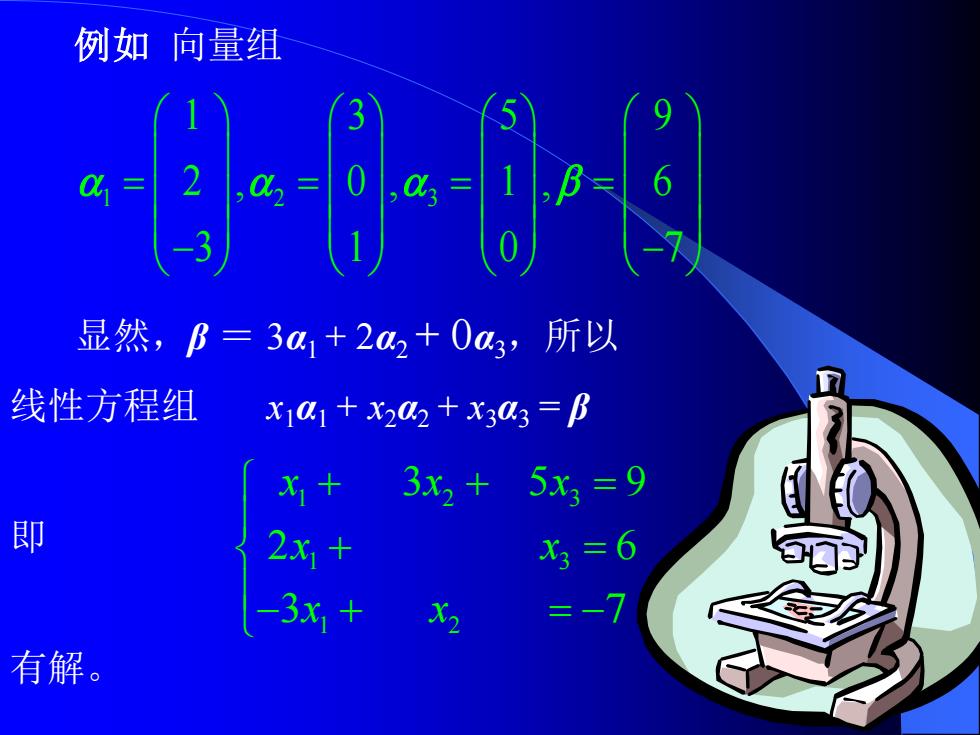
例如向量组 a 6 显然,B=3a1+2a2+0a3,所以 线性方程组 x1a1+x202+x3a3 B x+3x2+5x3=9 即 2x1+ x3=6 -3x+x =-1 有解
例如 向量组 显然,β = 3α1 + 2α2 + 0α3,所以 线性方程组 x1α1 + x2α2 + x3α3 = β 即 1 2 3 1 3 1 2 3 5 9 2 6 3 7 x x x x x x x + + = + = − + = − 有解。 1 2 3 1 3 5 9 2 , 0 , 1 , 6 3 1 0 7 = = = = − −

向量组 得 由于a1,a2,B线性无关,所以B不能由a1,a线性表 示, 即线性方程组x1a1+x2a2=阝 x+ 3x2 =1 亦即 一x1+ X2 无解
向量组 由于 α1,α2,β 线性无关,所以β 不能由α1,α2线性表 示,即线性方程组 x1α1 + x2α2 = β 亦即 1 2 1 1 2 3 1 1 0 x x x x x + = = − + = 无解。 1 2 1 3 1 1 , 0 , 1 1 1 0 = = = −