
注意:亦可利用矩阵的初等 列变换求解逆矩阵 事实上:因为 A=(D2…D) =…P 〔r-e- 所以 列变换
注意:亦可利用矩阵的初等 列变换求解逆矩阵. 事实上:因为 1 1 2 1 ( ) − − A = PP Pl 1 1 1 2 −1 − − = Pl P P = = − − − − 1 1 1 1 A E EA AA A E A ~ −1 A E E A 列变换 所以

2、利用矩阵的初等行变求 解矩阵方程 事实上,对于AX=B 若A可逆,则有 X-AAX-AB 对应于: A'(AB)=(EAΓB 即 (MB)(44'B)
2、利用矩阵的初等行变求 解矩阵方程. ⚫ 事实上,对于 AX = B 若A可逆,则有 X A AX A B −1 −1 = = 对应于: A (A B) (E A B) −1 −1 = 即 ( ) ( ) 1 A B A A B 行变换 ~ −

例3.设AX=B,求X,其中 2 71 A= 2 B 3 3 43 解若A可逆,则X=AB 12325 (4B)= 22 0-2-5-1-9 34343 0-2-6-2-12
例3. 设 AX = B , 求 X . 其中 解 若 A 可逆,则 X A B −1 = ( ) = 3 4 3 4 3 2 2 1 3 1 1 2 3 2 5 A B − − − − − − − − 0 2 6 2 12 0 2 5 1 9 1 2 3 2 5 ~ 1 2 3 2 5 2 2 1 , 3 1 3 4 3 4 3 A B = =

12325)10-21-4 0-2-5-1-90-2-5-1-9 0-2-6-2-1200-11-3 2 710 0 0 6 01 -3 011300 所以 2 3
− − − − − − − − 0 2 6 2 12 0 2 5 1 9 1 2 3 2 5 ~ − − − − − − − − − 0 0 1 1 3 0 2 5 1 9 1 0 2 1 4 ~ − 0 0 1 1 3 0 2 0 4 6 1 0 0 3 2 ~ − − 0 0 1 1 3 0 1 0 2 3 1 0 0 3 2 ~ 所以 = − − 3 3 2 1 2 3 X

同理亦可求解矩阵方程 YA=C 若A可逆,则有 Y=CA 即 e.acajl
同理亦可求解矩阵方程 YA =C 若 A 可逆,则有 −1 Y = CA 即 ~ −1 CA E C A 列变换
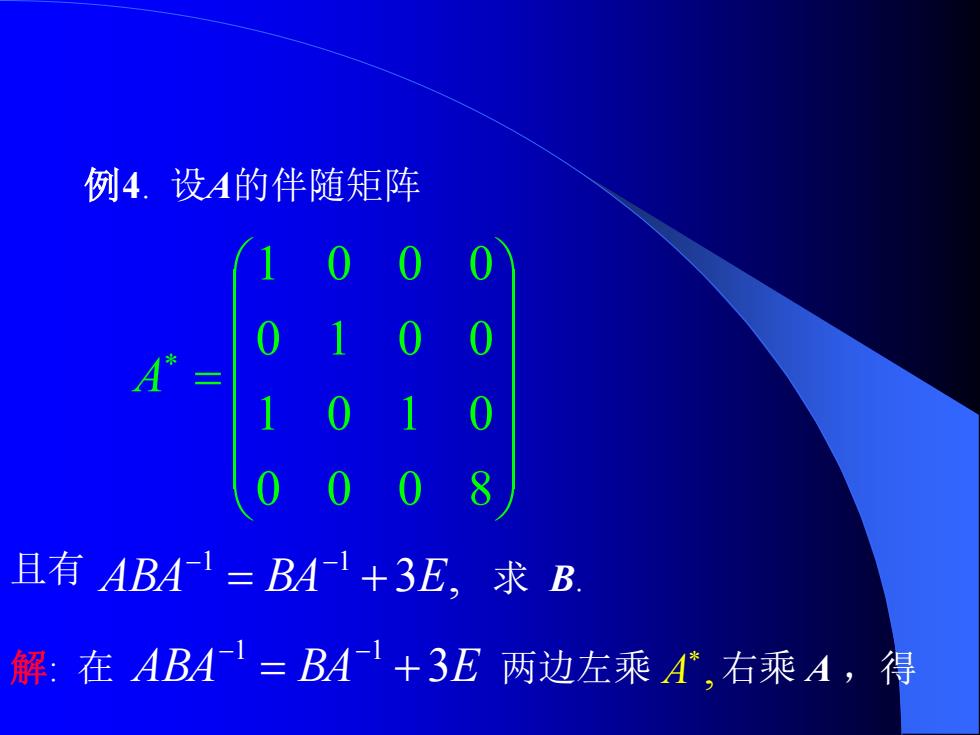
例4.设A的伴随矩阵 00 且有ABA1=BA1+3E,求B 解:在ABA=BA+3E两边左乘A,右乘A,得
例4. 设A的伴随矩阵 = 0 0 0 8 1 0 1 0 0 1 0 0 1 0 0 0 A 且有 3 , 1 1 ABA = BA + E − − 求 B. 解: 在 ABA BA 3E 1 1 = + − − 两边左乘 , A 右乘 A ,得

A(ABA)A=A(BA+3E)A 即 AABAA-ABAA+3AA (*) 因为AAAE,而A3A=8 从而有 |A=2 故(*)式可改写为2B=A*B+6E 即 (2E-A)B=6E 所以 B=6(2E-A)
A (ABA )A A (BA 3E)A 1 1 = + − − 即 因为 A A =| A| E, 而 | | | | 8, 3 = = A A 从而有 | A|= 2 (*) 故(*)式可改写为 2B = A B + 6E 即 (2E − A )B = 6E 所以 1 6(2 ) − B = E − A 1 * 1 A ABA A A BA A A A 3 − − = +

B=6(2E-A)
1 6(2 ) − B = E − A − = 0 0 0 1 6 0 6 0 0 6 0 0 6 0 0 0 1 0 0 0 0 1 0 0 6 1 0 1 0 1 000 6 = −

第三章小结 矩阵的初等换 矩阵的初等变换与线性方程组 初等方阵 矩阵的秩 线性方程组
第三章 小 结 矩 阵 的 初 等 变 换 与 线 性 方 程 组 矩 阵 的 初 等换 初 等 方 阵 矩 阵 的 秩 线 性 方 程 组

矩阵的初等变换 1.对换矩阵的两行(列) 2.用0乘矩阵的第行(列) 概念 3把某行(列)的k倍加到另一行 列)的对应元素上去 初等变换不改变矩阵的秩 性质 2:对A经过有限次初等变换得到B 则4等价B 求逆 ue)图) 用途 求矩阵A的秩、最简型、标准形
矩 阵 的 初 等 变 换 概 念 1.对换矩阵的i, j两行(列). 2.用k≠0乘矩阵的第i行(列). 3.把某i行(列)的k倍加到另一行 (列)的对应元素上去. 性 质 1.初等变换不改变矩阵的秩. 2.对A经过有限次初等变换得到B, 则A等价B. 用 途 求逆, ( ) ( ) − − 1 1 ~ ~ A E E A A E E A 列 行 求矩阵A的秩、最简型、标准形