吉林大学：《线性代数》课程教学资源（PPT课件）第二章 矩阵及其运算 11-2-1 §1.矩阵

第二章矩阵及其运算 §1矩阵 一、矩阵概念 定义1.由m×n个数a,(i=1,2,mJ=1,2,,n 排成m行n列的数表 ar 0h2 A2n Am2 a mn 称为m行n列矩阵简称m×n矩阵

第二章 矩阵及其运算 §1 矩阵 一、矩阵概念 定义1. m m mn n n a a a a a a a a a       1 2 2 1 2 2 2 1 1 1 2 1 m n a (i 1,2, ,m; j 1,2, ,n) 由  个数 i j =  =  排成m行n列的数表 称为m行n列矩阵简称, mn矩阵

为表示它是一个整体，在这数 表的两边用大圆括弧把它范围起来， 并用大写黑体字母表示： 02 021 A m2 mn

为表示它是一个整体 , 在这数 表的两边用大圆括 弧把它范围起来， 并用大写黑体字母表示:               = m m mn n n a a a a a a a a a A       1 2 2 1 2 2 2 1 1 1 2 1

例1某厂向三个商店发送四种 产品，其发送的数量和单价及单件 的重量都可用矩阵来刻划： 若用4表示为工厂向第i店发送第/种产品数量， 则矩阵 a14 A= d21 d3 d24 31 a32 33 34 表示了工厂向三个商店发送四种产品的数量

例1.某厂向三个商店发送四种 产品，其发送的数量和单价及单件 的重量都可用矩阵来刻划. 若用 表示为工厂向第 i 店发 送第 j 种产品数量， 则矩阵 aij           = 3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 a a a a a a a a a a a a A 表示了工厂向三个商店发送四种产品的数量

若用b表示第种产品的单价 b2表示第种产品单件的重量 则矩阵： B b b42 表示了这四种产品的单价及单件重量

              = 41 42 31 32 21 22 11 12 b b b b b b b b B 表示了这四种产品的单价及单件重量. , 若用bi1 表示第i种产品的单价 bi2 表示第i种产品单件的重量 则矩阵:

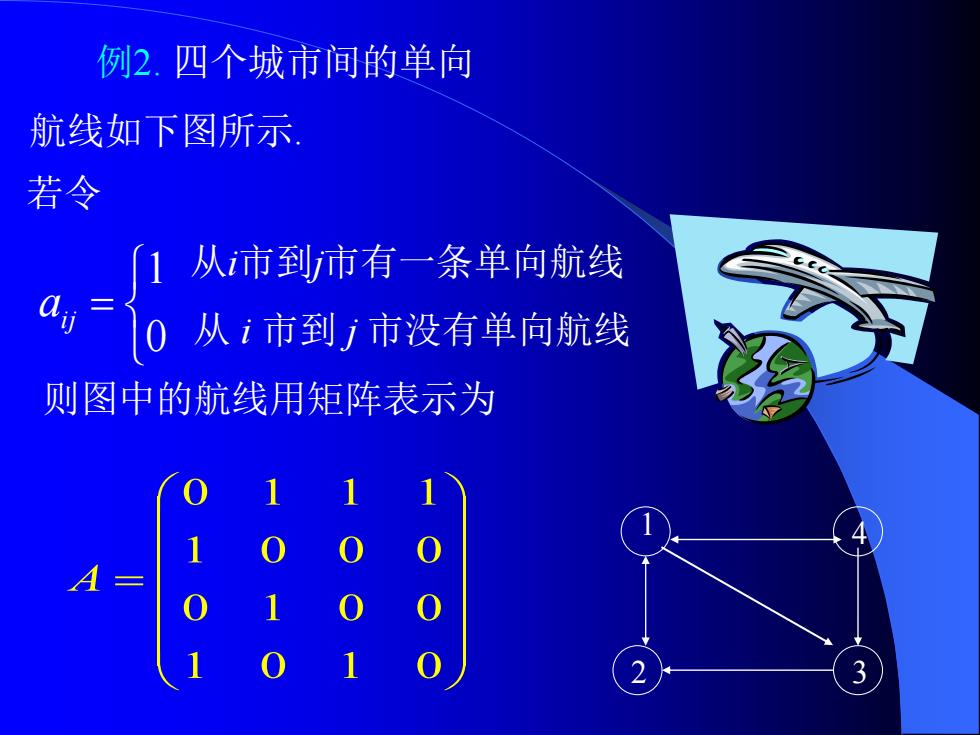
例2.四个城市间的单向 航线如下图所示 若令 1 从市到市有一条单向航线 a,=0从1市到)市没有单向航线 则图中的航线用矩阵表示为

   = 0 1 ij a               = 1 0 1 0 0 1 0 0 1 0 0 0 0 1 1 1 A 4 2 1 3 例2. 四个城市间的单向 航线如下图所示. 若令 从i市到j市有一条单向航线 从 i 市到 j 市没有单向航线 则图中的航线用矩阵表示为

例3.n个变量x1,x2,…,xn与m个变量 ,2,…,ym之间的关系式 y=a1x1 +a12x2 +..'tainxn 2=a21x1+a22X2+…+a2nxn ym amix+am2x2++amnxn 表示了一个从变量x,,…,x到变量，2，…，y的线性变换 其中a,为常数，这个线性变换的系数a,构成矩阵 2 A= ml mn

例3.               = m m mn n n a a a a a a a a a A       1 2 2 1 2 2 2 1 1 1 2 1        = + + + = + + + = + + + m m m mn n n n n n y a x a x a x y a x a x a x y a x a x a x     1 1 2 2 2 2 1 1 2 2 2 2 1 1 1 1 1 2 2 1 1 2 , , , n x x x m 个变量 与 个变量 n 1 2 , , , m y y y 之间的关系式 1 2 1 2 , , , , , , , , n m ij ij x x x y y y a a 表示了一个从变量 到变量 的线性变换 其中 为常数 这个线性变换的系数 构成矩阵

二、矩阵的表示方法 1.可用一个大写字母表示：AB,C,D,E等 2.用大写字母加上下角标表示：AB 3.A=(a或A=(a)mxn表示 三.几种特殊的矩阵 1方阵 a 02 0n1 'n2 nn

二、矩阵的表示方法 1.可用一个大写字母表示: A,B,C,D,E等 Amn Bst 2.用大写字母加上下角标表示: , 3.A = (ai j)或A = (ai j) mn 表示 三.几种特殊的矩阵 1.方阵               = n n n n n n a a a a a a a a a A       1 2 1 2 2 2 2 1 1 1 2 1

2.上三角矩阵 0 A= B= : .: 0 a n 0 3.下三角矩阵 02 B= 21 A= 02 a nn 0 02 nn

2.上三角矩阵               = nn n n a a a a a a A       0 0 0 22 2 11 12 1               = 0 0 0 1 21 22 11 12 1       n n b b b b b b B 3.下三角矩阵               = n n nn n n a a a a a B        1 2 2 1 0 0 0 0               = n n n n a a a a a a A       1 2 2 1 2 2 1 1 0 0 0

4.对角矩阵 0 5.单位矩阵 E=

4.对角矩阵                = n          0 0 0 0 0 0 2 1 5.单位矩阵               = 0 0 1 0 1 0 1 0 0        E

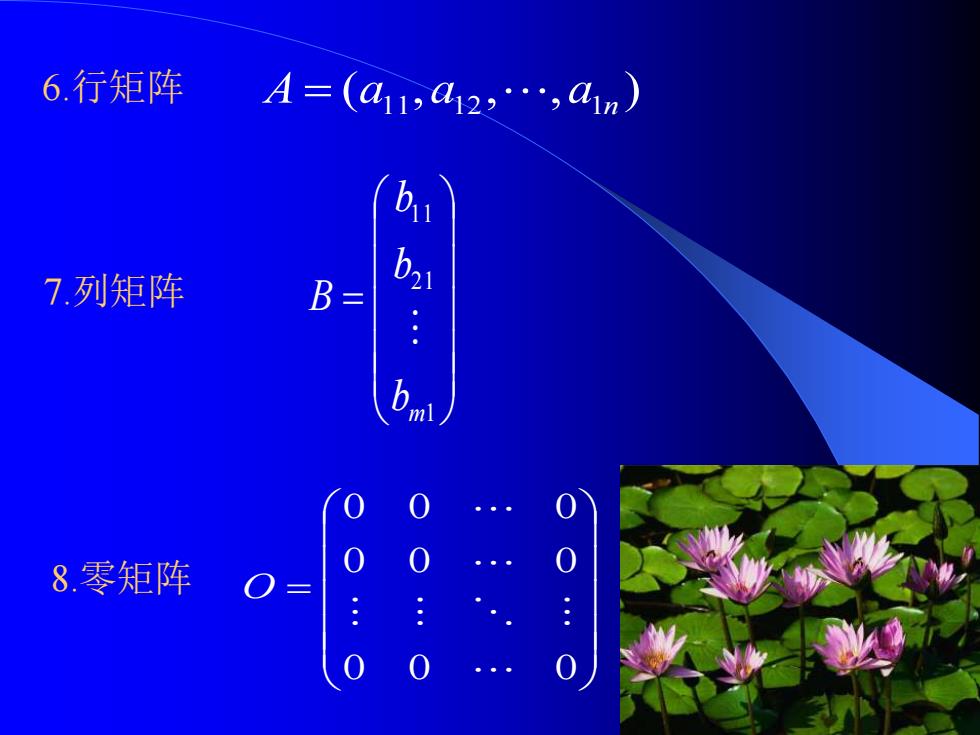
6.行矩阵 A=(a13a12,…,a1m） 7.列矩阵 B 8.零矩阵

6.行矩阵 ( , , , ) A = a11 a12  a1n 7.列矩阵               = 1 21 11 m b b b B  8.零矩阵               = 0 0 0 0 0 0 0 0 0        O