吉林大学：《线性代数》课程教学资源（PPT课件）第二章 矩阵及其运算 18-2-4 §4 分块矩阵

例1.设 A= 2 1 20 求AB

例1.设 求AB. , 1 1 0 1 1 2 1 0 0 1 0 0 1 0 0 0               − A =               − − − = 1 1 2 0 1 0 4 1 1 2 0 1 1 0 1 0 B

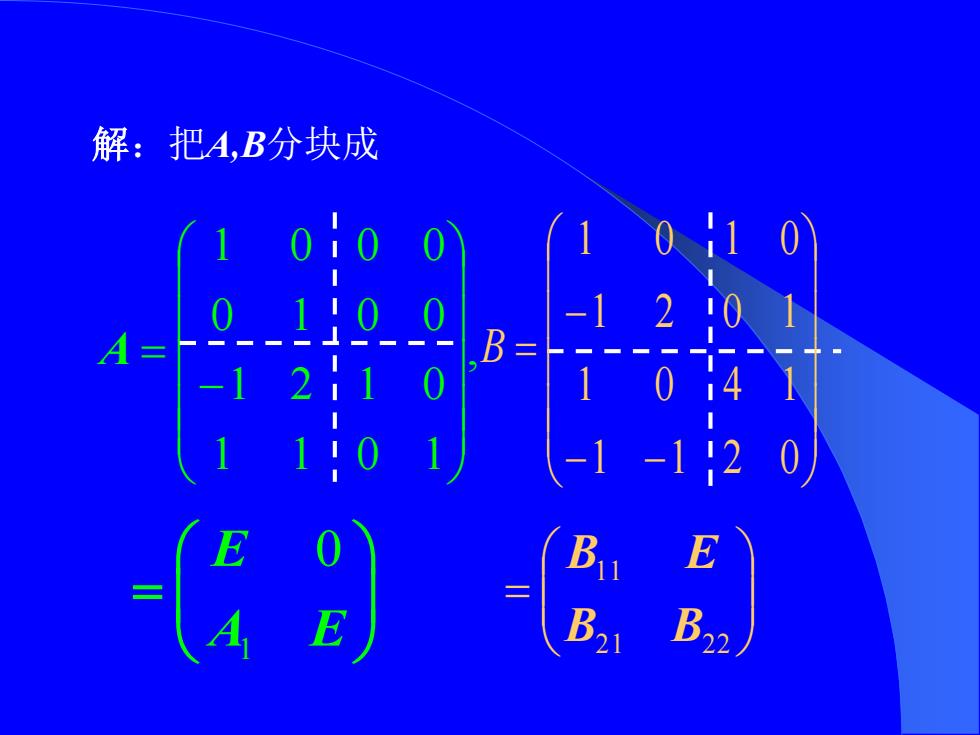
解：把A,B分块成 0 0 A= -1 2 1 B22

, 1 1 0 1 1 2 1 0 0 1 0 0 1 0 0 0               − A = 解：把A,B分块成         = 21 22 11 B B B E 1 E 0 A E  =                    − − − = 1 1 2 0 1 0 4 1 1 2 0 1 1 0 1 0 B

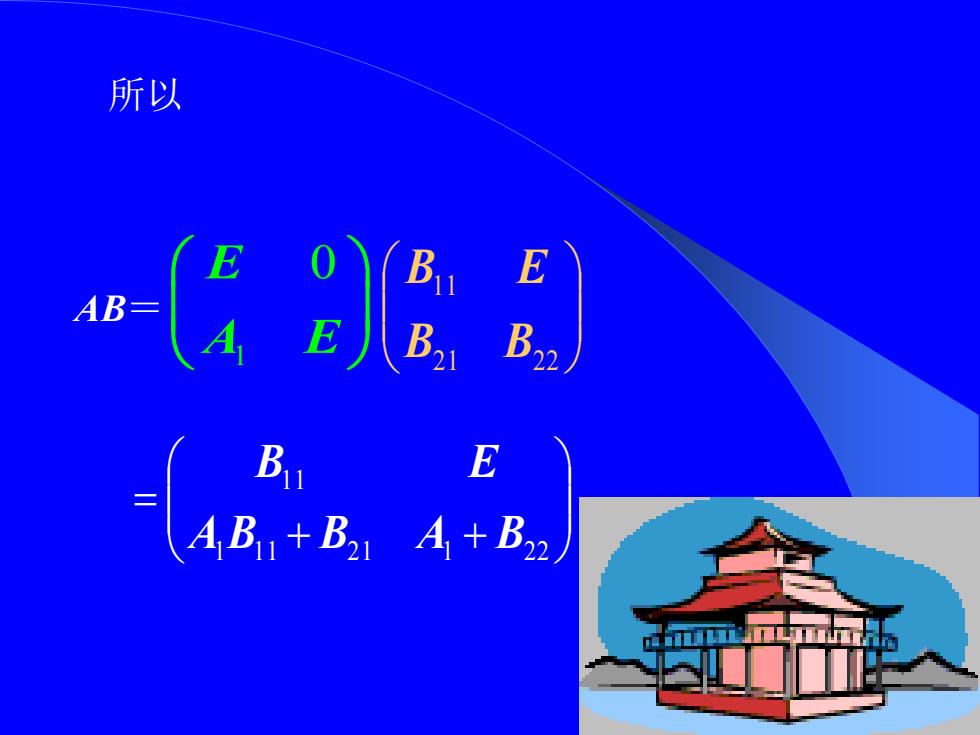
所以 (a -4ia4

所以 AB＝         21 22 11 B B B E         + + = 1 11 21 1 22 11 A B B A B B E 1 E 0 A E      

其中 4a*a-9） 4=》-台0-别 于是 AB

其中         − − +        −        − + = 1 1 1 0 1 2 1 0 1 1 1 2 A1 B1 1 B2 1 , 1 1 2 4 1 1 1 0 0 2 3 4         − − =        − − +       − =         =        +       − + = 3 1 3 3 2 0 4 1 1 1 1 2 A1 B2 2 . 1 1 3 1 2 4 3 3 1 2 0 1 1 0 1 0               − − − 于是 AB =

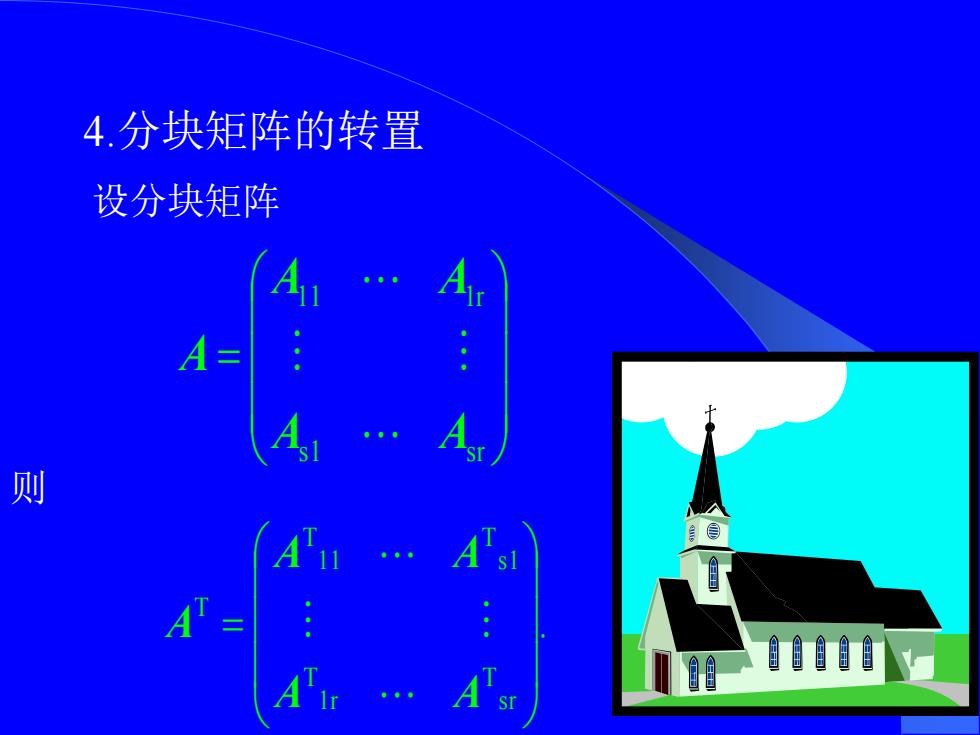
4.分块矩阵的转置 设分块矩阵 则 A"= 自自自1自

4.分块矩阵的转置 设分块矩阵           = s 1 s r 11 1r A A A A A     则 . s r T 1 r T s 1 T 1 1 T T           = A A A A A    

5.分块对角矩阵（准 对角矩阵) 设 A A= A 其中4(i=1,2,…,S)都是方子块 显然 A=444

5.分块对角矩阵（准 对角矩阵）. 设 其中               = As A A A  2 1 A (i＝1,2, ,s)都是方子块. i  . A = A1 A2  As 显然

若A,≠0(i=1,2,…,s) 则■ A≠0，所以 As

若 则 A 0 ( i 1 , 2 , , s), i  ＝  , 所以 . 1 1 2 1 1 1   = − − − − A S A A A  A  0

例2.设 解： ·群 A=⑤=g

例2. 设 1 , 0 2 1 0 3 1 5 0 0 −           A = 求A           = 0 2 1 0 3 1 5 0 0 A         = 2 1 0 0 A A 解： (5), A1 = ; 5 1 1 1       = − A

4- 4-02 3 所以 5 3

, 2 1 3 1 2         A = . 2 3 1 1 1 2         − − = − A               − = − − 0 2 3 0 1 1 0 0 5 1 1 A 所以

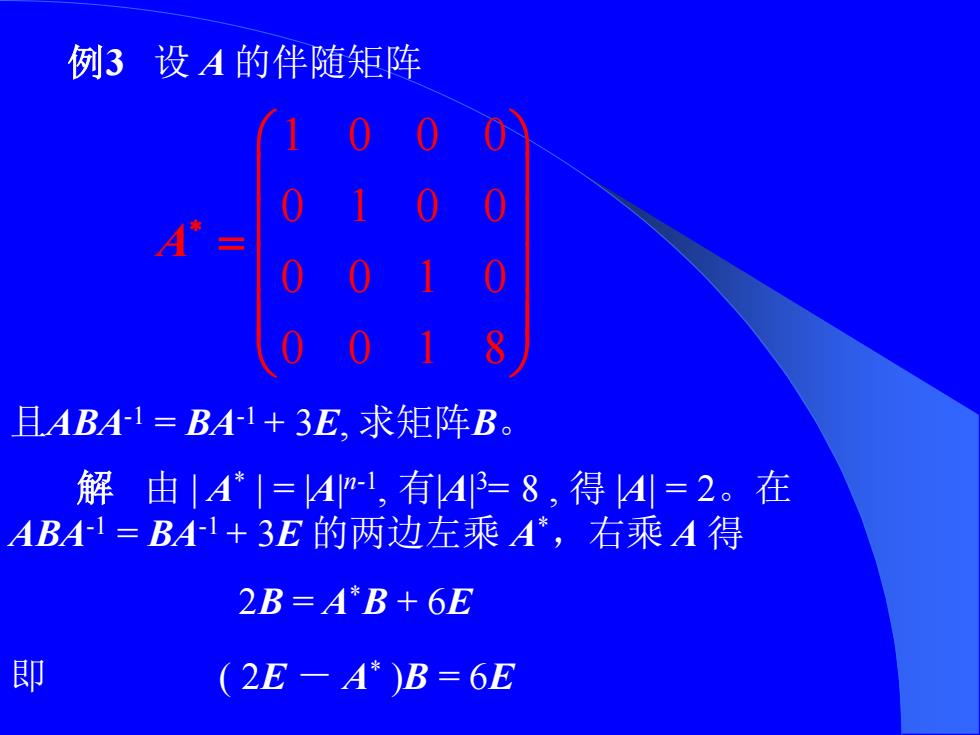
例3设A的伴随矩阵 且ABAI=BAI+3E,求矩阵B。 解由A|=4-1,有43=8，得4=2。在 ABA1=BA1+3E的两边左乘A*,右乘A得 2B=A*B+6E 即 (2E-A*)B=6E

例3 设 A 的伴随矩阵 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 8 A        =       且ABA-1 = BA-1 + 3E, 求矩阵B。 解 由 | A* | = |A| n-1 , 有|A| 3= 8 , 得 |A| = 2。在 ABA-1 = BA-1 + 3E 的两边左乘 A* ，右乘 A 得 2B = A*B + 6E 即 ( 2E － A* )B = 6E