
第一章 第四节 §4.克拉默法则 一.非齐次线性方程组的克拉默法则 设非齐次线性方程组 a1x1+a12x2+十41nxn=b a21x1+a22x2++a2nxn =b2 amx+an2x2+annxn=b
第一章 第四节 §4.克拉默法则 一.非齐次线性方程组的克拉默法则 + + + = + + + = + + + = n n n n n n n n n n a x a x a x b a x a x a x b a x a x a x b 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 (1) 设非齐次线性方程组
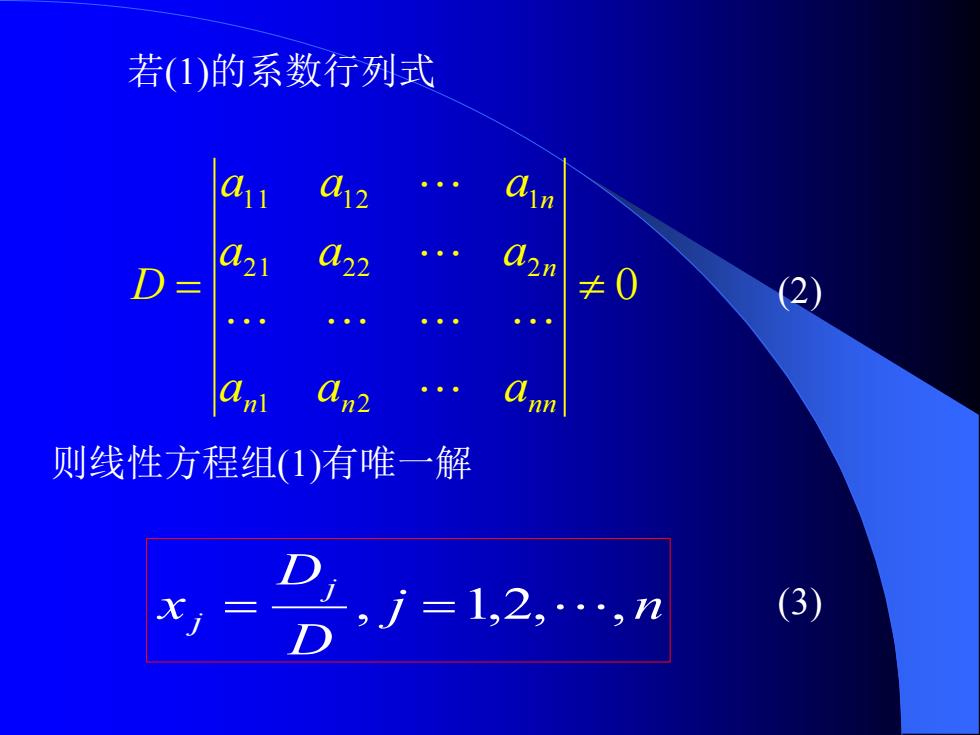
若(1)的系数行列式 a 0h2 An2 则线性方程组(1)有唯一解 x,= ,j=1,2,…,n (3)
j n D D x j j = , =1,2,, (3) 则线性方程组(1)有唯一解 若(1)的系数行列式 0 1 2 2 1 2 2 2 1 1 1 2 1 = n n n n n n a a a a a a a a a D (2)

先证x分,12n是()的解, 证明: 要球3三2“n是少的解,只须 明(3)满足(1)即可,为此把(1)改写成: ax1+a,2x2+…+amxn=b,i=1,2,…,n 即证明: a*a:a会==l2n 等式成立
j n D D x j j = , =1,2,, j n D D x j j = , =1,2,, , 1,2, , . 1 1 2 2 a x a x a x b i n i + i ++ i n n = i = , 1,2, , . 2 2 1 1 b i n D D a D D a D D a i n i + i ++ i n = = 即证明: 等式成立 证明: 先证 是(1)的解, 要证 是(1)的解,只须证 明(3)满足(1)即可,为此把(1)改写成:

做n+1阶行列式 b b b b, nn 显然Dn1=0把 Dn+t 按第一行展开.需要求出第一行 每个元素的代数余子式第一行元素C)的代数余子式为:
n n n j n n i i i j i n j n i i i j i n n b a a a b a a a b a a a b a a a D 1 1 1 1 1 1 1 1 +1 = 做n+1阶行列式 显然 . 把 按第一行展开.需要求出第一行 每个元素的代数余子式.第一行元素 的代数余子式为: Dn+1 = 0 Dn+1 aij

a.j-i a.j ,=(-1)1 an.j an.j 41 =(-1y2(-1 =(-1y2(-1yD,=-D ,j=1,2,…,n 所以 Dnt =bD-anD-aiD2--ainDn=0 即 D D2+…+anD D+an D m→b i=1,2,…,n 这说明x,= 乃J=12…n是(0的解
所以 0 Dn+1 = bi D − ai1 D1 − ai2 D2 −− ai nDn = 即 这说明 , 1,2, 是(1)的解 1,2, , 2 2 1 1 j n D D x b i n D D a D D a D D a j j i n i i i n = = + + + = = n n j n n j n n j j n j j a a b a a a a b a a 1 , 1 , 1 1 1 1, 1 1 1, 1 1 2 1 ( 1) ( 1) − + − + + − = − − ( 1) ( 1) 1,2, , . 2 1 D D j n j j = − j+ − j− = − = n n n j n j n n j j n j i j b a a a a b a a a a A 1 , 1 , 1 1 1 1 1, 1 1, 1 1 1 1 ( 1) − + − + + + = −

再证唯一性假设x,三C,j=1,2,…,力 也是(1)的解.在(2)两端同时乘以C j 0= ...ann (a191++aC,+…+4nCm) a n (amG+…+an9+…+AmnCn) n
再证唯一性.假设 也是(1)的解.在(2)两端同时乘以 x c j n j j = , =1,2, , j c n n j j n n j j n j a a c a a a c a c D 1 1 1 1 1 = n n n j j n n n n n j j n n n a a c a c a c a a a c a c a c a ( ) ( ) 1 1 1 1 1 1 1 1 1 1 1 + + + + + + + + =

nn 由于D≠0,所以 C,= 7=1,2,…,n. D 故线性方程组(1)有唯一解(3)
由于 , 所以 故线性方程组(1)有唯一解(3). D 0 j 1,2, ,n. D D c j j = = j n n n n n D a b a a b a = = 1 1 1 1 1