
三、n阶行列式的定义 定义1设有n2个数,排成n行n列的数表 a11a12…a1n 2122 ann 。作出表中位于不同行不同列的个数的 乘积,并冠以符号(-1,得到形如 (-1)airazp.anr 的项,其中PP…P为自然数1,2,…i, 的一个排列,t为这个排列的逆序数
⚫ 定义1 设有n 2个数,排成n行n列的数表 三、n阶行列式的定义 n n n n n n a a a a a a a a a 1 2 21 22 2 11 12 1 ⚫ 作出表中位于不同行不同列的n个数的 乘积,并冠以符号(-1)t,得到形如 的项,其中 为自然数1,2,…n, 的一个排列,t 为这个排列的逆序数。 1 2 1 2 ( 1) n t − a a a P P nP PP P 1 2 n

。这样的排列共有l个,所有这些项的代数 和称为n阶行列式。记为: D=入(-1)'ainazna 也可记为 D=det(ai)
⚫ 这样的排列共有n!个,所有这些项的代数 和称为n阶行列式。记为: = − P P nPn t D a a a 1 1 2 2 ( 1) det( ) D = aij ⚫ 也可记为:

行列式的其他定义 。另一种定义形式为 D=>(-1)'ag,ag22…aan 同理,也可以定义为: D=∑(-l)2+pp
行列式的其他定义 ⚫ 另一种定义形式为: + = − q p q p qn pn D a a a 1 1 2 2 ( 1) = − q q q n t n D a 1 a 2 a 1 2 ( 1) ⚫ 同理,也可以定义为:

四、几种特殊的行列式 (1)对角行列式 2 =22…人n n(n-1) (-1) 2入2…m
四、几种特殊的行列式 ⚫ (1) 对角行列式 n n 1 2 2 1 0 0 = n n n n 1 2 2 ( 1) 2 1 ( 1) 0 0 − = −
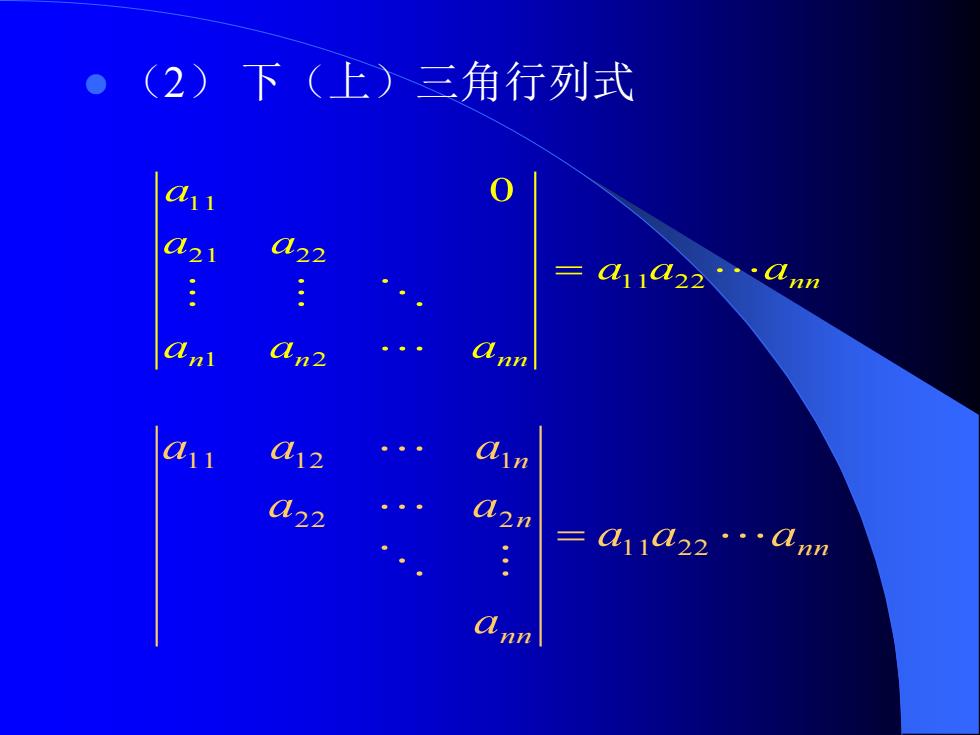
(2)下(上)三角行列式 d22 三 1122Cnn an2 ann a11 d12 。。。 d22 : q1122·ann a nn
⚫ (2) 下(上)三角行列式 n n n n n n a a a a a a a a a 1 1 2 2 1 2 2 1 2 2 1 1 0 = n n n n n n a a a a a a a a a 1 1 2 2 2 2 2 1 1 1 2 1 =

(3 d ·: .: 0 D CRI 0 .: : DD2 G C b 7n .: 0wN b 其中 b D : nn
⚫ (3) 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 D D b b b b a a a a c c b b c c b b a a a a D n n n n k kk k n n k n n n k n k kk k = = = k kk k a a a a D 1 11 1 1 = n n n n b b b b D 1 11 1 2 = ⚫ 其中

练习 。习题一 。1.(1) (3) ●2.(1) (2) (5)
练习 ⚫ 习题一 ⚫ 1. (1)(3) ⚫ 2. (1)(2)(5)

完