
第三讲 §3行列式按行(列)展开 一,余子式和代数余子式 在n阶行列式中,把元素 所在第行和第列划去后,留下 来的n一1阶行列式叫做元素 的余子式.记作M,即 4的余子式记作 0过 的躲学变-旷w
§3 行列式按行(列)展开 一.余子式和代数余子式 在n阶行列式中,把元素 所在第i行和第j列划去后,留下 来的 n- 1阶 行列式叫做元 素 的余子式.记作 .即 的余子式记作 . 的代数余子式 Mij Mij ( ) ij i j Aij M + = −1 第三讲 .... ij a ij a

例如四阶行列式 3 024 032 d33 03A 042 043 44 中元素4,的余子式和代数余子式分别为 a a13 M2=a21 d24 42=(-1)M2=-M32 an 43 04
中元素 的余子式和代数余子式分别为 4 1 4 2 4 3 4 4 3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 a a a a a a a a a a a a a a a a D = 41 43 44 21 23 24 11 13 14 32 a a a a a a a a a M = M32 a32 例如四阶行列式 ( ) 3 2 32 32 A M 1 + = − = −

二.行列式按行(列)展开定理 引理设D为n阶行列式,如果D的第行所有 元素除☑,外,其余元素均为零,那么行列式D等 于与其代数余子式的乘积,即
二.行列式按行(列)展开定理 引理 设D为n阶行列式,如果D的第i行所有 元素除 外,其余元素均为零,那么行列式D等 于 与其代数余子式的乘积,即 aij ij a D = aijAij

证:设 03 a : D 0
证:设 n n j n n i j j n a a a a a a a D 1 1 1 1 1 = 0 0

0 a ● =(1 i-1 -1n d,r 7+1 i+In 。 an
( ) n n j n n i i j i n i i j i n j n i j i a a a a a a a a a a a a a 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 + + + − − − − = −

00 =(←1(-1 a-1 0-1 01j i-1j+ -In + =(-1arMi=aj4
( ) ( ) ( ) i j i j i j i j i j n j n n j n j n n i j i i j i j i n i j i i j i j i n j j j n i j i j a M a A a a a a a a a a a a a a a a a a a a a a a = − = = − − + − + + + + − + + + − − − − − + − − + − − 1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

定理1行列式等于它的任一行(列)的各元素与其对 应的代数余子式乘积之和,即 (i12,n D=a)A,+a,4,++Q (j=1,2,…,n)
D a A a A a A = + + + i i i i in in 1 1 2 2 1,2, , . (i n = ) ( ) 1 1 2 2 1,2, , . D a A a A a A j j j j nj nj j n = + + + = 定理1 行列式等于它的任一 行(列)的各元素与其对 应的代数余子式乘积之和,即

证: aji aj2 D 二 ai2 a n2
证: n n n n i i i n n a a a a a a a a a D 1 2 1 2 1 1 1 2 1 =
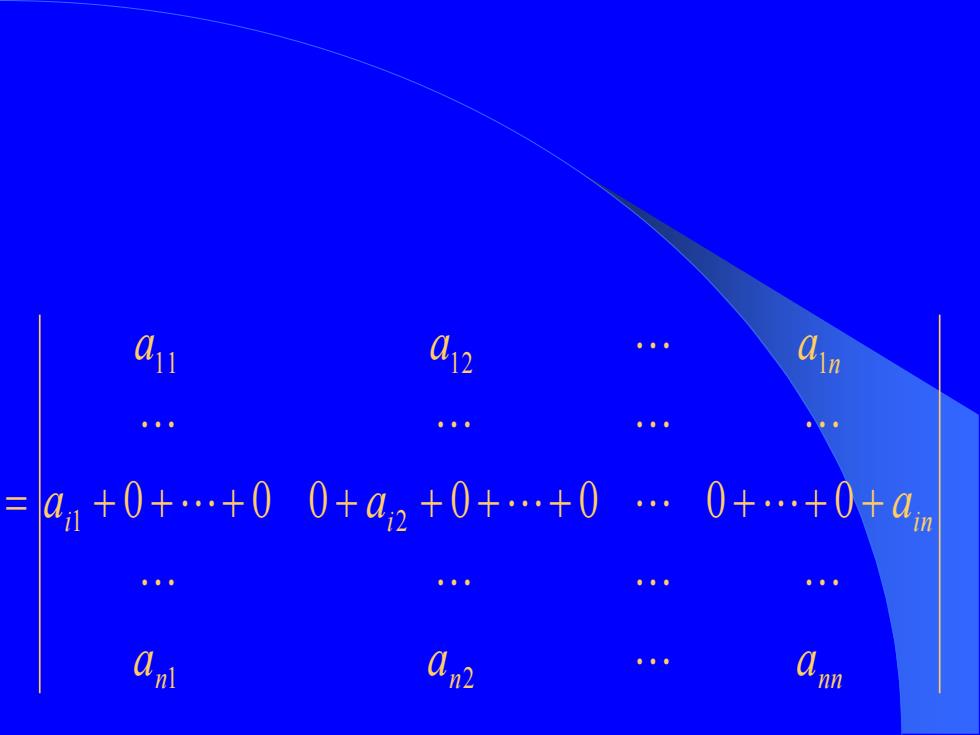
0 02 0 1+0++00+a2+0++00+…+0+a 0 0 a n
n n n n i i i n n a a a a a a a a a 1 2 1 2 1 1 1 2 1 = + 0 + + 0 0 + + 0 + + 0 0 + + 0 +
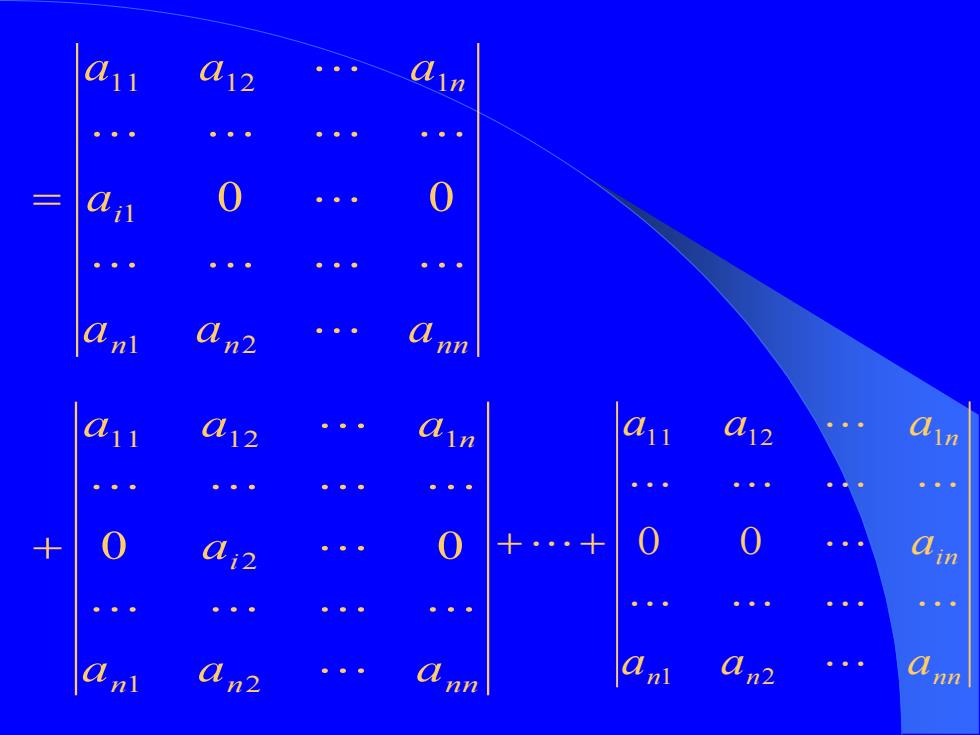
d12 。。 A n2 nn d12 。。 。。中 a n2 nn
n n n n i n a a a a a a a 1 2 1 1 1 1 2 1 = 0 0 n n n n i n a a a a a a a 1 2 2 1 1 1 2 1 + 0 0 n n n n i n n a a a a a a a 1 2 1 1 1 2 1 + + 0 0