
例3 证明范蒙得(Vandermonde)行列式 K, =Πk-x, ) .: n21>2] x X2 其中记号“Π”表示全体同类因子的乘积
例3 证明范蒙得(Vandermonde)行列式 ( ), 1 1 1 1 1 1 2 1 1 2 2 2 2 1 1 2 i j n i j n n n n n n n x x x x x x x x x x x D = = − − − − 其中记号“Π”表示全体同类因子的乘积. (1)

证:用数学归纳法因为 22i>j2 所以当n=2时(1)成立 现在假设(1)对于n一l阶Vandermonde行列式,即 X2 几-x, 21>j22
所以当n=2时(1)成立. 现在假设(1)对于n-1阶Vandermonde行列式,即 ( ) i j n i j n n n n n n x x x x x x x x D = = − − − − − 2 2 2 3 2 2 2 3 1 1 1 1 证: 用数学归纳法.因为 ( ) i j i j x x x x x x D = = − = − 2 1 2 1 1 2 2 1 1

我们来证明对n阶Vandermonde行列式也成立 0 X-X X3- X-X D=0x6-x)3-x 0x3-x)3-x)…x-x)
我们来证明对n阶Vandermonde行列式也成立. ( ) ( ) ( ) ( ) ( ) ( )1 2 3 1 2 2 1 3 2 2 2 2 1 3 3 1 1 2 1 3 1 1 0 0 0 1 1 1 1 x x x x x x x x x x x x x x x x x x x x x x x x D n n n n n n n n n − − − − − − − − − = − − −

n-2 n- =(x2-x;-x)..x)I, n2i>≥2 =I(x,-x, n≥i>≥1
( )( ) ( ) 2 2 3 2 2 2 3 2 1 3 1 1 1 1 1 − − − = − − − n n n n n n x x x x x x x x x x x x ( )( ) ( ) 2 1 3 1 1 x x x x x x = − − n − ( ) i j n i j x − x 2 ( ) i j n i j = x − x 1

例4.计算 2 3 5 D 22 =12 32 42 52 23 33 43 5
12 2 3 4 5 2 3 4 5 2 3 4 5 1 1 1 1 3 3 3 3 2 2 2 2 D = = 例4.计算

三、行列式展开定理的推论 推论 行列式某一行(列)的元素与另一行 (列)的对应元素的代数余子式乘积之和等于零 即 0n4n+a242++0n4m=0i≠j月 或 aAy +azA+am A=0i
三、行列式展开定理的推论 推论 行列式某一行(列)的元素与另一行 (列)的对应元素的代数余子式乘积之和等于零. 即 0, , 1 1 2 2 a A a A a A i j i j i j i n j n + ++ = 或 0, , 1 1 2 2 a A a A a A i j i j i j n i n j + ++ =
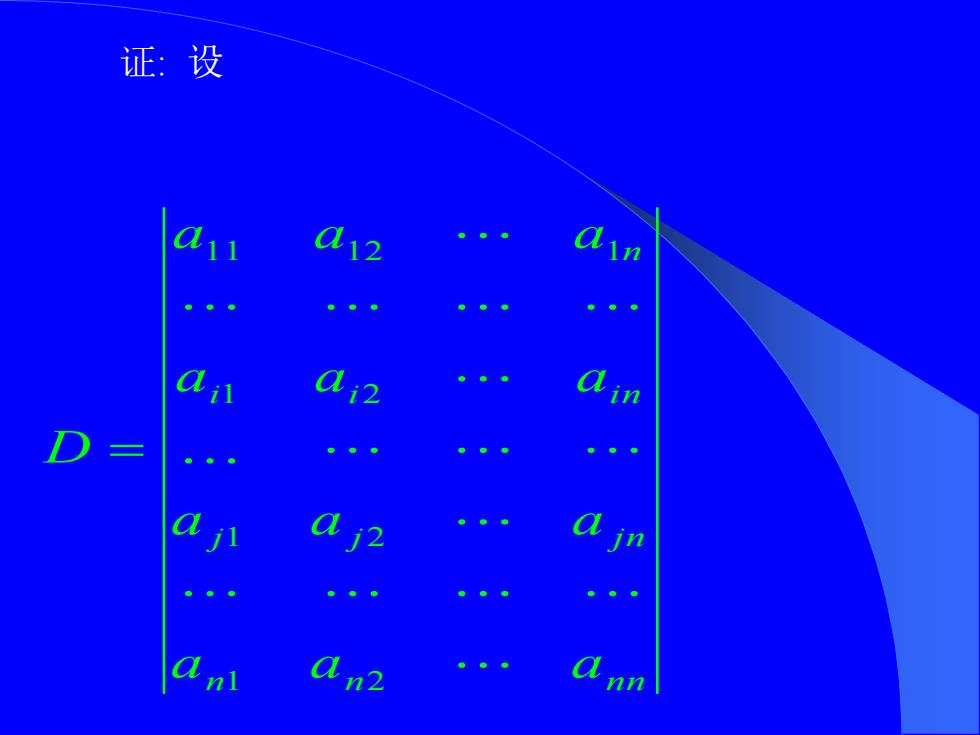
证:设 d12 an an?
证: 设 n n n n j j j n i i i n n a a a a a a a a a a a a D 1 2 1 2 1 2 1 1 1 2 1 =

把D按第行展开,有 C12 an2 =an+a242+…+an4n
把D按第j行展开,有 n n n n j j j n i i i n n a a a a a a a a a a a a 1 2 1 2 1 2 1 1 1 2 1 j j j j j nAj n = a A + a A ++ a 1 1 2 2

在上式两端用 a12y…,☑m 代替 1,j2,…,☑m得 in an2 nn =an4+a2A2+…+anAn(t≠j)
在上式两端用 a i 1 , a i 2 , , ai n 代替 , , , , a j 1 a j 2 aj n 得 n n n n i i i n i i i nn a a a a a a a a a a a a 1 2 1 2 1 2 1 1 1 2 1 i j i j i n Aj n = a A + a A + + a 1 1 2 2 ( i j )

显然,等式左端行列式有两行相同,故行列式等于零,即 a1A1+a2At…+amAm=0,i≠j, 同理可证, a4y+a,42+…+Am An=0,i≠j
同理可证, 0, , 1 1 2 2 a A a A a A i j i j + i j ++ i n j n = 0, , 1 1 2 2 a A a A a A i j i j + i j ++ n i n j = 显然,等式左端行列式有两行相同,故行列式等于零,即