
§2.矩阵的运算 、 矩阵的加法 1、定义 定义 2设有两个mXn矩阵A=(a,),B=(亿,) 那末矩阵A与B的和记作A+B,规定为 a1+b1 a2+62 a21+b1 A22+b23 A+B三 am+bm am2+6m2 矩阵的减法:A-B=A+(一B
§2.矩阵的运算 一、矩阵的加法 1、定义 定义2 设有两个m×n矩阵 A B 那末矩阵 A 与 B 的和记作 A + B , 规定为 ( ), ( ) = ai j = bi j A + B = + + + + + + + + + m m m m m n m n n n n n a b a b a b a b a b a b a b a b a b 1 1 2 2 2 1 2 1 2 2 2 2 2 2 1 1 1 1 1 2 1 2 1 1 矩阵的 减法:A – B = A + (-B )

2、运算律 矩阵的加法满足下列运算规律设A、 B、C都是mXn矩阵 1)A+B=B+A 2)(A+B)+C=A+(B+C) 3)A+(一A)=A一A=0 二、数与矩阵相乘 1、定义 定义3 数入与矩阵的乘积记作4或A几,规定为 xavi 入a12 MA=AI- 入a22 7入d2n 。。 。。
2、运算律 矩阵的加法满足下列运算规律设 A、 B、C 都是 m×n 矩阵: 1) A + B = B + A 2)(A + B)+ C = A +( B + C ) 3) A +(-A)= A- A = 0 二、数与矩阵相乘 1、定义 定义3 数 λ 与矩阵的乘积,记作 λA 或Aλ,规定为 λA = A λ= m m mn n n a a a a a a a a a 1 2 2 1 2 2 2 1 1 1 2 1

2、运算律 数乘矩阵满足下列运算规律 设A、B为mXn矩阵,入、u为数: 1)(2)A=元(A) 2) ()+u)A=人A+A: 3) λ(A+B)=A+λB 这样定义矩阵加法和数乘矩阵的运算,统称为 矩阵的线性运算
2、运算律 数乘矩阵满足下列运算规律 设 A、B 为 m×n 矩阵,λ、μ为数: 2) ( λ + μ ) A = λ A + μA; 1) (λμ)A = λ ( μA ) 3) λ ( A + B ) = λA + λB 这样定义矩阵加法和数乘矩阵的运算,统称为 矩阵的线性运算

三、矩阵与矩阵相乘 1、定义 定义4设A=(a,mX,B=(b,)x矩阵, 那末规定矩阵A与矩B的乘积是一个m×n矩阵 C=(c)mXm。其中 cy=anby+ab,+…+ab 2abg6=1,2…m,j=1,2m 即 AXB=C
三、矩阵与矩阵相乘 1、定义 定义4 设 A =(aij)m×s , B = ( bij )s×n 矩阵, 那末规定矩阵 A与矩 B 的乘积是一个m×n矩阵 C = ( c ij )m×n 。其中 即 A× B = C. 1 ( 1,2, ; 1,2 ), s ik kj k a b i m j n = = = = ij i j i j is sj 1 1 2 2 c a b a b a b = + + +

注意: (a1a2 b anby,apbj+.+aiby anby cu
注意: kj i j s k = ai kb = c =1 ( ) 1 2 1 2 j j i i is sj b b a a a b = + + + a b a b a b i j i j is sj 1 1 2 2
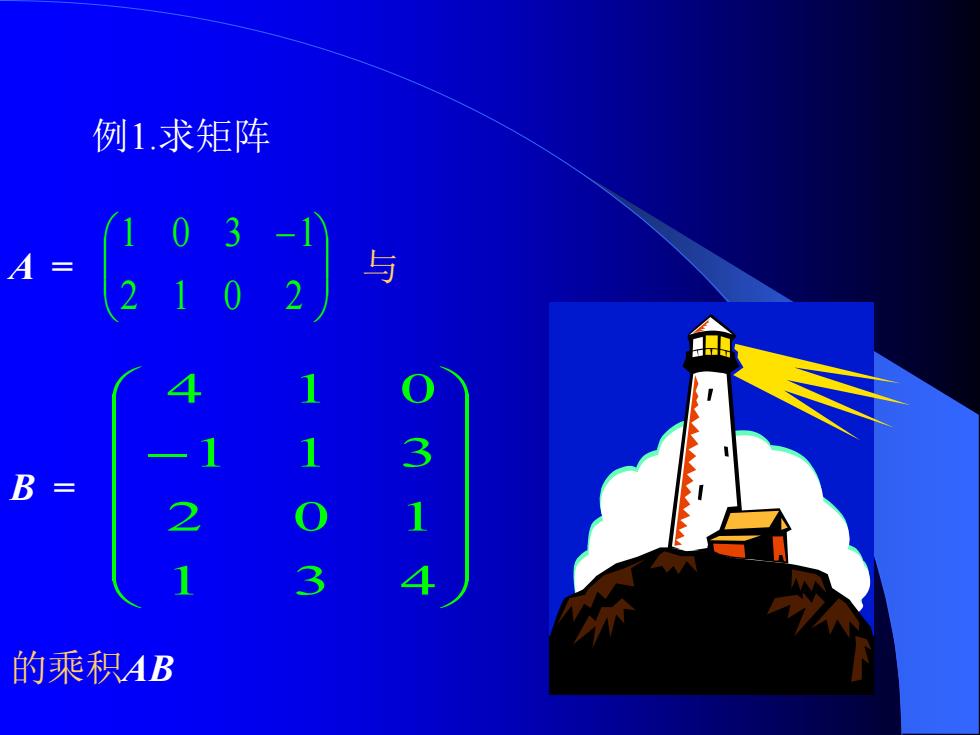
例1.求矩阵 a-68 与 B= 3 的乘积AB
例1.求矩阵 − 2 1 0 2 1 0 3 1 − 1 3 4 2 0 1 1 1 3 4 1 0 A = B = 与 的乘积AB
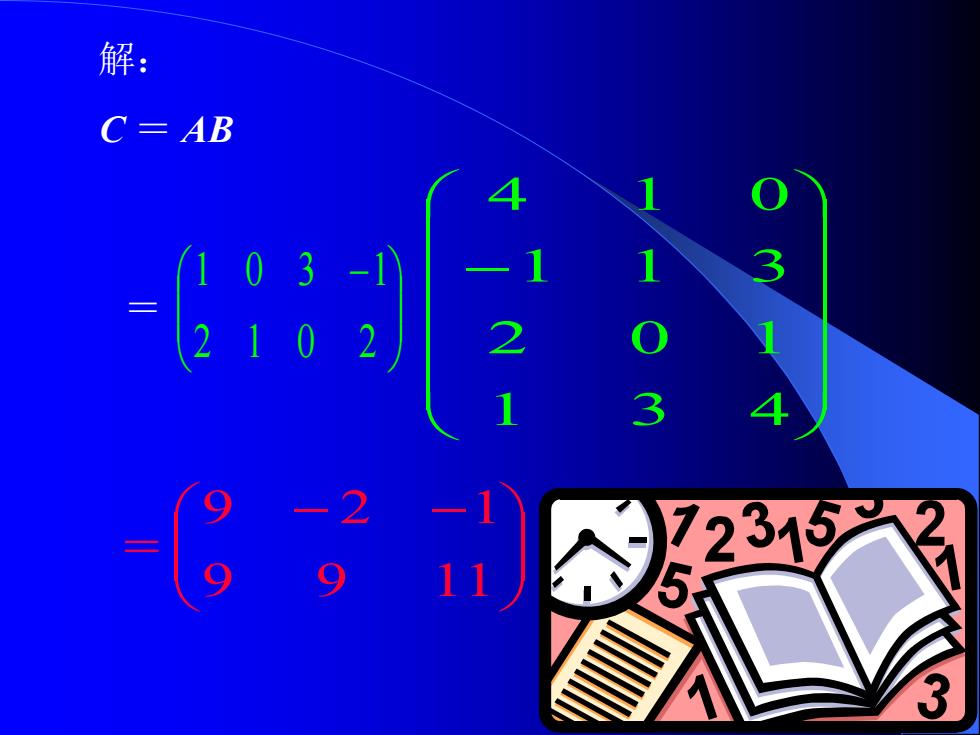
解: C=AB - 2 3 0
C = AB − 2 1 0 2 1 0 3 1 − 1 3 4 2 0 1 1 1 3 4 1 0 − − = 9 9 11 9 2 1 解: =

例2.设矩阵 -2 求AB与BXA
例2. 设矩阵 − − 1 2 2 4 −3 − 6 2 4 A = B = 求AB与B×A

解: AB- 刘 16
AB = − − 1 2 2 4 −3 − 6 2 4 − − = 8 16 16 32 −3 − 6 2 4 − − 1 2 2 4 = 0 0 0 0 解: BA=
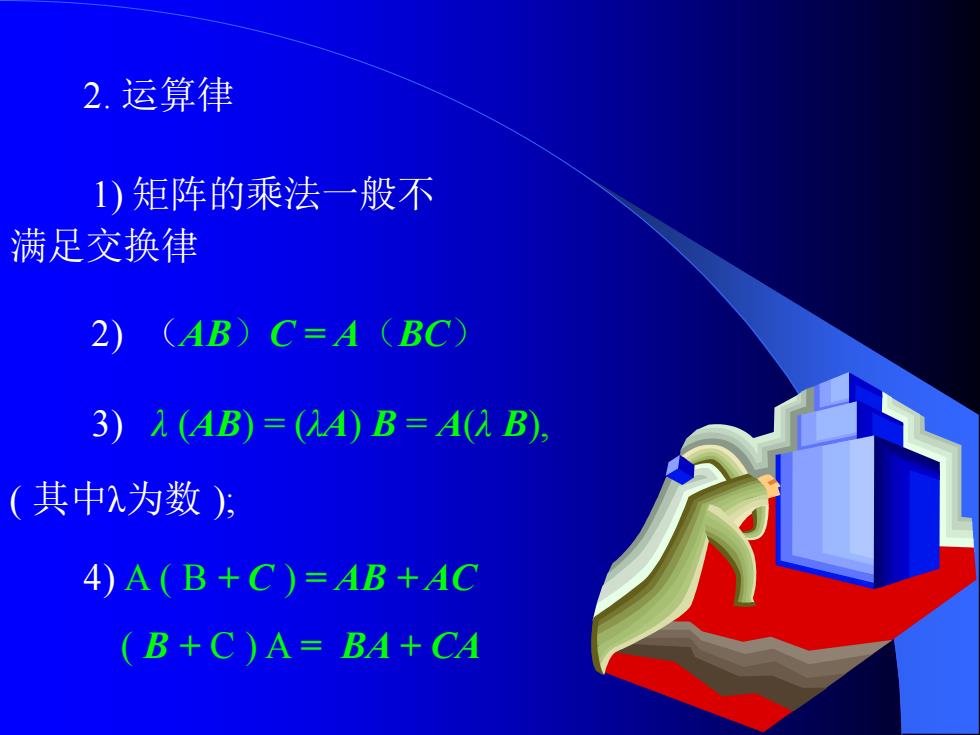
2.运算律 1)矩阵的乘法一般不 满足交换律 2) (AB)C=A (BC) 3)1(AB)=(A)B=A(B) (其中,为数)方 4)A(B+C)=AB+AC (B+C)A=BA+CA
2. 运算律 1) 矩阵的乘法一般不 满足交换律 2) (AB)C = A(BC) 3) λ (AB) = (λA) B = A(λ B), ( 其中λ为数 ); 4) A ( B + C ) = AB + AC ( B + C ) A = BA + CA