
x1-x3=4 从而得等价的方程组 x2-X3=3 x4=-3 取x3为自由未知量,并令X3=C,即得 X3 X= C+3 X3 XA 其中c为任意常数
从而得等价的方程组 = − − = − = 3 3 4 4 2 3 1 3 x x x x x 取 x3 为自由未知量,并令 x3 = c , 即得 x = 4 3 3 1 x x x x − + + = 3 3 4 c c c − + = 3 0 3 4 0 1 1 1 c 其中c为任意常数

1 1)行阶梯形矩阵: 2)行最简形矩阵: ※一个矩阵的行最简形矩阵是唯一的 要解线性方程组只须把增广矩阵化为行最 简形矩阵
1) 行阶梯形矩阵: − − − 0 0 0 0 0 0 0 0 1 3 0 1 1 1 0 1 1 2 1 4 2) 行最简形矩阵: − − − 0 0 0 0 0 0 0 0 1 3 0 1 1 0 3 1 0 1 0 4 ※ 一个矩阵的行最简形矩阵是唯一的. 要解线性方程组,只须把增广矩阵化为行最 简形矩阵
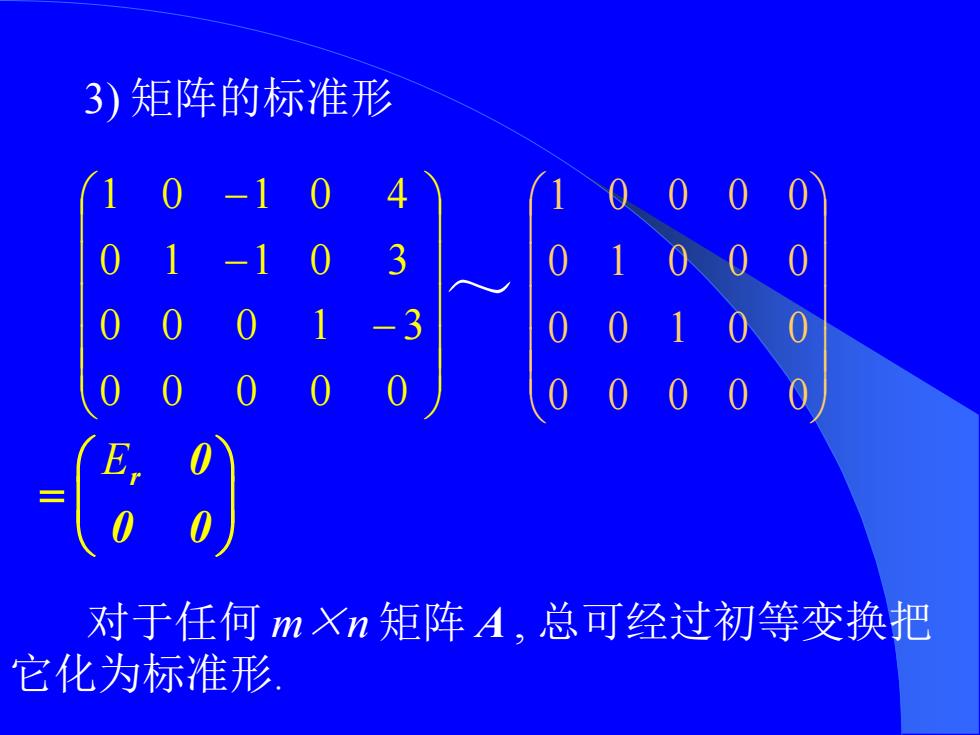
3)矩阵的标准形 对于任何mn矩阵A,总可经过初等变换把 它化为标准形
3) 矩阵的标准形 − − − 0 0 0 0 0 0 0 0 1 3 0 1 1 0 3 1 0 1 0 4 ~ 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 对于任何 m×n 矩阵 A , 总可经过初等变换把 它化为标准形. r 0 0 0 = E

r- mxn 此标准形由m、n、r三个数完全确定,其中r就是行 阶梯形矩阵中非零行的行数.所有与A等价的矩阵组成的集 合,称为一个等价类,标准形F是这个等价类中形状最简单的 矩阵 例2设 求A的标准形
此标准形由 m、n、r 三个数完全确定 , 其中 r 就是行 阶梯形矩阵中非零行的行数.所有与A等价的矩阵组成的集 合,称为一个等价类,标准形F是这个等价类中形状最简单的 矩阵. 例2 设 求A的标准形。 0 0 0 = r m n E F 3 2 0 1 0 2 2 1 1 2 3 2 0 1 2 1 A − − = − − −

解: 3 -2 2 0
解: ~ ~ ~ 3 2 0 1 0 2 2 1 1 2 3 2 0 1 2 1 A − − = − − − 1 2 3 2 0 2 2 1 3 2 0 1 0 1 2 1 − − − − − 1 2 3 2 0 2 2 1 0 4 9 5 0 1 2 1 − − − 1 0 0 0 0 2 2 1 0 4 9 5 0 1 2 1

0
~ 0 4 9 5 0 2 2 1 0 1 2 1 1 0 0 0 − − 0 0 5 3 0 0 2 1 0 1 2 1 1 0 0 0 ~ − − 0 0 5 3 0 0 2 1 0 1 0 0 1 0 0 0 ~ − − 0 0 3 5 0 0 1 2 0 1 0 0 1 0 0 0 ~
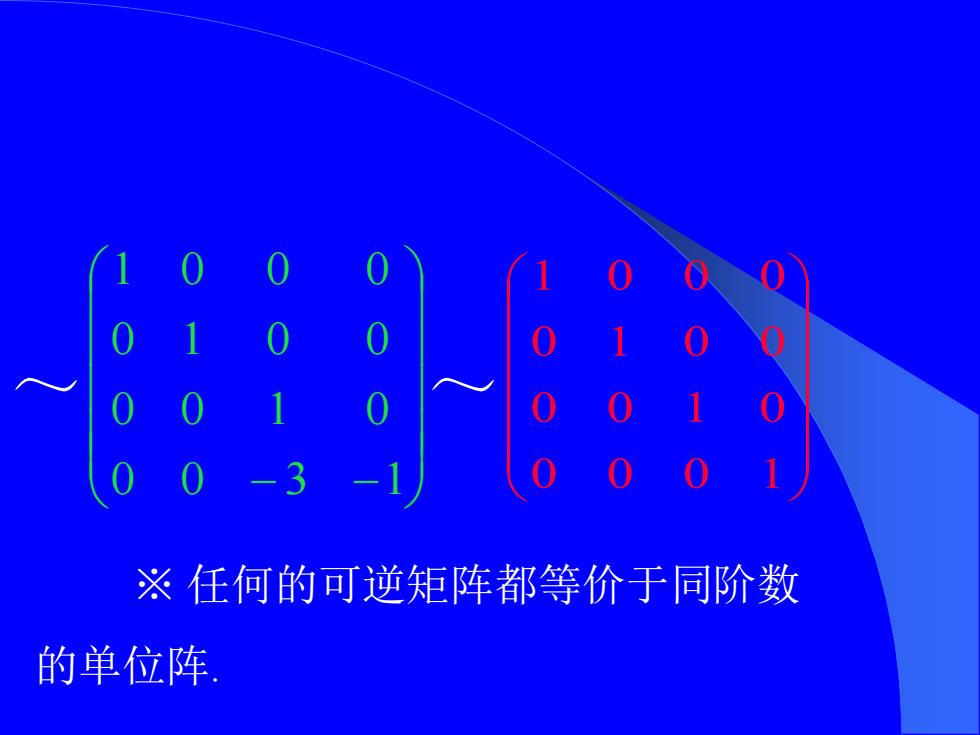
※任何的可逆矩阵都等价于同阶数 的单位阵
~ 0 0 − 3 −1 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 ~ ※ 任何的可逆矩阵都等价于同阶数 的单位阵

练习 把下列矩阵化为行最简形矩阵: 2 1) 2 3 -4 3 -3 5 一4 (2) 2 -2 3 -2 3 -34 -2
练习 ( ) − 3 0 4 3 2 0 3 1 1 0 2 1 1 . ( ) − − − − − − − − − 3 3 4 2 1 2 2 3 2 0 3 3 5 4 1 1 1 3 4 3 2 . 把下列矩阵化为行最简形矩阵: