
向量空间的基与维数 定义9设V为向量空间,如果r个向量a1,a2,,a, ∈V,且满足 (1)a1,a2,,a,线性无关 (2)V中任一向量都可由a1,a2,,a,线性表示, 那末,向量组a1,a2,,a,就称向量空间V的一个基,r称为 向量空间V的维数,并称V为r维的向量空间 1、如果向量空间V没有基,那末V的维数为0。 2、0维的向量空间只含有一个零向量0。 3、若把向量空间V看作向量组,则V的基就是向量组 的极大无关组,V的维数就是向量组的秩
二、向量空间的基与维数 定义9 设V为向量空间,如果 r 个向量 α1 , α2 ,…, αr ∈V , 且满足 (1) α1 , α2 ,…, αr 线性无关; (2) V中任一向量都可由α1 , α2 ,…, αr 线性表示, 那末,向量组α1 , α2 ,…, αr 就称向量空间V的一个基,r 称为 向量空间V的维数,并称V为r 维的向量空间。 1、如果向量空间V没有基,那末V的维数为0。 2、0维的向量空间只含有一个零向量0。 3、若把向量空间V看作向量组,则V的基就是向量组 的极大无关组,V的维数就是向量组的秩

4、V0={化=(0,x2,,xn)I|x2,,xm∈R}的一个基为: 。 所以V是一个n一1维的向量空间。 5、由向量组a1,a2,,an所生成的向量空间 V={x=1a1+2a2+…+2mam|九1,2,,m∈R}。 显然,向量空间V与向量组a1,a2,,am等价,所以向量组 a1,a2,,am的极大无关组就是V的一个基,a1,a2,,am的秩 就是V的维数
4、V0 = {x = (0, x2 , …, xn ) T | x2 ,…, xn ∈R}的一个基为: 2 0 0 1 0 , , 0 1 n e e = = 所以V0是一个n-1维的向量空间。 5、由向量组α1 ,α2 ,…,αm所生成的向量空间 V = { x = λ1α1 + λ2α2 + … +λmαm | λ1 , λ2 , …, λm ∈ R }。 显然,向量空间V与向量组 α1 , α2 ,…, αm 等价,所以向量组 α1 ,α2 ,…,αm 的极大无关组就是V的一个基, α1 ,α2 ,…,αm 的秩 就是V的维数

、若向量空间VcR”,则V的维数不会超过n。并且, 当V的维数为n时,V=Rn。 Z、若向量组a1,a2,,a,是向量空间V的一个基,则 V可表示为 V={x=1a1+202++2,a,|1,2,,1,∈R}。 这就清楚地显示出一个向量空间V的构造
6、若向量空间V⊂Rn ,则V的维数不会超过 n 。并且, 当 V 的维数为 n 时,V = Rn 。 7、若向量组 α1 ,α2 ,…,αr 是向量空间 V 的一个基,则 V 可表示为 V = { x = λ1α1 + λ2α2 + … +λrαr | λ1 , λ2 , …, λr ∈ R }。 这就清楚地显示出一个向量空间V的构造
例6设 A=(a1,a,a3)=2 B=(b1,b2)= —a心 验证a1,a2,a3是R的一个基,并把b1,b2用这个基线性表示 解 要证a1,a2,a3是R的一个基,只需证a1,a2,a3线性 无关,即证AE即可
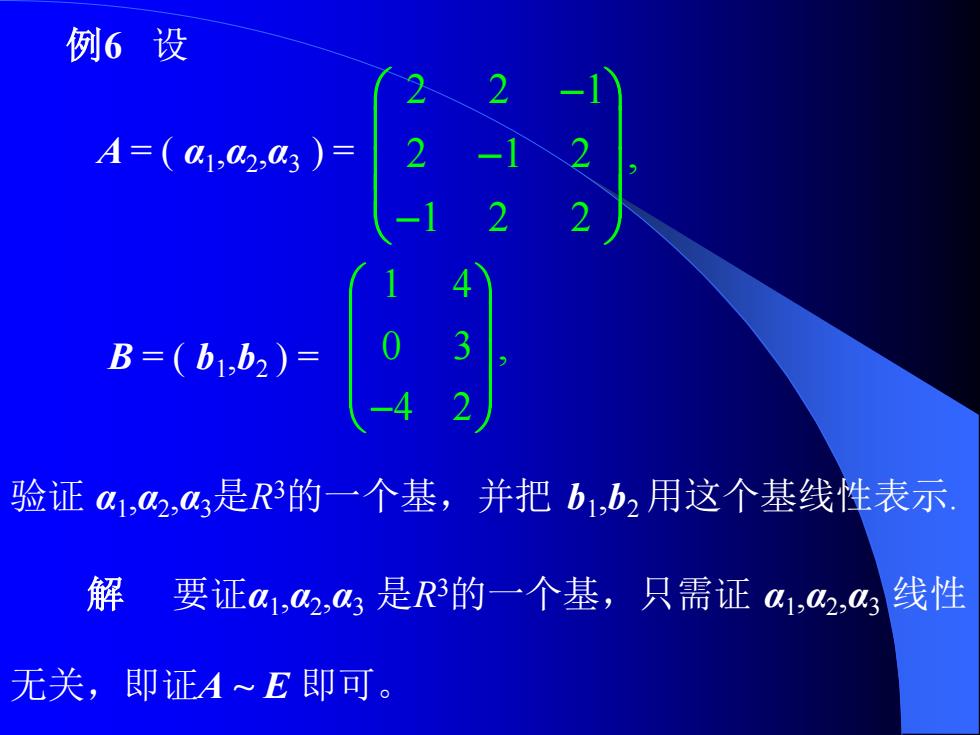
例6 设 A = ( α1 ,α2 ,α3 ) = 2 2 1 2 1 2 , 1 2 2 − − − B = ( b1 ,b2 ) = 1 4 0 3 , 4 2 − 验证 α1 ,α2 ,α3是R3的一个基,并把 b1 ,b2 用这个基线性表示. 解 要证α1 ,α2 ,α3 是R3的一个基,只需证 α1 ,α2 ,α3 线性 无关,即证A ~ E 即可

设b1=x11a1+x22+X31a3 b2=X12a1+X2202+X3203 即 (b1,b2)=(a1,a2,a3) X31 X32 记作B=AX。 对矩阵(AB)施行初等行变换,若A能变为E,则 a1,a2,a为R的一个基,且当A变成E时,B变为X=AlB 2-114 (AB)= 2 -1 2 03 -1 2 2 2
设 b1 = x11α1+x21α2+x31α3 b2 = x12α1+x22α2+x32α3 即 ( b1 ,b2 )= (α1 ,α2 ,α3 ) 11 12 21 22 31 32 , x x x x x x 记作 B = AX。 对矩阵(A|B)施行初等行变换,若 A 能变为 E,则 α1 ,α2 ,α3为R3的一个基,且当 A变成 E 时,B 变为X = A-1B. ( A|B ) = 2 2 1 1 4 2 1 2 0 3 1 2 2 4 2 − − − −

11 3 0-3 -3 03 5 1 .3 2 -3 2 3 3 2-3
1 1 1 1 3 0 3 0 2 3 0 3 3 5 5 − − − − 1 1 1 1 3 0 3 0 2 3 0 0 3 3 2 − − − − 1 1 1 1 3 2 0 1 0 1 3 2 0 0 1 1 3 − − − 7 1 1 0 0 3 2 0 1 0 1 3 2 0 0 1 1 3 − − 2 4 1 0 0 3 3 2 0 1 0 1 . 3 2 0 0 1 1 3 − −

显然,AE,故a1,a2,a3 是R3的一个基,且 2-3 4 3 (b1,b2)=(a1,a2,a3) 2- -1 2一
显然,A ~ E,故 α1 ,α2 ,α3 是 R3 的一个基,且 ( b1 ,b2 )= (α1 ,α2 ,α3 ) 2 4 3 3 2 1 . 3 2 1 3 − −

三、过渡矩阵与坐标变换 1、过渡矩阵 设n维向量空间V的两组基为 A:a1,a2,an B:f1,2,…,fn 由于A组基与B组基等价,所以 [B=C1a+C21a2+…+CmC 阝2=C2C+C22C2++Cn2C B=cuna C2ndz++Cmnn
三、过渡矩阵与坐标变换 1、过渡矩阵 设n维向量空间V的两组基为 A : α1 , α2 , … , αn B : β1 , β2 ,… , βn 由于A组基与B组基等价,所以 1 11 1 21 2 1 2 12 1 22 2 2 1 1 2 2 = + + + = + + + = + + + n n n n n n n nn n c c c c c c c c c

即p1,2,,阝n)=(a1,a2,,an)C 称矩阵C为由基a1,a2,,an到基阝1,P2,,Bm 的过渡矩阵。其中 1 22 C2n Cn2 C m
即(β1 , β2 ,… , βn ) = (α1 , α2 , … , αn )C. 称矩阵 C 为由基α1 , α2 , … , αn到基 β1 , β2 ,… , βn 的过渡矩阵。其中 C = 11 12 1 21 22 2 1 2 n n n n nn c c c c c c . c c c
