吉林大学：《线性代数》课程教学资源（PPT课件）第五章 相似矩阵及二次型 48-5-3 §3 相似矩阵

例1求一可逆矩阵P,把 -2 11 A= -41 化成对角矩阵 解①由4一E=0,求A的全部特征值 -2-入1 A-入E 2-入0 -4 13-入 =(2-入)22-入-2) =-(入+102-2)2 所以4的特征值为入=-1，入2=入3=2

例1 求一可逆矩阵P,把           − − = 4 1 3 0 2 0 2 1 1 A 化成对角矩阵. 解 ①由|A－λE|=0,求A的全部特征值. − −  −  − −  −  = 4 1 3 0 2 0 2 1 1 A E − −  − −  = −  4 3 2 1 (2 ) (2 )( 2) 2 = −  − − 2 = −( +1)( − 2) 1, 2. 所以A的特征值为 = − 2 = 3 =

②由(A-入E)x=0,求A的特征向量 当入，=-时，解方程(A+E)x=0由 : 得基础解系P 当)2=入3=2时，解方程(A-2E)x=0由 -41 -411 A-2E= 0 0 0 0 -4 1 0 0

② 由(A−E)x = 0,求A的特征向量. 当1 = −1时,解方程(A+ E)x = 0.由           − − + = 4 1 4 0 3 0 1 1 1 A E ～           − 0 0 0 0 1 0 1 0 1 当2 = 3 = 2时,解方程(A− 2E)x = 0.由           − − − = 4 1 1 0 0 0 4 1 1 A 2E ～          − 0 0 0 0 0 0 4 1 1 . 1 0 1 1           得基础解系P =

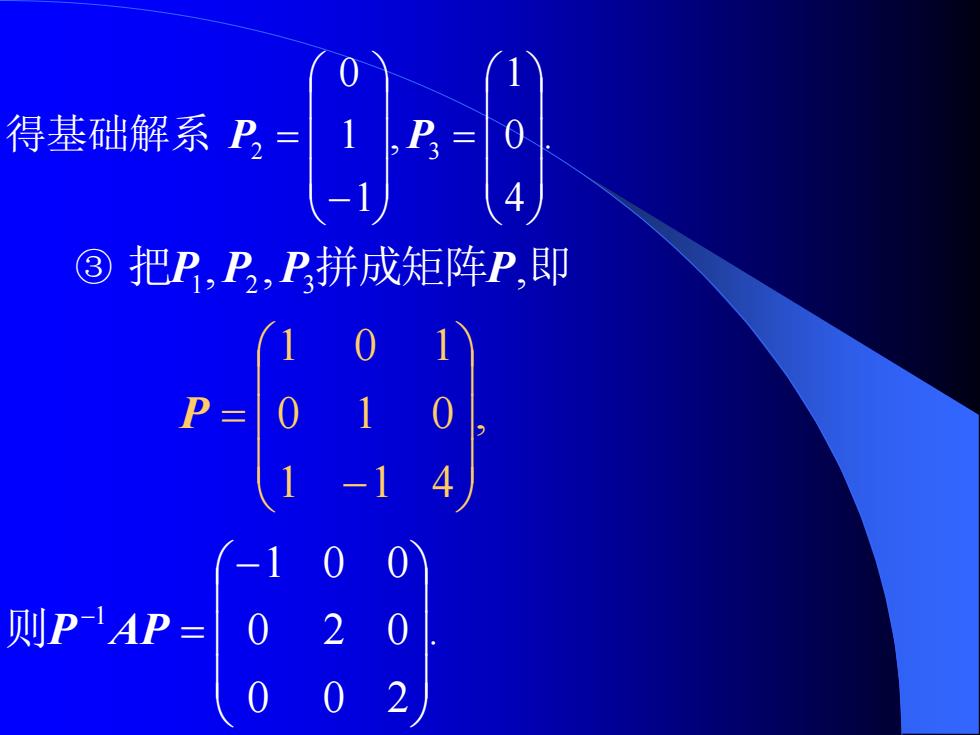
得基础解系P ③把P,卫，P拼成矩阵P,即 -1 则PAP= 2

. 4 0 1 , 1 1 0 2 3           =           − 得基础解系 P = P ③ 把P1 , P2 , P3 拼成矩阵P,即 , 1 1 4 0 1 0 1 0 1           − P = . 0 0 2 0 2 0 1 0 0 1          − = − 则P AP

例2设矩阵A与B相似，其中 -20 0 (1)求x和的值，(2)求可逆矩阵P,使PAP=B 解(I)因为A∽B,所以B的主对角线元素是A的特征值 因此有 -2+x+1=-1+2+y A-入E=A+E=0

例2 设矩阵A与B相似,其中 , 3 1 1 2 2 2 0 0          − A = x . 0 0 0 2 0 1 0 0          − = y B （1）求x和y的值, 解 (1)因为A∽B,所以B的主对角线元素是A的特征值. 因此有     = + = − + + = − + + 0 2 1 1 2 A- E A E x y (2) , . 1 P P AP = B 求可逆矩阵 使 −

x-y=2 x=0 整理得 解得 x=0 y=-2 (2)由于A∽B,所以A的特征值为=-1，入2=2，入3=-2. 由(A-入Ex=0,求A的特征值 当入=-时 -10 0 00 A+E= 212 2 31 2 得基础解系：P= 2

(2) 由于A∽B,所以A的特征值为 1, 2, 2. 1 = − 2 = 3 = − 由(A- E)x = 0,求A的特征值. 当1 = −1时          − + = 2 2 1 0 3 1 2 1 0 A E ～           0 2 1 0 0 0 0 1 0 得基础解系: , 1 2 0           − P1 = , 0 2    = − = x x y 整理得 . 2 0    = − = y x 解得

当2=2时， -40 A-2E= 得基础解系：卫= 1 当入3=-2时 12a2之2、910 -1 得基础解系：P三 3 1

～ , 0 1 1 0           − 0 0 0 1 0 得基础解系: , 1 1 0           P2 = 当3 = −2时           + = 3 2 0 0 2 3 1 2 2 0 A E ～ , 0 0 1 1           0 0 0 1 0 得基础解系: , 1 0 1          − P3 =           − − − − = 1 2 2 4 0 2 3 1 2 0 A E 当λ2 ＝2时

令可逆矩阵 P=(P,P2,P)= 2 即为所求 例3设矩阵 3 2 一2 A= 4 2

令可逆矩阵           − − = = 1 1 1 2 1 0 0 0 1 ( , , ) P P1 P2 P3 即为所求. 例3 设矩阵           − − − − = 4 2 3 1 3 2 2 A k k

问当k为何值时，存在可逆矩阵P,使得P1AP为对角阵，并求 出P和相应的对角阵。 解由 -入 A-入E 2 -1 入+1 入+1 =(久+1)2（久-1）=0 得A的特征值为：入1=入2=-1，入3=1

问当k为何值时,存在可逆矩阵P,使得P-1AP为对角阵，并求 出 P和相应的对角阵。 解 由 − −  − − −  −  −  = 4 2 3 1 3 2 2 A- E k k 0 0 1 0 1 1 2 2  +  + −  − − = k ( 1) ( 1) 0 2 =  +  − = : 1, 1. 得A的特征值为 1 = 2 = − 3 =

对于入1=入2=-1时，有 当k=0时，上式变为 0 0 对应特征向量可取为： 1三 2

对于1 = 2 = −1时,有 ～           − − 0 0 0 0 4 2 2 k k 当k = 0 时,上式变为          − − 0 0 0 0 0 0 4 2 2 ～               − 0 0 0 0 0 0 2 1 2 1 1 对应特征向量可取为: 4 2 2 ( 0 4 2 2 A E   −   + = −      − λ ) k k 1 2 1 1 2 , 0 . 0 2 p p     −     = =            

对于)，=时，有 2 (A-E)= -2 4 2 对应特征向量可取为

对于3 =1时,有           − − − − − = 4 2 4 2 2 2 2 (A E) k k ～           − − − − 0 2 0 2 1 1 1 k k ～           − 0 0 0 0 1 0 1 0 1 对应特征向量可取为: . 1 0 1 3           P =