
P-AP=∧ 其中对角矩阵Λ的对角元素含个入,2个入2,…,个入, 恰是A的m个特征值 4 例1设 A 求一个正交矩阵P,使PAP=人为对角矩阵 解①由4一入E=0,求A的全部特征值. 4-入0 0 A-入E 3-入1 =(4-入)22-6入+8) 13-入
. 1 = − P AP , , , , 1 1 2 2 s s 其中对角矩阵的对角元素含r个 r 个 r 个 恰是A的n个特征值. 例1 设 , 0 1 3 0 3 1 4 0 0 A = , . 求一个正交矩阵P 使P −1 AP = 为对角矩阵 解 ①由|A-λE| = 0 , 求 A 的全部特征值. − − − − = 0 1 3 0 3 1 4 0 0 A E (4 )( 6 8) 2 = − − +

=2-入(4-入)2=0 得A的特征值为入,=2,入2=入,=4 (2)由(A-入E)x=0,求A的特征向量当)=2时,由 x 解得 k0任意 取c
(2 )(4 ) 0 2 = − − = 2, 4. 得A的特征值为1 = 2 = 3 = (2).由(A−E)x = 0,求A的特征向量.当1 = 2时,由 , 0 0 0 0 1 1 0 1 1 2 0 0 3 2 1 = x x x , 1 1 0 1 3 2 1 − = k x x x 解得 k1≠0任意. , 1 1 0 1 − 取c = . 1 1 0 2 1 1 − 单位化p =
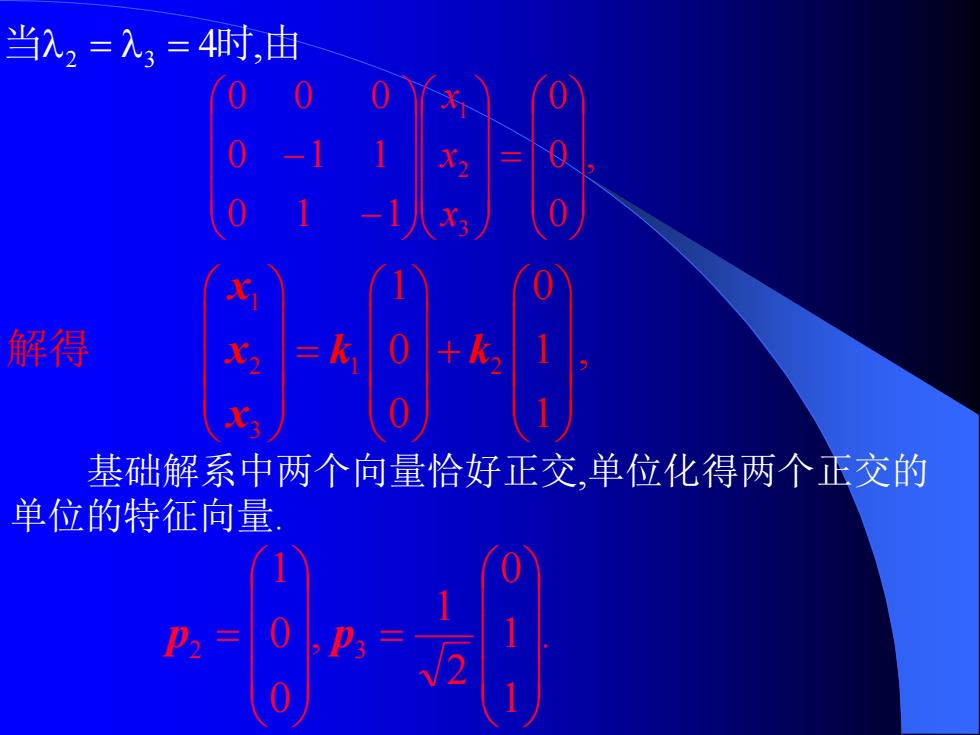
当入2=入3=4时,由 解得 =k0 k, 基础解系中两个向量恰好正交,单位化得两个正交的 单位的特征向量
当2 = 3 = 4时,由 , 0 0 0 0 1 1 0 1 1 0 0 0 3 2 1 = − − x x x 基础解系中两个向量恰好正交,单位化得两个正交的 单位的特征向量. . 1 1 0 2 1 , 0 0 1 2 3 = p = p 1 2 1 2 3 1 0 0 1 , 0 1 x x k k x = + 解得

(3)将求得的pP2,拼成一个正交矩阵P即 P=(P,P2,P3) 51万 (4)可以验知确有 P-AP=PAP
(4)可以验知确有 . 0 0 4 0 4 0 2 0 0 1 T = = − P AP P AP 1 2 3 0 1 0 1 1 ( , , ) . 0 2 2 1 1 0 2 2 P p p p = = − 1 2 3 p p p P (3) , , . 将求得的 拼成一个正交矩阵 即

在此例中对应于λ=4,若求得方程(A一入E)x=0的基 础解系 6 则测需把它施密特标准正交化: I
在此例中对应于λ=4,若求得方程(A- λ E) x = 0 的基 础解系 则需把它施密特标准正交化: . 1 1 1 3 1 1 1 1 = = b b e 1 2 1 1 1 , 1 , 1 1 − = = 1 1 令b =

b,=a -a,eje =-a4A 2 6
− − = 1 1 1 3 1 1 1 1 − = 3 2 3 2 3 4 , 1 1 2 3 2 − = . 1 1 2 6 1 2 2 2 − = = b b e b e e 2 2 2 1 1 = − , 1 2 2 1 2 1 , b b b = −

于是得正交矩阵 1315 可以验知仍有 PAP=人. 由此可见,把一个方阵化成对角矩阵所用的正交变换矩 阵P不是唯一的
于是得正交矩阵 − − = 6 1 3 1 2 1 6 1 3 1 2 1 6 2 3 1 0 P 可以验知仍有 . T P AP = 由此可见,把一个方阵化成对角矩阵所用的正交变换矩 阵P不是唯一的

例2设矩阵 A= 10 矩阵B=(kE+A),其中k为实数,E为单位矩阵 求对角矩阵∧使B与∧相似,并求为何值时,B为奇异矩阵 解由 9 2-λ0 01-入 -1 =(2-入)}
例2 设矩阵 , 1 0 1 0 2 0 1 0 1 A = ( ) , , , 矩阵B = kE +A 2 其中k为实数 E为单位矩阵 求对角矩阵,使B与相似,并求k为何值时,B为奇异矩阵. 解 由 − − − − = 1 0 1 0 2 0 1 0 1 A E ( ) − − = − 1 1 1 1 2 (2 ) , 2 = −

可得A的特征值为入,=入2=2,入3=0 记对角矩阵 20 00 因为A为对称矩阵,故存在正交矩阵P,使PTAP=人 所以A=PP,于是 B=(&E+A}=(&PP+PAP月 = [p(kE+A)pT][p(kE+A)pT] =[p(kE+A)2 p"]
2, 0. 可得A的特征值为1 = 2 = 3 = 记对角矩阵 , 0 0 0 0 2 0 2 0 0 = , , . T 因为A为对称矩阵 故存在正交矩阵P 使P AP = 所以 A = PP T ,于是 ( ) ( ) 2 2 T T B = kE + A = kPP + PP = [ p(kE+Λ) p T ] [ p(kE+Λ) p T ] = [ p(kE+Λ)2 p T ]

(k+2) (k+2)月 由此可得 (k+2)月 (k+2) k2
由此可得 ( ) ( ) 2 2 2 2 P P 2 . + = + T k k k ( ) ( ) 2 2 2 2 2 . + = + k k k