
解n维单位坐标向量组构成的矩阵 E=(e,e2,,m 是n阶的单位矩阵。由E=1≠0,知R(E)=n,即R(E) 等于向量组中向量的个数,故由定理4知向量组是线性无 关的。 例2已知 试讨论向量组a1,a2,a3及向量组a1,a2的线性相关性
解 n维单位坐标向量组构成的矩阵 E = ( e1, e2,… , en ) 是 n 阶的单位矩阵。由 |E| = 1 ≠ 0,知R(E) = n ,即 R(E) 等于向量组中向量的个数,故由定理4知向量组是线性无 关的。 例2 已知 1 2 3 1 0 2 1 2 4 1 5 7 , , . = = = 试讨论向量组 α1,α2,α3 及向量组 α1,α2 的线性相关性

解对矩阵(a1,a2,a3)施行初等行变换,使之变 成行阶梯形矩阵,即可同时看出矩阵(a1,a2,a3)及矩阵 (a1,a2)的秩,由定理4即可得出结论。 a1,a2,a3)= 可见R(a1,a2,a3)=2,由定理4知向量组a1,a2,a3 线性相关;R(a1,a2)=2,向量组a1,a2线性无关
解 对矩阵( α1,α2,α3 )施行初等行变换,使之变 成行阶梯形矩阵,即可同时看出矩阵 (α1,α2,α3 ) 及矩阵 (α1,α2)的秩,由定理 4 即可得出结论。 (α1,α2,α3)= = 1 0 2 022 0 5 5 = 1 0 2 0 1 1 0 0 0 , 可见 R( α1,α2 ,α3 ) = 2,由定理4知向量组 α1 ,α2 ,α3 线性相关; R( α1,α2 )=2,向量组 α1 ,α2 线性无关。 1 0 2 1 2 4 1 5 7

例3已知向量组a1,a2,a线性无关,令P1=a1+a2, B2=a2+a,3=a3+a1,试证向量组邛1,B2,3线性无关。 证设有x1,32,x使 x1B1+x2p2+3B3=0, 即 xi(a1+a2)+x2(a2+a3)+x3(a3+a1)=0 亦即(x,+x3)a1+(x,+3)a2+(x3+x)a3=0 因a1,a2,a3线性无关,故有 x+x3=0 x+x2=0 x2+x3=0
例3 已知向量组α1 , α2 , α3线性无关 ,令 β1 = α1 + α2 , β2 = α2 + α3 , β3 = α3 + α1 ,试证向量组β1 , β2 , β3线性无关。 证 设有x1 , x2 , x3使 x1 β1+ x2 β2 +x3 β3 = 0, 即 x1 ( α1 + α2 ) + x2 ( α2 + α3 ) + x3 ( α3 + α1 ) = 0 亦即 ( x1 + x3 ) α1 + ( x1 + x2 ) α2 + ( x2 + x3 ) α3 = 0 因 α1 , α2 , α3 线性无关 ,故有 1 3 1 2 2 3 0 0 0 + = + = + = x x x x x x

由于此方程组的系数行列式 =2≠0 故方程组只有零解x=x2=x3=0,所以向量组阝1,2, 线性无关
由于此方程组的系数行列式 1 0 1 1 1 0 2 0 0 1 1 = 故方程组只有零解 x1= x2 = x3 = 0,所以向量组 β1 ,β2 ,β3 线性无关

定理5(1)若向量组Aa1,a2,,am线性相关,则 向量组Ba1,a2,,anm,anm+1也线性相关。反言之,若向量 组B线性无关,则向量组A也线性无关。 证:记A=(a1,a2,,am),B=(a1,42,,amat1)有 R(B)≤R(A)+1,若向量组A线性相关,则由定理4有R(4) <m,从而R(B)≤R(A)+1<m+1,再由定理4知向量组B线 性相关。 由上面的证明知:一个向量组若有线性相关的部分组, 则该向量组必线性相关。特别地,含有零向量的向量组一 定线性相关。一个向量组线性无关,则它的任何部分组都 线性无关
定理5 (1)若向量组 A: α1 ,α2 ,… , αm 线性相关,则 向量组 B :α1 , α2 ,…, αm , αm+1也线性相关。反言之,若向量 组 B 线性无关,则向量组 A 也线性无关。 证:记 A = ( α1 ,α2 ,… ,αm ) , B = ( α1 , α2 ,…,αm ,αm+1 ) 有 R(B) ≤ R(A) + 1 ,若向量组A线性相关,则由定理4有R(A) < m ,从而 R(B) ≤ R(A) + 1< m + 1,再由定理4知向量组 B 线 性相关。 由上面的证明知:一个向量组若有线性相关的部分组, 则该向量组必线性相关。特别地,含有零向量的向量组一 定线性相关。一个向量组线性无关,则它的任何部分组都 线性无关
(2)设 ?i=1,2,…,m) r+1 即向量a添上一个分量后得向量B,若向量Ag1,, 线性无关,则向量组B邛1B2,B也线性无关 反言之,若向量组B线性相关,则向量组A也线性相关 证记ArXm=(a1,a2,am),B+1)Xm=(f,B2,fm),看 RA)≤R(B).若向量组A线性无关,则RA)=m,从而R(B)≥n 但R(B)≤m,故R(B)=m,因此向量组B线性无关。 推论若维的向量线性无关,在维的向量组每个向量都 添上n-r个分量,得n维的向量组,则n维的向量组线性无关
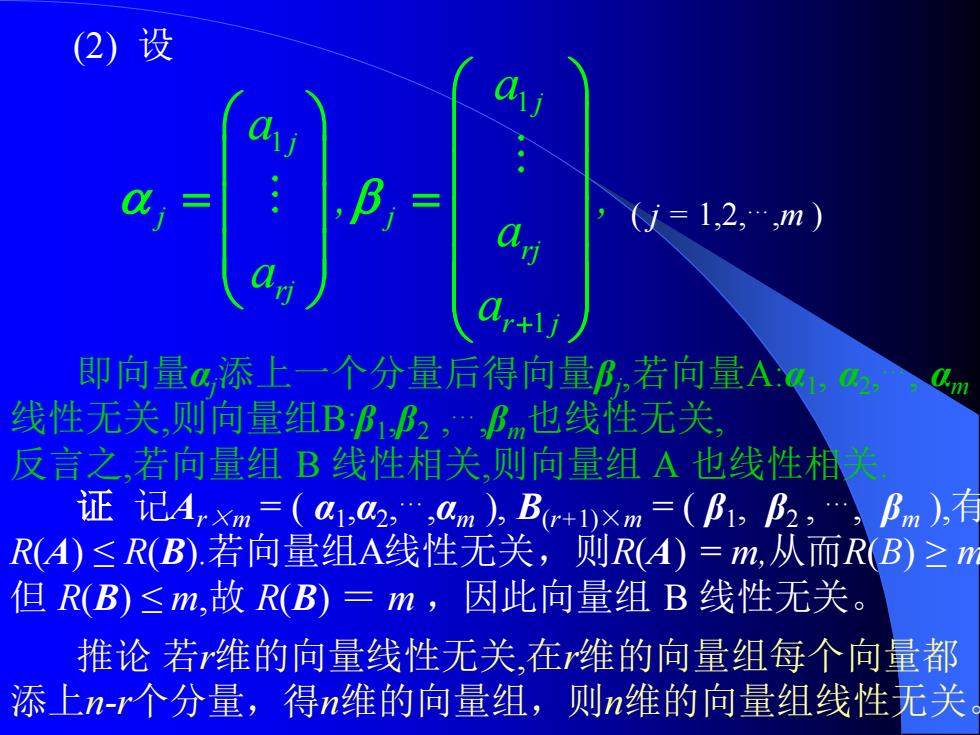
(2) 设 1 1 1 + = = j j j j rj rj r j a a , , a a a ( j = 1,2,…,m ) 即向量αj添上一个分量后得向量βj ,若向量A:α1 , α2 ,…, αm 线性无关,则向量组B:β1 ,β2 ,…,βm也线性无关, 反言之,若向量组 B 线性相关,则向量组 A 也线性相关. 证 记Ar×m = ( α1 ,α2 ,…,αm ), B(r+1)×m = ( β1 , β2 , …, βm ),有 R(A) ≤ R(B).若向量组A线性无关,则R(A) = m,从而R(B) ≥ m. 但 R(B) ≤ m,故 R(B) = m ,因此向量组 B 线性无关。 推论 若r维的向量线性无关,在r维的向量组每个向量都 添上n-r个分量,得n维的向量组,则n维的向量组线性无关

(3)m个n维向量组成的向量组,当维数n小于向量的 个数m时一定线性相关。 证m个n维向量a1,a2,,am构成的矩阵 Anxm=(a1:a2am), 有R(A)≤n. 若n<m,则R(A)<m,故m个向量a1,a2,,am线性相关
(3)m个n维向量组成的向量组,当维数n小于向量的 个数m时一定线性相关。 证 m个n维向量α1 ,α2 ,…,αm构成的矩阵 An×m = (α1 ,α2 ,…,αm), 有R(A) ≤ n. 若n < m,则R(A) < m,故m个向量α1 ,α2 ,…,αm线性相关

例4设有向量组aT=(a,a2,…,a,),(i=1,2,,m.m≤n) 试证向量组aT,a2T,",amT线性无关,其中a1,a2,,am为m 个互不相等且不等于零的常数。 证因为 a1T=(a1a2,am,,a1") a2T=(a2,a2a2m,,a2") amT=(amam2,amm,anm) 前m个分量作成的行列式 =aa2…am m-
例4 设有向量组αi T = (ai , ai 2 , … ,ai n ),(i = 1,2,…,m. m ≤ n ), 试证向量组α1 T ,α2 T ,…,αm T ,线性无关,其中a1 , a2 ,…, am 为m 个互不相等且不等于零的常数。 证 因为 α1 T = (a1 , a1 2 , … a1 m ,…,a1 n ) α2 T = (a2 , a2 2 , … a2 m ,…,a2 n ) αm T = (am, am 2 , … am m ,…,am n ) ……………………… ………… 前m个分量作成的行列式 1 2 2 2 2 1 2 1 2 m m m m m m a a a a a a a a a 1 2 1 2 1 1 1 1 2 1 1 1 m m m m m m a a a a a a a a a − − − =

=a4amΠ(a,-a)≠0 l≤j<ism 从而向量组 fT=(a1,a12,a1m) B2T=(a2,a22,a2m) Bm=(am amanm) 线性无关,所以增加分量后所得的向量组a1T,a2,,amT 线性无关
从而向量组 β1 T = (a1 , a1 2 , … a1 m) β2 T = (a2 , a2 2 , … a2 m) ……………………… βm T = (am, am 2 , … am m) 线性无关,所以增加分量后所得的向量组 α1 T , α2 T , …, αm T 线性无关。1 2 ( ) 1 m j i 0 j i m a a a a a = −

例5设A是nXm矩阵,B是mXn矩阵,其中n<m, 若AB=E,证明B的列向量线性无关。 证设B=(B1,P2…,Pn),其中P1,2,…,Pn是B的列 向量,若 x1B1+x22++xn阝n=0 即 (p,2,…,fn) BX=0 两边左乘A得ABX=0,即EX=0,从而X=0,所以 1,阝2,…,Pn线性无关
例5 设A是 n×m 矩阵,B是 m×n 矩阵,其中n<m, 若AB = E,证明B 的列向量线性无关。 证 设B = ( β1 , β2 , … , βn ),其中β1 , β2 , … , βn 是 B 的列 向量,若 x1 β1 + x2 β2 + … + xn βn = 0 即 ( β1 , β2 , … , βn ) = BX = 0 两边左乘 A得 ABX = 0 ,即 EX = 0,从而X = 0,所以 β1 , β2 , … , βn 线性无关。 1 2 n x x x