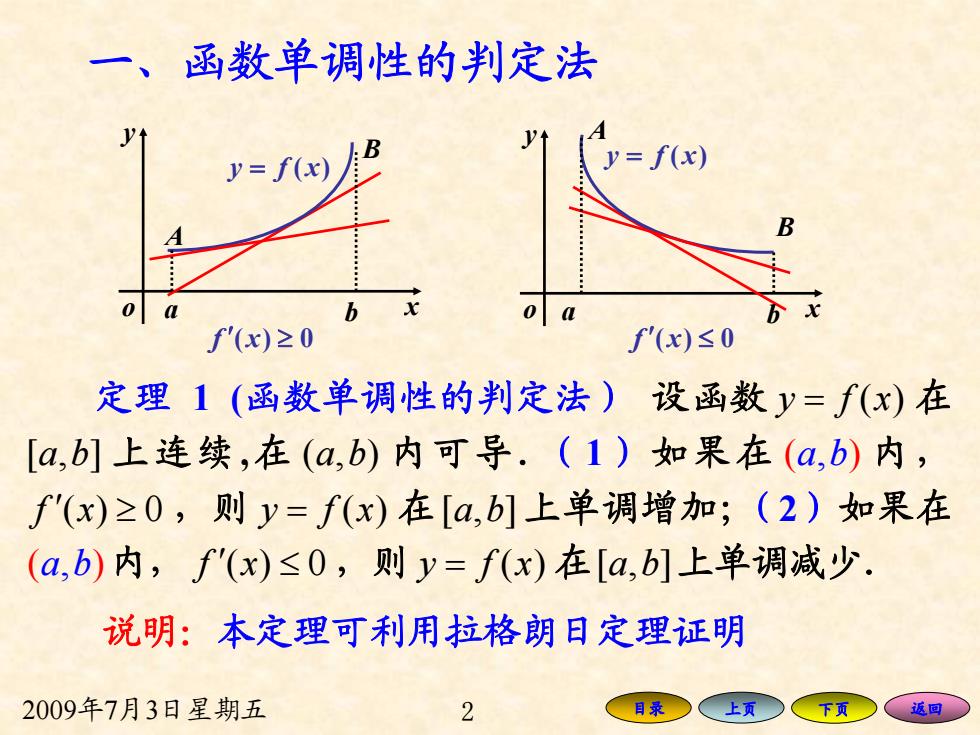
一、函数单调性的判定法 y=f(x) y=f(x) B 0 f'(x)≥0 f'(x)≤0 定理1（函数单调性的判定法）设函数y=f(x)在 [a,b]上连续，在(a,b)内可导.（1)如果在(a,b)内， f'(x)≥0，则y=f(x)在[a,b]上单调增加；（2)如果在 (a,b)内，f'(x)≤0，则y=f(x)在[a,b]上单调减少. 说明：本定理可利用拉格朗日定理证明 2009年7月3日星期五 2 目录 上页 返回 2009年7月3日星期五 2 目录 上页 下页 返回 一、函数单调性的判定法 定理 1 (函数单调性的判定法） 设函数 y fx = ( ) 在 [,] a b 上连续,在 (,) a b 内可导．（1）如果在 ( ) a b, 内， f x ′() 0 ≥ ，则 y fx = ( ) 在[,] a b 上单调增加；（2）如果在 ( ) a b, 内， f x ′() 0 ≤ ，则 y fx = ( ) 在[,] a b 上单调减少． x y o = fy x)( x y o = fy x)( a b A B f ′ x ≥ 0)( f ′ x ≤ 0)( a b B A 说明：本定理可利用拉格朗日定理证明